Design Cookbook: Climbing an Inclined Plane
Cookbook Index
Four Wheel Drive | Front Wheel Drive | Rear Wheel Drive | Step
Introduction:
This handout will examine the physics behind wheeled vehicles climbing slopes.
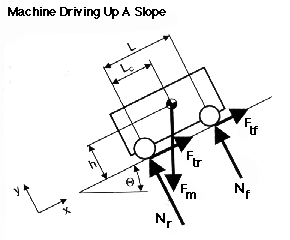
|
| Fm = mg |
(gravitational force of the machine) |
| Nf |
(normal force of both front wheels) |
| Nr |
(normal force of both rear wheels) |
| Ftf = Nf µ |
(tractional force of both front wheels, caused by static friction) |
| Ftr = Nr µ |
(tractional force of both rear wheels, caused by static friction) |
| L |
(distance between the front and rear wheels) |
| Lc |
(distance between the rear wheels and the center of mass) |
| h |
(height of the center of mass) |
| Ø |
(angle of incline plane) |
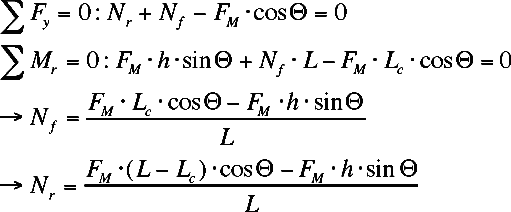
|
Tipping of the Machine occurs at h=hmax when Nf=0:
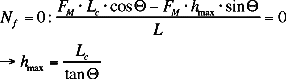
What can be done to prevent the machine from tipping?
- moving the center of gravity farther from the rear wheels
- decreasing the slope angle
Four Wheel Drive:
The necessary static coefficient of friction (µ4WD)
for a four wheel drive vehicle:
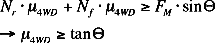
What can be changed to allow for a lower coefficient of friction?
- Decrease the slope of the angle
Front Wheel Drive:
The necessary static coefficient of friction (µFWD)
for a front wheel drive vehicle:
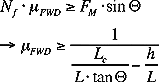
What can be changed to allow for a lower coefficient of friction?
- decrease the anlge of the incline
- move the center of gravity closer to the front wheels
- shortening the distance between the front and rear wheels
- lowering the height of the center of gravity
Rear Wheel Drive:
The necessary static coefficient of friction (µRWD)
for a rear wheel drive vehicle:
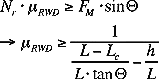
What can be changed to allow for a lower coefficient of friction?
- decrease the angle of the incline
- move the center of gravity closer to the rear wheels
- increasing the height of the center of gravity
A Wheel Driving Up a Step
|
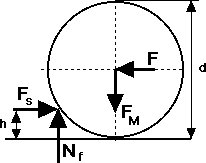
|
|
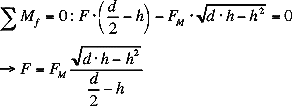 0
< h < d/2 0
< h < d/2
|

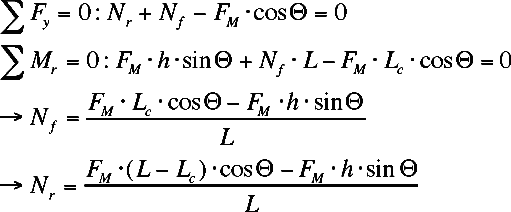
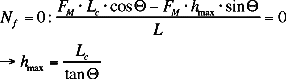
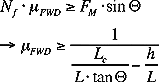
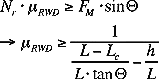

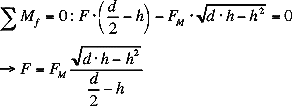 0
< h < d/2
0
< h < d/2