Calculation of the characteristics dune beam of cross section unspecified

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

1/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

Organization (S):

EDF-R & D/AMA, IAT St CYR, CS-SI

Manual of Reference
R3.08 booklet: Machine elements with average fiber
Document: R3.08.03

Calculation of the characteristics of a beam of section
unspecified transversal

Summary:

One presents the principle of the calculation of the various sizes characteristic of the sections of beams. Those
are established starting from the geometrical characteristics of the cross section of the beam.

These values are to be provided to the operand

SECTION: “GENERAL”

of the operator

AFFE

CARA

ELEM

[U4.42.01].

To determine them, of the numerical methods are presented, and implemented in the control

MACR_CARA_POUTRE

In the case of sections

“RIGHT-ANGLED”

and

“CIRCLE”

, one calculates directly in

AFFE_CARA_ELEM

characteristics using simplified formulas which one clarifies here.

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

3/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

Geometrical characteristics

Assumption:

One treats here only the cross sections of homogeneous and isotropic beams (same
material characteristics for all the points and in all the directions). The control

MACR_CARA_POUTRE

can also calculate the geometrical characteristics of a whole of sections

disjoined.

1.1 Section

unspecified

1.1.1 Principle

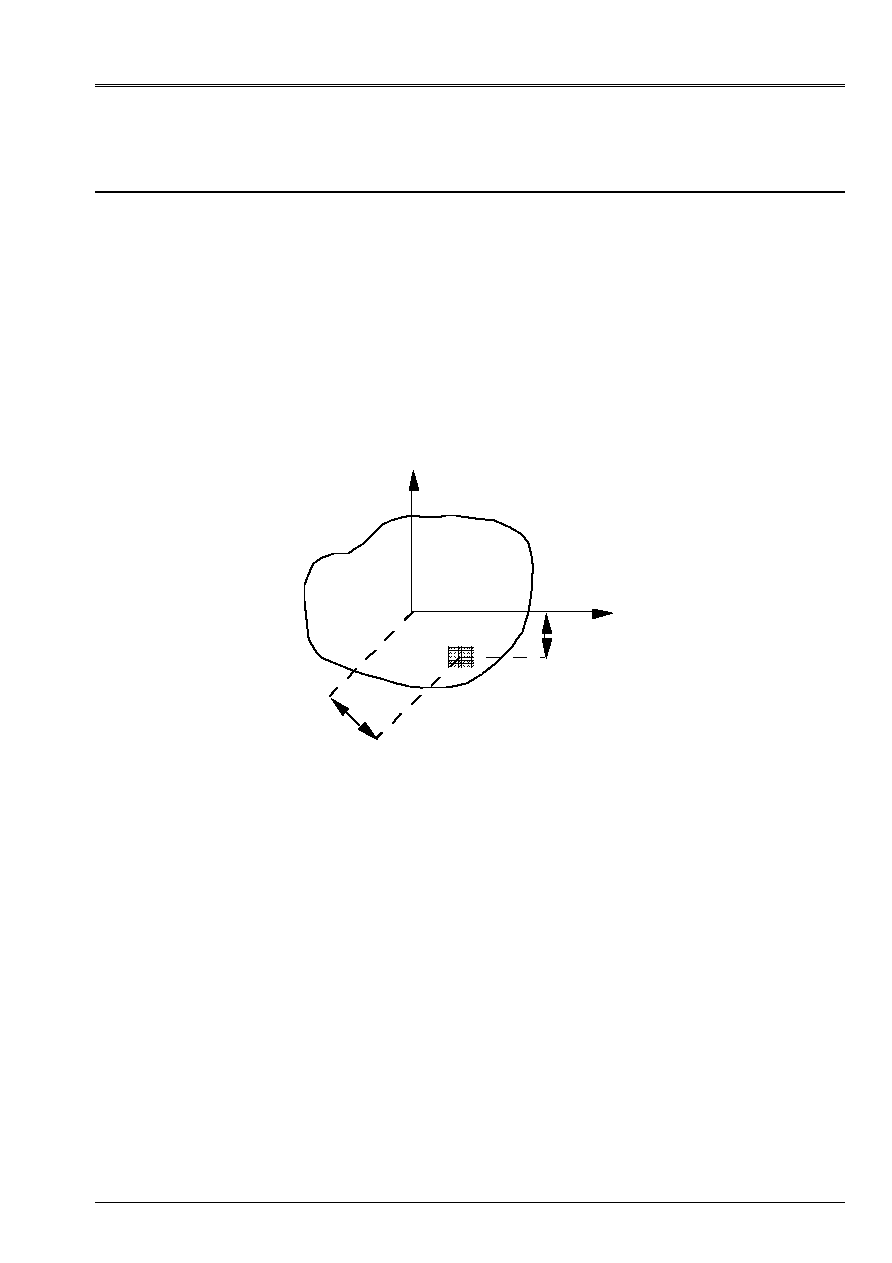
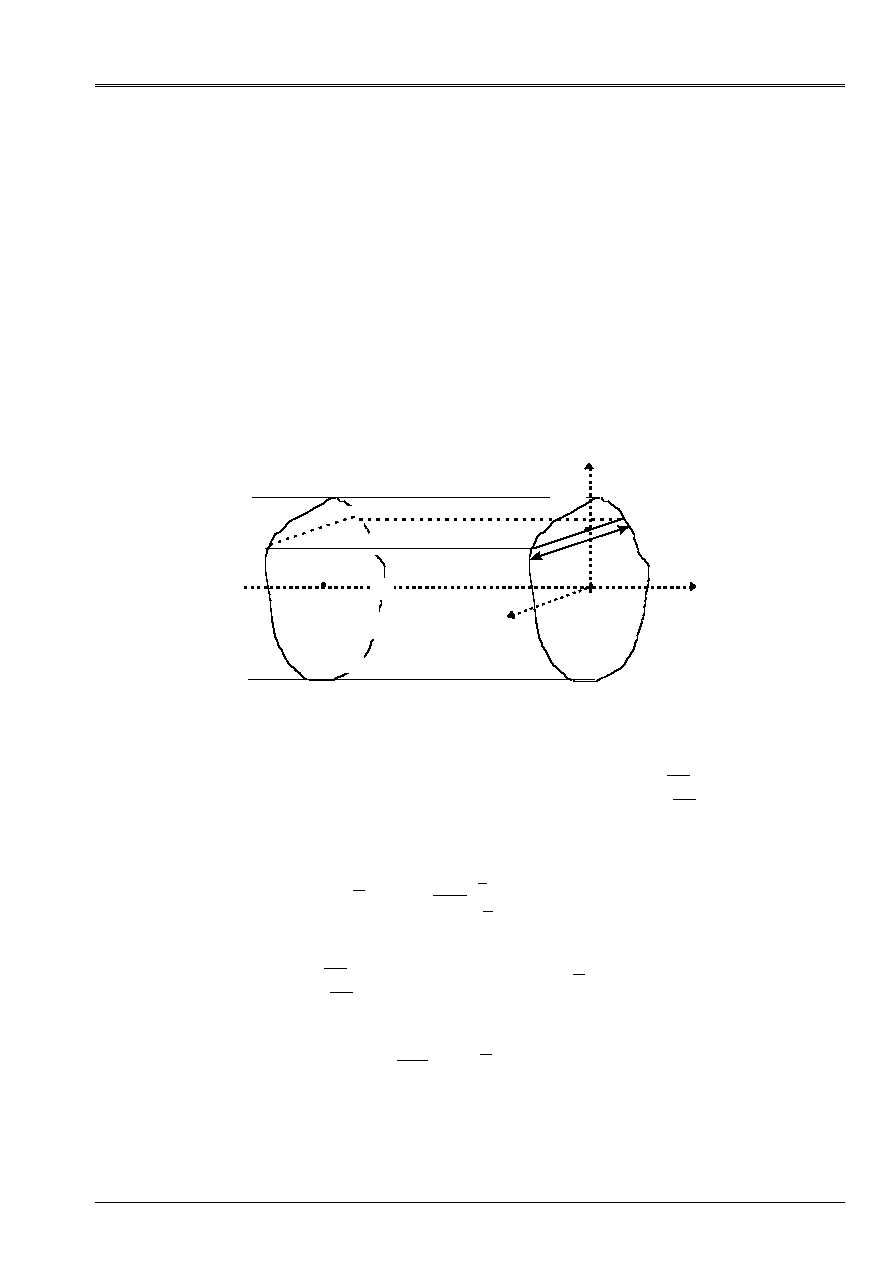
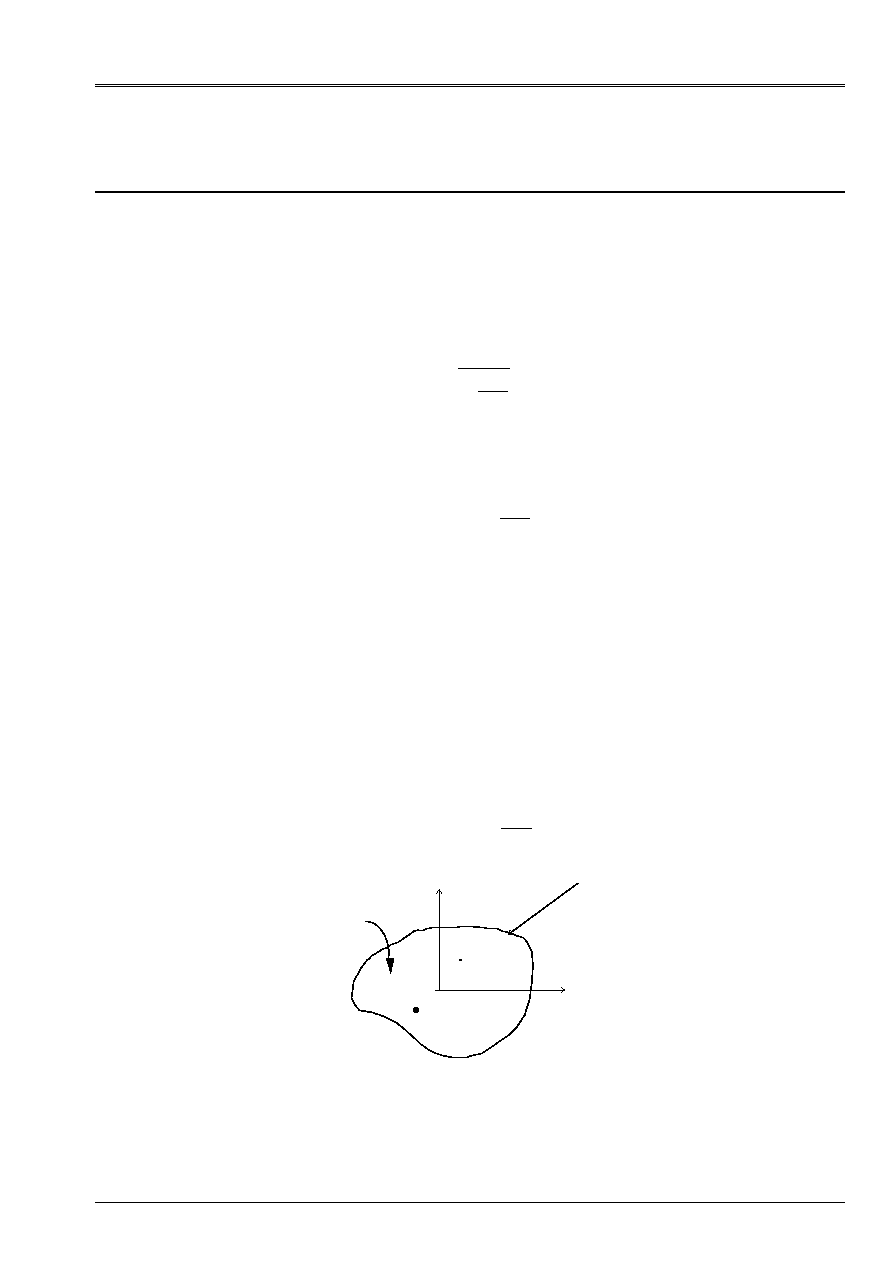
That is to say a section (S) of surface S in the plan (0, y, Z) whose origin O is the center of gravity G of
section, [Figure 1.1.1-a].

(S)

Appear 1.1.1-a: section in plan (0, y, Z)

Geometrical moment of inertia of (S) compared to the axis (OY) (which passes by the center of gravity)
express yourself by:

[]

Z dS

with

One defines in a similar way the geometrical moment compared to (O

) by:

y dS

When centrifugal geometrical moment (often called produced inertia of surface) defined by

y Z dS

is null, the axes (OY) and (O

) are main axes of the section (S). One

place for the continuation on this assumption;

and

are then called the geometrical moments

main.

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

4/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

Generally, we must place ourselves in the main axes of a section of beam
for all that relates to its characteristics since the elements of beam of Code_Aster are
formulated in this reference mark. On the basis of an origin located at the center of gravity, it is enough, to pass from one
unspecified system of axes (G, y', z') to the system of principal axes (G, y, Z), to carry out a rotation
of angle

such as [Figure 1.1.1-b]:

1
2

Arctg

y Z

(G, y, Z) main Axes

(G, y', z') unspecified Axes

Appear 1.1.1-b: main and unspecified Axes

The polar geometrical moment compared to the center of gravity is given by:

R dS

where R is the distance from the element dS in the center of gravity [Figure 1.1.1-a].

One deduces some naturally

= +

The polar geometrical moment intervenes in the calculation of the rigidity of torsion of the beams of section
circular (torsion of Coming Saint). For the other forms of sections, one will define a constant of
of the same torsion dimension.

Moreover, the geometrical moments can be calculated in another reference mark (P, y, Z), of origin P
unspecified different from the center of gravity G (formula of Huygens):

(

)

(

)

Z dS

GP.Z

(

)

(

)

y dS

GP. Y

GP.

(

) (

)

(

) (

)

yz dS

GP. Y GP.Z

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

5/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

in a general way, the formula of Huygens gives:

[]

(

) (

)

(

)

PG GM

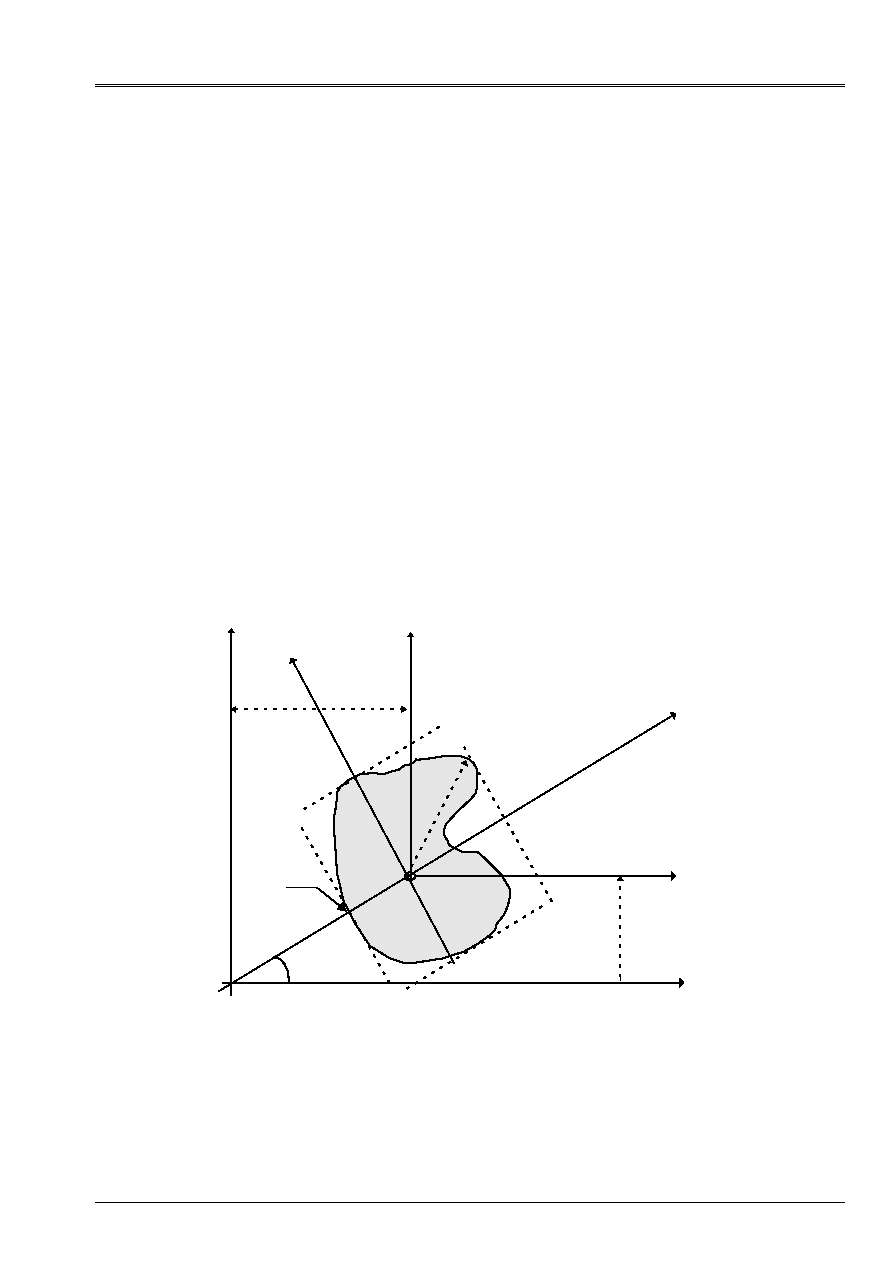
1.1.2 Calculation of the geometrical characteristics using

MACR_CARA_POUTRE

This macro-control allows the determination of the characteristics of a cross section of
beam starting from a mesh 2D of the section [U4.42.02]. It makes it possible to build a table of
values, usable in the control

AFFE_CARA_ELEM

(

SECTION

“GENERAL”

[U4.42.01]).

The geometrical characteristics can be calculated on the complete mesh, half mesh with
symmetry compared to X or with Y, quarter of mesh with two symmetries compared to X and with Y
[Figure 1.1.2-a].
These characteristics are calculated in the table for all the mesh and each group of
meshs of the list specified by the user (case of a network of beams).

The data correspond to a half or a quarter of the section if the key words

SYME_X

SYME_Y

are present.

Z_MIN

y (main)

R_MAX

Z_MAX

ALPHA

CDG_Y

CDG_X

Z (main)

Y_MIN

Y_MAX

Appear 1.1.2-a: Definition of the geometrical characteristics

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

6/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

The results are gathered in four groups:

1) In the reference mark

OXY

of description of the mesh 2D for the mesh provided by the user

surface:

AIRE_M

position of the center of gravity:

CDG_X_M,

CDG_Y_M

moments and product of inertia of surface, in the center of gravity

in the reference mark

GXY

IX_G_M

IY_G_M

IXY_G_M

2) In the same total reference mark, for the mesh obtained by symmetrization if

SYME_X

SYME_Y

surface:

SURFACE

position of the center of gravity:

CDG_X,

CDG_Y

moments and product of inertia of surface, in the center of gravity

in the reference mark

GXY

IX_G

IY_G

IXY_G

3) In the main reference mark of inertia

Gyz

. cross-section, whose denomination corresponds to that

used with the description of the elements of neutral fiber beam

[U4.24.01].

main moments of inertia of surface in the reference mark

Gyz

, usable for the calculation of rigidity

of bending of the beam:

IY_PRIN_G

and

IZ_PRIN_G

angle of flow of the reference mark

GXY

with the main reference mark of inertia

Gyz

ALPHA

characteristic distances, compared to the center of gravity

section for calculations of

maximum stresses:

Y_MAX

Y_MIN

Z_MAX

Z_MIN

and

R_MAX

4) In the total reference mark, in a point P provided by the user:

X_P

Y_P

: not calculation of the moments of inertia

IX_P

IY_P

IXY_P

: moments of inertia in the reference mark

PXY

IY_PRIN_P

IZ_PRIN_P

: moments of inertia in the reference mark

Pyz

1.1.3 Calculations

carried out

The list of the controls called by

MACR_CARA_POUTRE

is indicated in the document [U4.42.02].

The preceding quantities are obtained by the call to

POST_ELEM

, for the option

“CARA_GEOM”

. Of

more, one can add the key words to it

SYME_X

SYME_Y

, and

ORIG_INER

who defines the P. point.

Calculations are carried out in

POST_ELEM

, for all the mesh, then possibly for each

group meshs, in the following way:

1) Loop on the elements 2D (modeling

D_PLAN

), with call of the elementary option

“MASS_INER”

. One is obtained

CHAM_ELEM

with a value by element (1 point of Gauss)

containing the components:

element

y dS

, xy

2) Summation of the preceding elementary quantities to obtain:

AIRE_M

CDG_X_M

CDG_Y_M

IX_G_M

IY_G_M

IXY_G_M

3) Calculation

SURFACE

CDG_X

CDG_Y

IX_G

IY_G

IXY_G

(taking into account of

SYME_X

SYME_Y

)

4) Calculation

IY_PRIN_G

IZ_PRIN_G

ALPHA

5) Calculation

Y_MAX

Z_MAX

Y_MIN

Z_MIN

R_MAX

6) If one clarifies a point P particular (key word

ORIG_INER

), one calculates also the characteristics

in the total reference mark of origin P:

PXY

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

7/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

1.1.4 Examples

of use

: Full rectangle (treaty by test ZZZZ105G)

GR2

GR1

B = 0.01

H = 0.025

Geometrical characteristics obtained

PLACE AIRE_M

CDG_X_M

CDG_Y_M

IX_G_M

IY_G_M

IXY_G_M

0.000003

1.00E-03

4.24E-18

- 3.39E-18

2.08E-07

3.33E-08

2.65E-23

GR1

5.00E-04

2.20E-17 - 1.25E-02 2.60E-08

1.67E-08

3.97E-23

GR2

5.00E-04

- 8.47E-18 1.25E-02

2.60E-08

1.67E-08

5.62E-23

PLACE

SURFACE

CDG_X CDG_Y IX_G IY_G IXY_G IY_PRIN_G IZ_PRIN_G ALPHA

0.000003 1.00E-03 4.24E-18 - 3.39E-18 2.08E-07 3.33E-08 2.65E-23 3.33E-08 2.08E-07 9.00E+01
GR1

5.00E-04 2.20E-17 - 1.25E-02 2.60E-08 1.67E-08 3.97E-23 1.67E-08 2.60E-08 9.00E+01

GR2

5.00E-04 - 8.47E-18 1.25E-02 2.60E-08 1.67E-08 5.62E-23 1.67E-08 2.60E-08 9.00E+01

PLACE X_P

Y_P IX_P

IY_P

IXY_P

IY_PRIN_P

IZ_PRIN_P

0.000003

0.00E+00 0.00E+00

2.08E-07 3.33E-08

2.65E-23

3.33E-08

2.08E-07

GR1

0.00E+00 0.00E+00

1.04E-07 1.67E-08

- 9.79E-23

1.67E-08

1.04E-07

GR2

0.00E+00 0.00E+00

1.04E-07 1.67E-08

3.31E-24

1.67E-08

1.04E-07

PLACE Y_MAX Z_MAX Y_MIN Z_MIN R_MAX
0.000003

2.50E-02

1.00E-02

- 2.50E-02

1.00E-02

2.69E-02

GR1

1.25E-02

1.00E-02 1.25E-02

1.00E-02

3.36E-02

GR2

- 1.25E-02 - 1.00E-02 - 1.25E-02 - 1.00E-02 3.36E-02

1.2

Particular case of the sections rectangular and circular

The geometrical characteristics are directly calculated in

AFFE_CARA_ELEM

from

data of the user.

epz

epy

Appear rectangular 1.2-a: section

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of unspecified cross section

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

8/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

In the case of the rectangular beam (Operand

SECTION: “RIGHT-ANGLED”

), calculation gives:

(

)

(

)

[

]

= 1

H H

(

)

(

)

H H

Appear circular 1.2-b: section

For the circular section (Operand

SECTION:

“CIRCLE”

), one obtains:

(

)

[

]

(

)

[

]

= =

Coefficients of shearing and the center of shearing

It is a question of evaluating the coefficients

With

intervening in the models of beams of

Timoshenko with taking into account of the shearing strains. For the beams of EULER, these
coefficients do not intervene [U4.42.01 §7.4.2] and [R3.08.01 §2.3.1]. These coefficients are obtained
for a linear elastic behavior.

In the case of the unspecified sections, the coefficients of shearing are to be provided by the user
in

AFFE_CARA_ELEM

, if the selected element is a beam of TIMOSHENKO (model

POU_D_T

POU_C_T

POU_D_TG

and

POU_D_TG_M

In the case of the circular or rectangular sections, the coefficients of shearing are calculated
by analytical methods of [§2.1].

In all the cases, they can be calculated by

MACR_CARA_POUTRE

, starting from the plane mesh of

section. The numerical method used is exposed to [§2.3]. This method applies to
unspecified sections (of homogeneous and isotropic material). In appendix 2, one describes an extension of
this method with the case of a network of parallel beams maintained between two rigid floors.

The position of the center of torsion (or shearing centers) is obtained only by methods
numerical (cf [§2.3]). For the rectangular and circular sections, as for all the sections
in 2 symmetry planes, the center of torsion is confused with the center of gravity of the section.

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

9/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

2.1 Methods

analytical

One describes three analytical methods allowing to calculate coefficients of shearing,
applicable to the unspecified sections.
The first two methods differ by the definition which they propose of the coefficient of
shearing, but rest on the same assumption which consists in postulating the form of the distribution
shear stresses in the section.

2.1.1 Assumption of distribution of shearings: formulate JOURAWSKI

Let us consider for example the case of a beam of cross-section S, subjected to a sharp effort

. One writes the balance of a prismatic part of the beam, ranging between the sections

straight lines

and

x+a

and between the plan of cut located at the ordinate

and

max

(ref. [bib8]). Efforts

acting on this part of beam are the vectors forced on the faces

and

x+a

, and those

acting on the face located in

x+a

max

x+a

B (Z)

Appear 2.1.1-a

By applying the theorem of the resultant, one obtains:

(

)

(

)

(

) ()

(

)

X has

X has

B y

X y Z Dy dz

NR X has y

NR X y

y Z D dz

()

To evaluate the term of straight line, JOURAWSKI proposed to consider only the average of
shearings according to Z:

() ()

(

)

X y

B y

X y Z dz

then

(

)

()

B y

X has

y Z D dz

B y

y D

()

and while making tend has towards 0,

() ()

B y

X y

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

10/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

The equilibrium equations of beam and the distribution of bending stresses (in elasticity) give:

()

(

)

NR X y

X y Z dydz

M X y

dydz

().

()

M X

m y

T B T dt

() ()

()

with

max

thus

()

X, y

m y

I B y

m y

I B y V

()

The distribution of shearings according to

is thus given by the formula of JOURAWSKI:

()

X, y

m y

I B y V

m y

T B T dt

()

with

max

éq

2.1.1-1

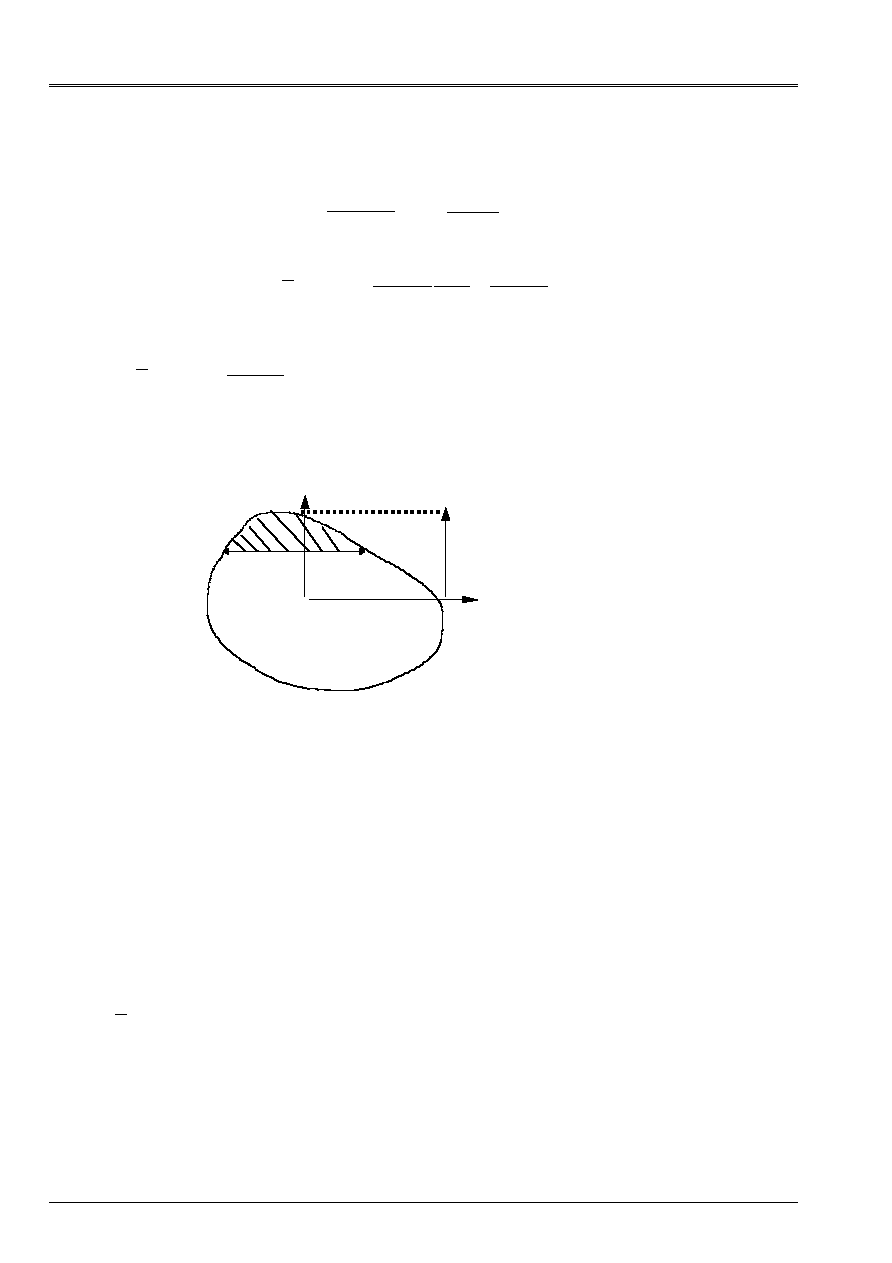
in accordance with [U4.24.01], with the notations of [Figure 2.1.1-b]. Quantity

()

m y

represent it

static moment on behalf of section (hatched) included/understood enters

and

max

B (y)

max

()

m y

y Dy dz

Appear 2.1.1-b: section of beam

This distribution checks the boundary conditions well following three-dimensional problem there:
shearing is quite null on bottom fibers and higher (

min

, or

max

). But it

account holds that average of shearings according to Z.

By applying this formula to a full rectangular section, one finds a distribution parabolic
according to Y. By applying it to a beam of circular section, one finds a distribution parabolic in y
and in Z, which varies more slowly according to Z than according to Y.

This remains valid for the other full sections. For sections comprising of the holes, it is necessary
to take guard to consider only the matter in the calculation of

B y

()

2.1.2 Method of TIMOSHENKO

With the origin, TIMOSHENKO (ref. [bib9]) proposed a simple definition of the coefficient of shearing,
as being the relationship between the transverse shear stress average in the noted section

and its maximum value

(

)

CT max

Owing to the fact that we always have the shearing action by:

éq

2.1.2-1

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

11/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

we deduce:

Knowing that TIMOSHENKO proposes to write:

Max

éq

2.1.2-2

to determine

, it is enough to express the sharp effort

[éq 2.1.2-1] according to

Max

. In the general case of the unspecified sections, there will be naturally two coefficients

and

, for each of the two main axes.

It remains to determine

Max

. For that, TIMOSHENKO makes an assumption on the distribution of

stresses shear transverse: the transverse shear stress has a distribution
parabolic in the direction of the shearing action which produces it, with its maximum value in the center and
zero values at the edges. This is true according to the formula of JOURAWSKI for a section
rectangular. By extension, the method extends this assumption of parabolic distribution to one
unspecified section

This method is not applied in Code_Aster, except for the hollow rectangular sections.
One uses the following method in the other cases.

2.1.3 Method

“energy”

Actually, the definition suggested by TIMOSHENKO proves little used in practice today; one him
prefer a formulation based on internal energy due to shearing in the section. The aforementioned is written:

1
2

where

is the modulus of rigidity (equal to

The new definition of the coefficient of shearing is sometimes allotted to MINDLIN and is expressed by:

K SG

1
2

éq

2.1.3-1

So by substitution, one thus defines for a homogeneous material section the coefficient of
shearing by:

[

]

éq

2.1.3-2

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

12/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

By making an assumption on the distribution of stress in the section, one can thus estimate
value of

. From the formula of JOURAWSKI [éq 2.1.1-1], the preceding expression can be written

(ref. [bib5]):

y dS

()

éq

2.1.3-3

2.1.4 Method of COWPER

One can also take into account the three-dimensional effects to determine the coefficient

;

various formulations were proposed, by COWPER [bib3] and were taken again in particular by BLEVINS
[bib2], while being based on the resolution of the three-dimensional problem of Saint-Coming.

In this case, the coefficient

is a function of the Poisson's ratio, in general one

approximation with the first command. COWPER uses the three-dimensional equations of elasticity in
the dynamic case to propose an expression of

giving good results in statics and in

low frequency dynamics. The approximation which makes it possible to lead to the formula suggested consists with
to consider a distribution of not parabolic stress, but resulting from the static problem
(solved analytically) of the beam cantilever transversely charged at its loose lead. It is with
to note that the distribution obtained is strictly identical to the problem with a transverse loading
uniformly distributed.

2.2

Particular case of the sections rectangular and circular

One distinguishes the full beams and the tubes.

For the full rectangular section, the coefficient of shearing is determined by the method based
on energy shearing with parabolic distribution of the stresses interns

()

[éq 2.1.3-3]. Applied to the rectangular section, one obtains

= = 56

. It should be noted that this value also corresponds to the method of COWPER when

the Poisson's ratio is taken equal to zero.

For the rectangular tube, Code_Aster uses the method of TIMOSHENKO which leads to

= = 23

In the case of the beams with full circular section, one uses the energy method which leads to

= = 9

. This value is also obtained by the method of COWPER when it

Poisson's ratio is equal to

1
2

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

13/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

For the circular tubes, one distinguishes the tubes with fine wall and those with thick wall. If one notes

the report/ratio of the internal radius to the external radius, a tube is with fine wall when m

0.9, if not

it is with thick wall.

The coefficient of shearing of the circular tube with fine wall is given by the method of COWPER, in

considering that m = 1 and for a null Poisson's ratio, is

= = 12

For the circular tubes with thick wall, one uses an approximate formula of the method of
COWPER which is written:

1 093

0 634

1156

0 905

Let us notice that this formula does not ensure continuity with the borderline cases of the full cylinder (m = 0)
and of the cylinder with infinitely thin wall (m = 1).

If preceding choices (carried out by

AFFE_CARA_ELEM

in the case of circular sections and

rectangular) are not appropriate, it is always possible to calculate the coefficients numerically
of shearing using

MACR_CARA_POUTRE

, the method is specified in the § according to.

2.3 Numerical method of calculation of the coefficients of shearing and of

center shearing

2.3.1 Calculation of the coefficients of shearing:

This method takes as a starting point the the ref. [bib1], page 62. It allows the simultaneous determination of
constants of shearing and the center of torsion. It is implemented in

MACR_CARA_POUTRE

starting from a plane mesh of the section. It functions currently only for sections
homogeneous and isotropic (for nonhomogeneous sections, the method is similar [bib1] but not
available in Code_Aster).

As for the energy method, one compares for a sharp effort

internal energy

had with shearing in the section with energy U

associated the model of MINDLIN:

dS U

K SG

1
2

The coefficient of shearing is expressed by:

SGU

= 12

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

14/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

U thus should be calculated

and thus shear stresses (in elasticity) in the section for

to estimate the value of K .On is placed in the main reference mark of inertia (G, y, Z), and one supposes that
beam is subjected only to one sharp effort

. It results from it that:

()

Z M X

Z VI

The equilibrium equations make it possible to write:

Z VI

= =

In addition, the kinematics of the beam in bending/shearing is:

(

)

()

(

)

(

)

()

U X y Z

U X

U y Z

v X y Z

W X y Z

W X

()

U y Z

representing axial displacement due to the roll of the section. Deformations

are written:

()

U X

U y Z

W X

By using the relation of behavior of linear elasticity, the stresses are written:

()

U y Z

W X

The components of shearing thus check:

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

15/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

This relation makes it possible to introduce the function of stresses

such as shear stresses

in the section are written:

The equilibrium equation then makes it possible to obtain the function

by resolution of a problem

quasi-harmonic which is written:

G N

+ =

with

in a point

This makes it possible to calculate

then shearings. In practice, in

MACR_CARA_POUTRE

, one uses

THER_LINEAIRE

to solve the problem, while assimilating

at the temperature. One chooses

=1 and

G=1 (G does not intervene any more in the expression of the coefficient of shearing). Boundary conditions of
this problem of stationary thermics are:

source F being worth

null flow on

null temperature in a point of

One can then determine

()

1
2

by a calculation

elementary on all the elements of the section, with the option

“CARA_CISA”

(calculation of the gradient), then

summation on these elements. One calculates then

= 12

SGU

Same calculation is carried out with

to determine

= 12

SGU

The provided result is

With

2.3.2 Calculation of the co-ordinates of the center of shearing

The center of shearing C is the point of the section where shear stresses due to an effort
edge generate one null torque. This point is also called center of torsion, because it
remain fixed when the section is only subjected to one torque.

The torque compared to the point G is worth:

(

)

Z dS

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

16/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

The torque compared to the point C sought is:

(

)

(

)

(

)

y y

Z Z dS

Z V

C y

teststemxç

To determine the co-ordinates of the center of shearing, preceding calculation is used [bib1]:
From the shear stresses determined for

=1 and

=0, one calculates

(

)

Z dS

One obtains:

For

=1 and

=0, one obtains:

= -

= -

2.3.3 Example

Let us take again the example of the rectangular section [§1.1.4].

GR2

GR1

B = 0.01

H = 0.025

The coefficients of shearing obtained are identical to the analytical value (6/5).

PLACE AY AZ EY

all 1.20E+00 1.20E+00 8.72E-19 3.16E18

Co-ordinates of the center of torsion EY and EZ (in the reference mark main (G, y, Z)) are null:
center shearing/torsion is actually confused with the center of gravity.

2.4

Calculation of the coefficients of shearing of a network

The method described in appendix 2 makes it possible to calculate coefficients of shearing of a beam
equivalent to a whole of parallel beams embedded on a rigid floor and embedded or
rotulées on another.

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

17/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

Constants related to torsion

The constant of noted torsion

must allow to take account of the roll of the sections

straight lines (not circulars) at the time of a deformation in torsion. It is used in the models of beams
straight lines treated by Aster (EULER, TIMOSHENKO and warped TIMOSHENKO or

POU_D_E

POU_D_T

POU_C_T

and

POU_D_TG

). In the case of the circular sections, the sections are not warped and

constant of torsion is equal to the polar geometrical moment

. The constant of torsion C is

defined as the moment necessary to produce a rotation of 1

radian per unit of length

divided by the modulus of rigidity, that is to say:

éq 3-1

with the same dimension as the geometrical moments of inertia

and

that is to say

For a circular section, the definition [éq 3-1] is coherent since we have:

Determination of

in the general case is made in a numerical way (

MACR_CARA_POUTRE

) and

tiny room to a calculation of Laplacian in 2D. The method presented here is detailed in the ref. [bib1] [§3.6.3]
for the simply related sections. An original method for calculation of the constants of
torsion with perforated sections is detailed in appendix. The results here are given.

3.1

Calculation of C in the case of unspecified sections

The complete resolution of the problem is in appendix. One gives here simply the results.

According to the assumptions of the theory of the pure torsion of Saint-Coming, there is no deformation of
the average line and not of lengthening along the longitudinal axis. Torsion is free, i.e.
that it does not generate axial stresses. In other words, the sections can warp
freely. If one remains in small displacements, one admits that the swing angle of the cross-sections
is worth:

()

X X

X =

éq

3.1-1

(S)

(

)

M (y, Z)

Appear 3.1-a

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

18/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

If the point C is the center of torsion (which by definition remains motionless when the beam is subjected to
a torsion), the field of displacement

()

U M

is given by [bib1]:

()

(

)

(

)

()

U
v

X X

y y

Z Z

y Z

-
-

0
0

()

(

)

(

)

y Z

X X Z Z

X X there y

where

()

y Z

is related to roll.

The law of HOOKE is written:

(

)

()

Trace

where

is the matrix unit and the tensor of the deformations is worth

(

)

() +

()

1
2 grad

grad

By neglecting the terms of the second command, in

2 X

, one leads to:

éq

3.1-2

One posed:

()

y Z

function of stress. It is noted that the relation of balance

div

is then

checked.

While deriving, one obtains:

Z y

y Z

By adding the two equations, one leads to:

= -

éq 3.1-3

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

19/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

It remains to establish the boundary conditions. One notes

the normal directed towards outside at the border

(

) which can be multiplement related:

Without external loading, one must have

N 0

, which can be written

Z N

y N

0
0

where

and

are the two components of the normal.

This writing can be thus put in the form

grad

who implies that the vectors

and

grad

are colinéaires. It thus follows that

()

y Z

is constant on each related component

border (

). One can impose for example that

()

y Z

that is to say null on external contour:

If the sections behavior of the holes, constants

are unspecified. For

to allow the resolution of the complete problem, it is necessary to add equations. Those are obtained with
to leave the circulation of the function of roll on each closed contour. They are obtained
following conditions:

()

N DLL

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

20/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

where

()

is the surface surrounded by the border

()

. These conditions are brought back to conditions

conventional of imposed flow (where

()

represent the length of the border

()

Finally, the problem to be solved is written:

= -

()

Once solved this problem, one obtains the constant of torsion by:

()

3.2

Calculation of the constant of torsion in

MACR_CARA_POUTRE

This calculation is carried out in

MACR_CARA_POUTRE

by the resolution of a problem of thermics. It is necessary

for that that the user specifies with

MACR_CARA_POUTRE

the group of mesh which defines the edge

outside, and if the section comprises holes, groups of meshs which define the contour of
each one of them.
One solves a linear problem of thermics then (

THER_LINEAIRE

) on a plane mesh of

section to find the function

. One places oneself first of all in the main reference mark of inertia

(

CREA_MAILLAGE

), starting from the co-ordinates of the center of gravity and the orientation of the main reference mark

calculated previously.

One defines then the boundary conditions in

AFFE_CHAR_THER

The source term is worth 2

The temperature of the external edge is imposed and is worth 0 (

TEMP_IMPO

)

And if the section comprises holes (presence of one or more groups of meshs them
defining):
- On each group of mesh defining a hole, the temperature is constant

(

TEMP_UNIF

)

Flow is worth 2 times the surface of the hole divided by the length of its edge. These quantities are
calculated before.

The calculation of C is carried out in

POST_ELEM

by the key word

CARA_TORSION

key word factor

CARA_POUTRE

. In this case, one calculates on each element the integral of

, (option

CARA_TORSION

on the plane thermal elements), then one carries out the sum on all them

elements.

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

21/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

Example:

Still let us take again the example of the rectangular section [§1.1.4].

The coefficients of shearing obtained are:

PLACE

CT [éq 3.3.2] CT (Aster)

all 9.9805E-08

9.9681E-08

3.3

Calculation of the radius of torsion in an unspecified section

The radius of torsion is calculated thanks to the calculation of the function of stresses on the mesh of
section. Rt is added in the table produced by

MACR_CARA_POUTRE

[U4.42.02].

The resolution of a stationary thermal problem of unknown factor

allows to determine the constant

of torsion and stresses shear.
The determination of the radius of Rt torsion is the resolution of:

Rt = grad (

) .n

(or N represents the normal vector external with the edge considered of the section)

Rt varies along external contour; indeed, for an unspecified section, shearings due to
torsion vary on the edge. One chooses to take the value of Rt leading to shearings
maximum on the external edge, i.e. the maximum value of Rt (in absolute value) on contour
external.

Moreover, if the section is alveolate, there are several “several radii of torsion”: Rt = 2 * A (K)/L (K) (or
With (K) represents the surface of the cell K and L (K) its perimeter). If one is satisfied to seek the value
maximum of shearing, it is necessary to take the maximum of the Rt values obtained on the external edge and
on the cells.

The radius of torsion is given in

MACR_CARA_POUTRE

only by controls

python. During the unfolding of

MACR_CARA_POUTRE

the control

POST_ELEM

is called, one

new parameter RT is thus created for this control.

3.4

Constant of torsion of the sections circular and rectangular

Expressions simplified for these two types of sections are described here. The calculation of
constants of torsion is then directly carried out in

AFFE_CARA_ELEM

For the circular section the preceding expressions remain valid. By taking a function of

torsion of the form

()

(

)

y Z

1
2

one finds indeed:

(

)

For the rectangular section, calculation is naturally more complex but can be carried out in
choosing a function which is cancelled indeed at the edges, of the form:

()

(

)

(

)

, =

y Z

With

2 1

cos

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

22/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

The resolution involves with a constant of torsion which is written:

C hh

H H

éq

3.4-1

where

C hh

express yourself in the form of a series which takes the following values:

C hh

0.281 0.286 0.299 0.312 1 3

In fact, Code_Aster employs a formula simplified (ref. [bib1]) for the full rectangular section
who is written:

H H

3 36

0 280

éq

3.4-2

It is valid if

; in the other case it is enough to exchange the respective places of

and

agreement between the two expressions is very good as indicates it the following table:

1 2 4 8

H H

according to [éq 3.3-1]

0,1405

0,2288

0,2814

0,3072

1/3

H H

according to Aster [éq 3.3-2]

0,1408

0,2289

0,2809

0,3071

1/3

For the hollow rectangular beam, there is an approximate solution which is written (ref. [bib2] and [bib6]):

(

)

(

)

ep ep H

H ep

with the notations of [Figure 1.2-a]: section in plan (0, y, Z).

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

23/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

3.5

The effective radius of torsion

The effective radius of torsion

allows to calculate the transverse shear stress of torsion

maximum

according to the torque. One will be able to consult on this subject the drafting of

MASSONET on this aspect (ref. [bib5]). We have as follows:

MR. RC

In the case of circular cylinders,

is equal to the radius (external if it is a tube) of the section.

For the rectangular sections, the problem is definitely more complex. Code_Aster imposes it
radius of torsion of the full section by:

(

)

4 3

This approximate expression remains valid if the beam is not flattened too much. DHATT and BATOZ
(ref. [bib1]) give an expression having a field of validity more extended, but actually it acts
in any rigor of a series whose numerical values are given by MASSONET (ref. [bib5]).

For the hollow rectangular beam, Code_Aster imposes an expression which is valid only if
wall is thin and constant thickness

, that is to say:

(

)

(

)

ep H

It is about a “adaptation” of the formula:

E With

where

is the thickness of the wall (constant) and

With

the surface contained inside the average line.

This last expression is known under the name of first formula of BREDT (cf ref. [bib1] and
[bib5]).

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

24/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

Calculation of the constant of roll

The constant of roll is used by the model of beam with roll
(modeling

POU_D_TG

and

POU_D_TGM

), that it is important to take into account for the beams with

open mean sections (cf [R3.08.04]).

This coefficient (noted

in [R3.08.04]) intervenes in the expression of the virtual work of the efforts

interiors on the terms of torsion:

(

)

E I

X X

X xx

int

express yourself in the same unit as the geometrical moments of inertia

that is to say

By taking again the approach of [§3.1], and while placing itself in a reference mark related to the center of torsion C,
kinematics of the torsion of an unspecified section is:

()

U
v

X X

X
y
Z

y Z

0
0

()

y Z

X X Z

X X y

where

()

y Z

is related to roll (which cancels only in the case of a section

circular).

The expression of the stress field is (in elasticity):

()

E y Z

y Z

With the difference of [§4], terms of the second command in

are not neglected any more.

The first relation of balance

(

)

div

xx X

xy y

xz Z

imply the condition then

following on the function of roll:

In addition, without loading external on contour of the section, one must have

N 0

, which

can be written:

y N

Z N

y N

, where

and

are the two components of

normal, or in vectorial form:

(

)

grad N

N CM .x

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

25/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

This determines the function of roll except for a constant. To raise this indetermination,
one writes for example the expression of the normal effort (for a section where torsion produces
roll):

X ds

thus the additional condition on the function of roll is:

In practice, in

MACR_CARA_POUTRE

, one places oneself above all in a reference mark related to the center of torsion

One calculates then

who must check:

(

)

= 0

grad N

N CM .x

The inertia of roll

is obtained then by:

MACR_CARA_POUTRE

fact call to the following elementary controls:

Translation of the co-ordinates of the nodes in the reference mark related to the center of torsion (calculated
previously in table TCARS):

CREA_MAILLAGE (MESH:

IDENTIFY: (TABLE:TCARS NOM_ORIG: “TORSION”));

Assignment of a model (thermal plan), of a material field:

AFFE_MODELE (MESH:

AFFE: (ALL: “YES” PHENOMENON: “THERMAL” MODELING:“PLANE”));

AFFE_MATERIAU (MESH

AFFE: (ALL: “YES” MATER: ));

Boundary conditions on external contour G0:

y N

Z N

y N

F1=DEFI_FONCTION (NOM_PARA: VALE: (0., 0., 10., - 10. )) ;
F2=DEFI_FONCTION (NOM_PARA: VALE: (0., 0., 10., 10. )) ;
CH1 = AFFE_CHAR_THER_F (MODEL:

FLUX_REP: (GROUP_MA: G0 FLUX_X: F1 FLUX_Y: F2)) ;

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

26/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

Condition on the field solution:

: creation of a unit source term on all it

mesh, and of the vector second associate member.

LIAISON_CHAMNO

then allows to impose

desired condition.

CHS = AFFE_CHAR_THER (MODEL:

SOURCE: (ALL: “YES” SOUR: 1.));

VS = CALC_VECT_ELEM (OPTION: “CHAR_THER” CHARGES: CHS…);
MS = CALC_MATR_ELEM (MODEL: … OPTION: “RIGI_THER”);
NUM = NUME_DDL (MATR_RIGI: Ms);
= ASSE_VECTEUR (VECT_ELEM GOES: VS NUME_DDL: NUM);
CH2 = AFFE_CHAR_THER (

LIAISON_CHAMNO: (CHAM_NO: COEF_IMPO GOES: 0.));

Calculation of the function of roll

THER_LINEAIRE (MODEL: ….

EXCIT: (LOAD: CH1)
EXCIT: (LOAD: CH2)

);

Calculation of the constant of roll

and enrichment of the table:

TCARS = POST_ELEM (MODEL:…

CARA_POUTRE: (CARA_GEOM: TCARS

LAPL_PHI:KSI OPTION:“CARA_GAUCHI”));

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

27/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

5 Bibliography

[1]

BATOZ J.L. & DHATT G.: “Modeling of the structures by finite elements. Volume 2, beams
and plates ". HERMES, Paris, 1990

[2]

BLEVINS R.D.: “Formulated for natural frequency and shape mode”. Van Nostrand Reinhold,
New York, 1979.

[3]

COWPER G.R.: “The shear coefficient in Timoshenko' S beam theory”. J. off Applied
Mechanics, June 1966, p 335-340.

[4]

HSU Y.W.: “The shear coefficient off beams off circular cross-country race section”. J. off Applied
Mechanics, March 1975, p 226-228.

[5]

MASSONET C. & CESCOTTO S.: “Mechanical of materials”. Of boeck University,
Brussels, 1994.

[6]

PILKEY W.D.: “Formulated for stress, Strain and Structural Matrices”. Wiley & Sounds, New York,
1994.

[7]

REISSNER E. & TSAI W.T. : “One the determination off the centers off twist and off shear for
cylindrical Shell beams ". J. off Applied Mechanics, december 1972, p 1098-1102.

[8]

BAMBERGER Y.: Run of Resistance of Materials - National School of Bridges and
Roadways. 1994.

[9]

TIMOSHENKO S. Résistance of Materials - Dunod 1968

[10]

Document [U4.24.01]: Operator

AFFE_CARA_ELEM

[11]

VOLDOIRE F: “Elements of resistance of materials. Directed work of the ENPC”. Note
EDF/MN HI-74/96/002/0

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

28/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

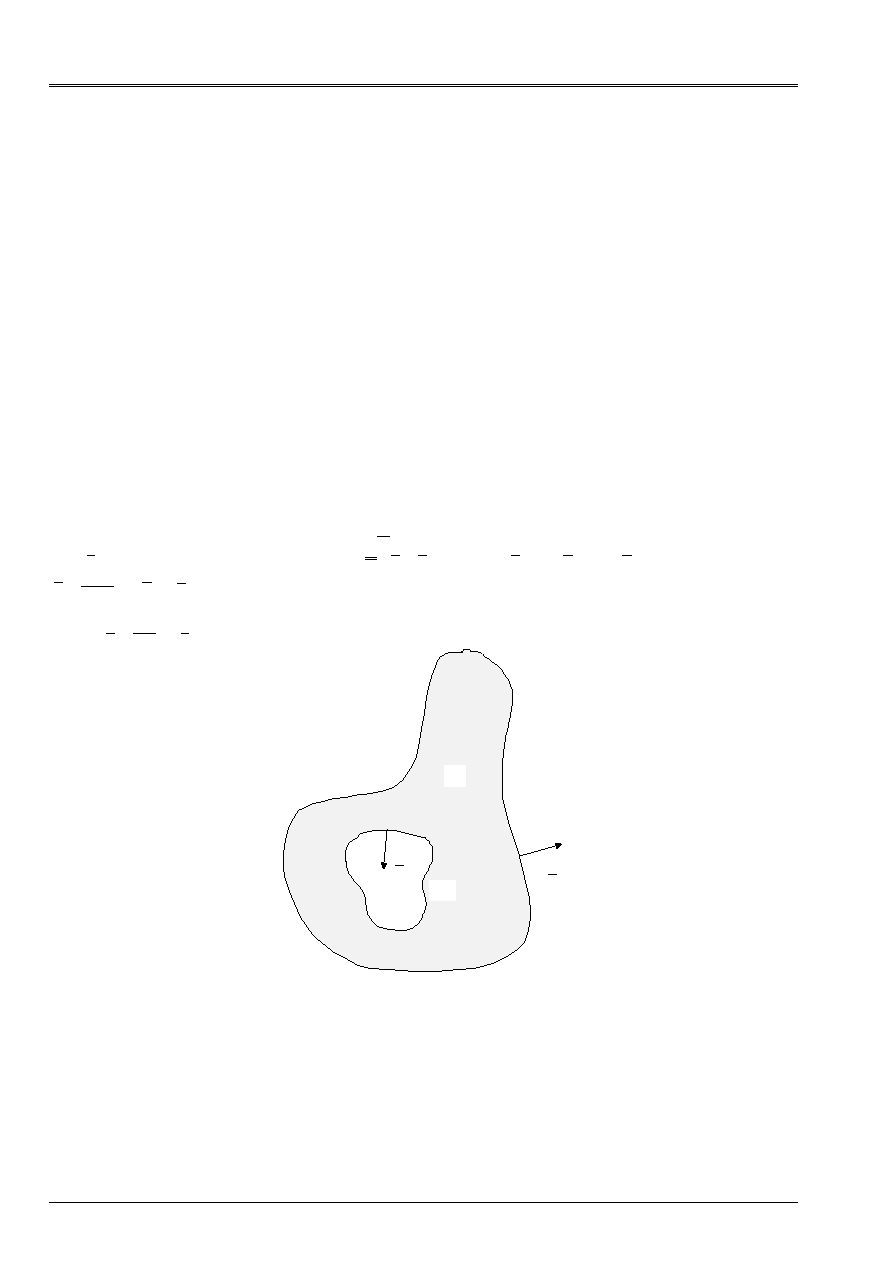
Appendix 1 Determination of the constant of torsion for

sections has borders multiplement related

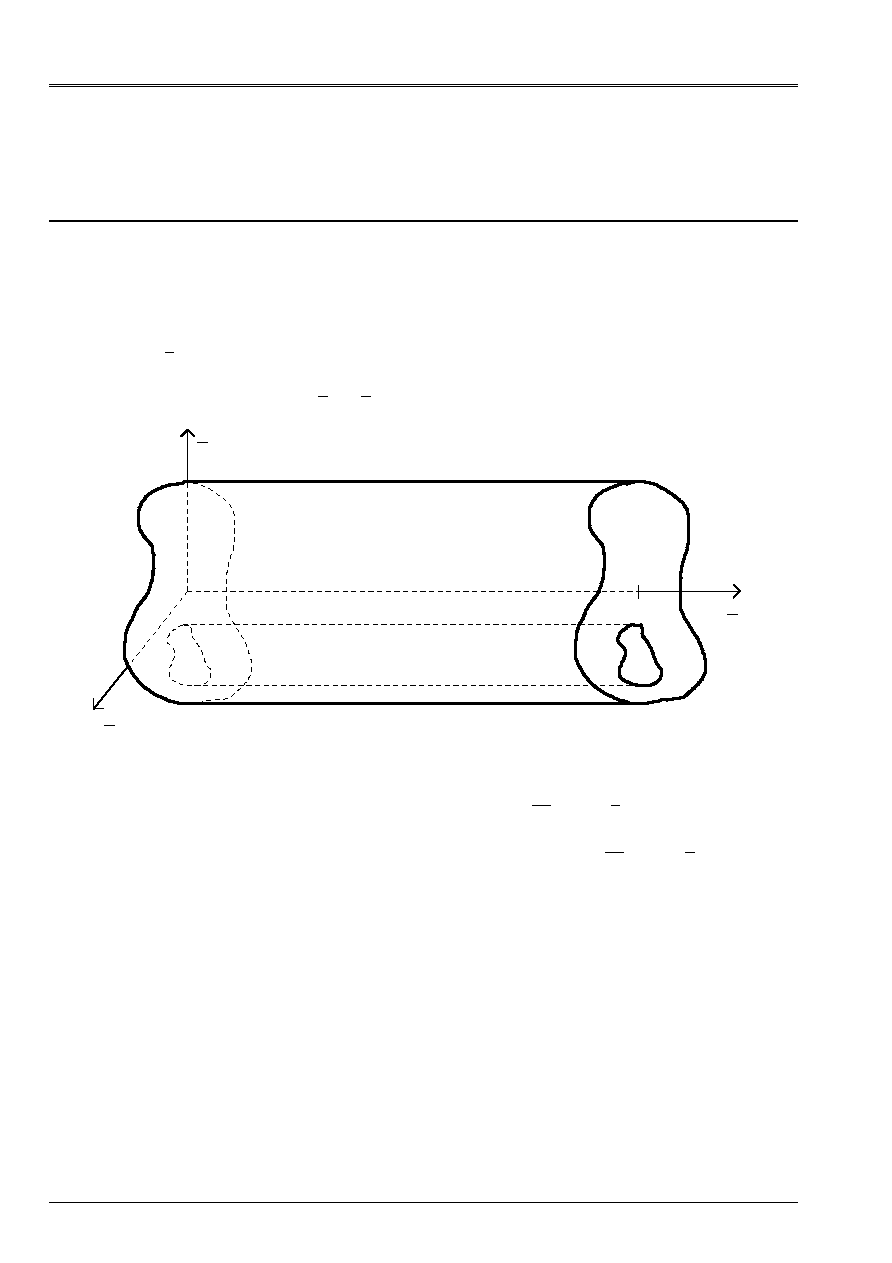
That is to say a beam elastic, isotropic, length

and of unspecified section

who can be not simply

related. One notes

contour external of

and

, for

, possible contours

interiors. One notes

its total border.

The axis is chosen

according to the line of the centers of gravity of the cross-sections. One supposes to simplify

demonstration which the center of torsion is confused with the center of gravity, which makes it possible to uncouple them
effects of torsion and bending. Axes

and

the main directions of inertia are selected following.

Appear A1-a: Beam in unspecified section

The beam is charged on its section

by one torque

M X

In addition, the side surface of the cylinder is not charged and the forces of volume are null.
One immediately deduces from it that the torque from the interior forces at the point

M X

The problem of elasticity posed previously seems incompletely definite. Indeed, conditions
with the limits on the cross-sections

and

are incomplete because there is not a condition in each

not, but on average. There is thus, a priori, an infinity of solutions. The assumption of Saint-Coming consists with
to seek a solution such as the tensor of the stresses is form

The principle of Saint-Coming is valid far from the sections of application of the forces. Indeed, except in cases
particular loadings, the four presumedly null terms diminish exponentially with

To solve this problem of elasticity, a formulation in stresses is chosen. The equations to be written are
thus those of balance and those of compatibility.

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

29/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

Equilibrium equations

div

lead to the three following scalar equations:

1 11

éq A1-1

1 12

1 13

éq A1-2

(with the simplified notation:

)

The equations of Beltrami, which take account of the equations of compatibility are written:

11 11

éq A1-3

- +

éq A1-4

- +

13 11

éq A1-5

éq A1-6

éq A1-7

33 11

éq A1-8

The equations [éq A1-3], [éq A1-6] and [éq A1-8] show that

11 11

and

33 11

are solutions of one

homogeneous linear system and thus that

11 11

33 11

. With the equation [éq A1-7], one deduces some

that

(

) (

)

1 1

X has

has

B X

C X

. By taking account of the fact that one deals with the problem of

free torsion, one will take

no one from now.

The equations [éq A1-2] and [éq A1-5] show that

and

do not depend on

. The equation [éq A1-1]

is written:

()

[

]

()

[

]

F X

G X

where

and

are two arbitrary functions. According to the theorem of Schwartz, there exists

(

)

X X

such as:

()

= -

F X

G X

F X

G X

The equations [éq A1-4] and [éq A1-5] give:

0
0

=
=

that is to say

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

30/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

where

is a constant of integration. Like

and

are arbitrary, one will take them identically null.

The problem to be solved is thus a problem of Laplacian:

then

It remains to write the boundary conditions, who will allow us to write conditions on

for

and on

The boundary conditions are to be written on all the border.

On the cross-sections

(and the same in

), one a:

2 13

3 12

éq A1-9

That is to say

the normal external with

. One has

N 0

. One poses

. One can also write

grad

;

the tangential part of the stress in the cross-section is called. That is to say

the point

running of contour

for

. The condition, on side surface, stated higher, can

to be written

Appear A1-b: Definition of the normals

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

31/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

Thus, on the side surface of a beam, the vector forced tangential

is tangent with contour.

The equation

conduit in a condition which must observe

on contour:

The equation [éq A1-9] led to

2 2

3 3

that one can also write:

X dx

(

)

The problem to solve to obtain

is thus:

with the stress

(

)

X dx

It remains to identify the constant of torsion C.

The law of behavior of the beams in torsion is:

(cf [§3]).

To solve the preceding problem more easily, one poses

and

= -

, the problem with

to solve becomes then:

= -

(

)

X dx

= -

With such a notation, one obtains

(

)

X dx

Contour

consists of several contours: an external contour

and

interior contours

. The condition

conduit with

following conditions:

for

are constant unknown factors. By noting that

, and thus

, is defined except for a constant, one can fix one

. One will thus take

. Remain to determine

for

For that, one will study the roll of the cross-section of X-coordinate

. Let us recall that the tensor of

stresses is written (cf [§4]):

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

32/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

One poses

grad

;

is (except for a constant) the tangential part of the vector forced in

cross-section.

One thus has:

grad

= -

GM X

One makes circulate this equation along

, one a:

DLL

X dx

One was useful oneself here owing to the fact that the circulation of the gradient on a closed curve is null.

It is noted that the first integral can be written in term of flow of

beam

. In addition, the second

integral is equal to

()

Finally, the problem is written:

= -

()

N DLL

Once solved this problem, one a:

()

The last condition:

()

N DLL

is difficult to treat in a numerical way. Actually, both

conditions on each border bordering a hole are written:

()

Variational formulation:

()

v H

such as

()

v D

v DLL

v D

v DLL

DLL

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

33/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

The function is considered

such as

. Matriciellement, one a:

[]

[] []

Where

[]

is the vector whose components are related to form.

Under these conditions, the variational approximation of the weak formulation gives:

[]

[] []

[]

Where one posed:

[]

F v

v D

[] []

()

T v

v DLL

[]

One can check that the condition on flow is checked:

[]

[] [] [] []

[]

()

N DLL

DLL

= -

444

1 2

4 3

It is seen, with this new formulation, that the posed mathematical problem returns to a problem of
linear thermics with a particular loading. This is easily programmable in Code_Aster.

By applying the preceding method to a beam whose cross-section is the crown ranging between
radii

and

with

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

34/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

There is the following problem to solve:

= -

(

)

(

)

N DLL

The general solution of the problem is written

()

= -

With

Here, one has

R E

= -

. From where

()

With

. In addition, one

()

. Finally:

()

= -

One can now calculate

()

. One has

= -

and

()

. All

made calculations, there is the conventional result:

(

)

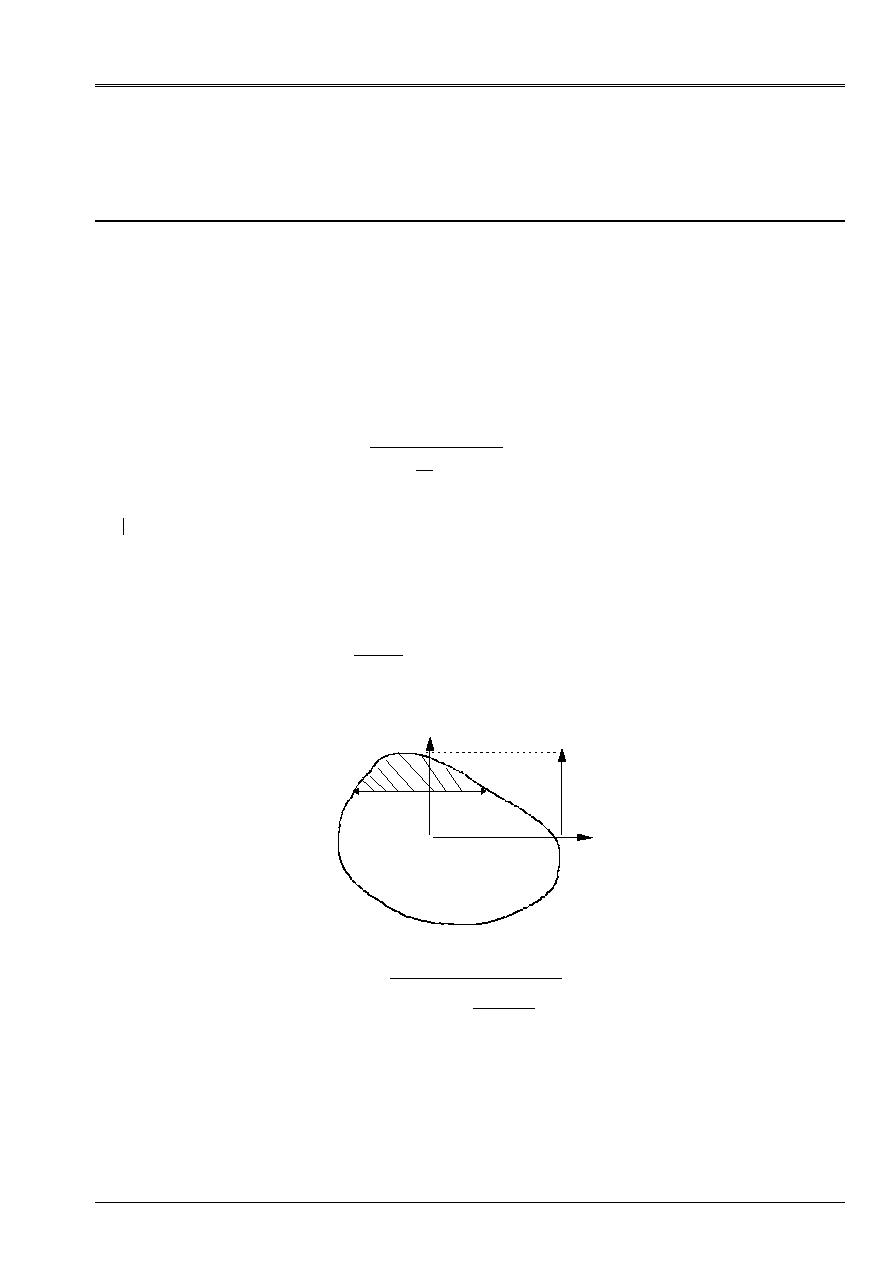
Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

35/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

Appendix 2 Determination of the constant of shearing of one
beam equivalent to a whole of parallel beams

A2.1 Position of the problem:

One clarifies here a method developed in the control

MACR_CARA_POUTRE

to obtain the coefficients

of shearing AY and AZ of a beam equivalent to a whole of disjoined beams (e.g. embedded posts
between two floors). This makes it possible for example to carry out models “skewers” of ships, it is with
to say condensed in only one beam.

For only one beam, the definition of the coefficients of shearing rests on the energy method [§2.1.3]:
the formulation is based on complementary energy due to shearing in the section.

The coefficient of shearing is:

[

]

G G

Note:

This expression is still valid in the case of a heterogeneous beam (G variable).

The distribution of shear stress in the section, for only one beam, is based on the formula of
Jourawski, [§2.1.1] which provides the distribution of shear stresses due to a shearing action in one
direction and only the average of shearings in the other direction.
The formula of Jourawski is written:

m y

I B y V

()

with

()

m y

T B T dt

()

max

Quantity

()

m y

represent the static moment on behalf of section A included/understood enters

and

max

B (y)

max

With

Then K can be written in the form:

y Dy

()

max

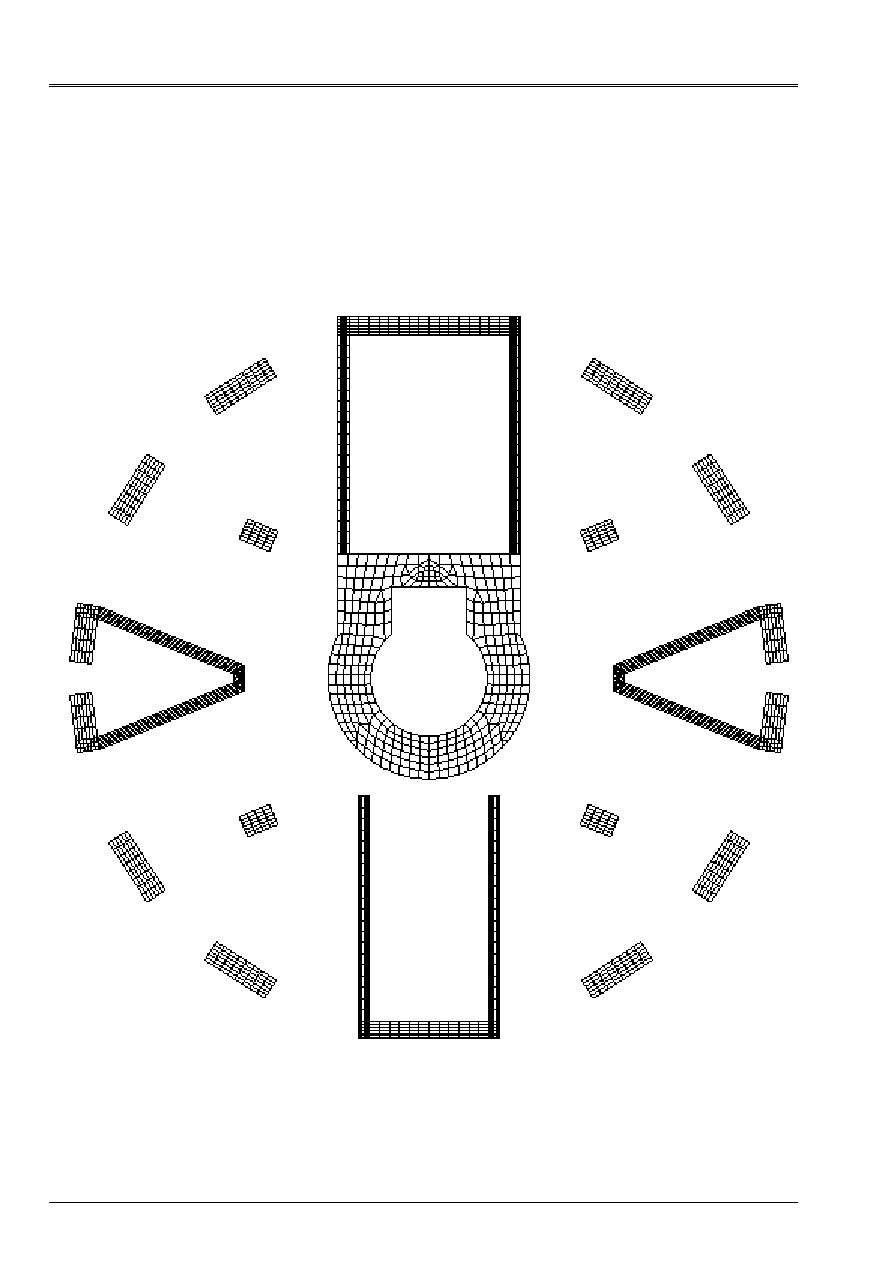
Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

36/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

The subjacent idea is that the section supports normal stresses resulting from the theory of the beams
of Euler, and whom one evaluates the effort of slip of A on B.

For a nonrelated section, like the section out of cut of a ship, the assumption of Jourawski cannot
to be made (except considering that all the section becomes deformed axially like the same beam with each
X-coordinate X). One cannot know a priori the distribution of shearings nor of the normal stresses in
each post. The following figure gives an idea of the cross-section of a ship jet engine:

Appear A2.1-a: Section of a ship jet engine

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

37/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

A2.2 Expression simplified of the coefficients of shearing

Assumption: the posts are embedded in the floors: the ship seen on side can be represented
like a whole of parallel posts embedded between two floors:

Appear A2.2-a: together of posts between two boards

This particular case is calculated: each post is a rectangular beam of section (the main axes
of inertia of the various posts are not colinéaires). H=3 with 4m.

The beams are embedded at the two ends. It is then necessary to seek a relation between an effort F imposed on
higher floor, and the displacement of this floor in the same direction, i.e. to calculate the rigidity of
this system in this direction.

A2.2.1 For a beam:

The method used is exposed for example in [bib11].

Beam fixed at an end and free with the other:

The system is isostatic and elastic. One wants to express displacement U (H) according to F and

Principle of Virtual Work is written:

U, X

v, y

F H v H

v DLL

M v

E I

V v
G S

(). ()

. ()

()

()
.

()

()
.

for any virtual displacement v, and a specific effort F in y=H, (here the normal effort is null).

F=1 is chosen, and one calculates successively displacements due to an effort F and a couple

in y=H. In

integrating the preceding expression, it is found that, under the effect F, displacement U real and rotation are worth:

U H

F H

E I

F H

G S

F H

E I

I.E.(internal excitation)

G H S

()

with

K S

and

()

F H

E I

= -

Under the effect of the moment

, one obtains:

U H

E I

()

= -

()

E I

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

38/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

If the beam has a rectangular section of width B and thickness H, one obtains:

bhk

5
6

for F imposed:

U H

F H

E bh

()

(

)

4 12

()

F H

E bh

= -

for

imposed:

U H

E bh

()

= -

()

E bh

Beam fixed at the two ends: (embedding slipping in y=H)

The system is hyperstatic degree 1.

One expresses displacement U (H) according to the hyperstatic unknown factors
F and

using the preceding results.

Under the effect F and

, displacement U real and rotation (null because of embedding) are worth:

U H

F H

E I

F H

E I

F H

E bh

()

(

)

4 12

= -

F H

I.E.(internal excitation)

E I

F H

E bh

The resolution of this system makes it possible to obtain U (H) according to F:

U H

F H

I.E.(internal excitation)

GH S

F H

E bh

I.E.(internal excitation)

GH S

U H

E bh

U H

K U H

()

(

)

()

(

)

()

. ()

1 12

One also finds this result by considering the matrix of rigidity of an “exact” element of beam with 2
nodes ([bib1] or [R3.08.01]). The term above corresponds exactly at the end of rigidity of sharp effort
only according to direction X:

(

)

I.E.(internal excitation)

GH S

I.E.(internal excitation)

GH kS

Note:

The embed-free situation differs only from one coefficient (4 instead of 1):

U H

F H

E bh

()

(

)

4 12

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

39/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

The two possibilities are offered in

MACR_CARA_POUTRE

the two ends are embedded (actually one is embedded, the other is embedded in a floor
mobile: slipping embedding)

the higher end is free (makes some in connection rotulée with the higher floor).

One can thus propose to express rigidity with the shearing action of each post in the form:

I.E.(internal excitation)

GH S

U H

()

. ()

with

embedded embedded

embedded free

A2.2.2 For a whole of beams

The method consists in calculating the rigidity of each post in the preceding way, and to compare rigidity
of the whole to that of an equivalent beam embedded between two floors. For that one expresses the effort
total edge applied to the whole of the posts (for example in the direction y):

K U

Each post having an unspecified orientation compared to the total axes, it is necessary for all to express them
efforts

in the total reference mark:

x1 and x2 indicating the main axes of inertia of
post I, sharp effort

in this reference mark is:

= -

cos ()

sin ()

cos ()

Moreover, one supposes that total displacement U of the whole of the posts is uniform (components

and

) and must be colinéaire with the shearing action T. (what is not certain: couplings are possible if it

does not have there particular symmetries). This involves for the direction y:

cos ()

sin ()

and

K U

=
=

one obtains:

(

)

(

)

K U

y y

cos ()

sin ()

cos ()

sin ()

with

I.E.(internal excitation)

GH S

in the same way in direction Z:

= -

sin ()

cos ()

thus

(

)

K U

Z Z

sin ()

cos ()

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

40/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

In addition, for the equivalent beam, one makes the assumption that rigidity with the shearing action S `expresses
even way that that of each beam:

(

)

K U

I.E.(internal excitation)

S H Gk

eq y

zeq

yeq

with

In fact, it would have to be checked that energies due to the bending and the normal effort are quite negligible.

The two expressions of the shearing action lead to the expression of the coefficient of equivalent shearing:

I.E.(internal excitation)

GS H

I.E.(internal excitation)

H K

and in direction Z:

I.E.(internal excitation)

GS H

I.E.(internal excitation)

H K

A2.3 Method used in

MACR_CARA_POUTRE

By using the assumptions described previously, namely:

only rigidity due to the shearing action is taken into account in the calculation of the coefficients of shearing

the equivalent beam is embedded on the two floors

two design assumptions are to be envisaged concerning each post (embed-ball joint and embedded
embedded).

one can propose a method of calculation in

MACR_CARA_POUTRE

to obtain coefficients of

shearing are equivalent to a whole of beams of parallel axes, embedded in a floor with one of
their ends, and free with the other, or embedded at the other end.

Restrictions of use:

it is reasonable to place the equivalent beam on the center of gravity of the whole of the posts, and in
the main reference mark of inertia of the unit, to avoid the parasitic couplings

it is necessary to ensure the continuity of all the DDL of the equivalent beam (translation and rotation) with the DDL
floors (what modelizes the embedding of the beam in the floor), which forces to modelize it
floor in elements of hulls or, if it is with a grid in 3D, to connect it using beams or of plates.

A2.3.1 the method of calculation is as follows:

1) For each post, to make usual calculation by

MACR_CARA_POUTRE

geometrical characteristics and

coefficients of shearing of the section, in the main reference mark of inertia of each section (already
available)

2) Always for each section, calculation of rigidity to shearing (the user must provide H, distance enters

floors):

(

)

(

)

I.E.(internal excitation)

S H Gk

I.E.(internal excitation)

S H Gk

with

Code_Aster

Version

7.4

Titrate:

Calculation of the characteristics of a beam of cross section unspecified

Date:

01/09/05

Author (S):

J.M. PROIX, NR. LAURENT, P. HEMON, G. BERTRAND

Key:

R3.08.03-C

Page

41/42

Manual of Reference

R3.08 booklet: Machine elements with average fiber

HT-66/05/002/A

3) Calculation of rigidity equivalent to the whole of the beams:

(

)

cos ()

sin ()

(

)

sin ()

cos ()

4) Calculation of the coefficients of shearing are equivalent:

I.E.(internal excitation)

GS H

I.E.(internal excitation)

H K

I.E.(internal excitation)

GS H

I.E.(internal excitation)

H K

knowing that

and

are already calculated by

MACR_CARA_POUTRE

For the key words of the control

MACR_CARA_POUTRE

, one needs that the user provides H, by the key word

LENGTH

, characteristics (constant) of the material (key word

MATERIAL

) and chooses the conditions with

limits by the key word

CONNECTION

CONNECTION: BALL JOINT

CONNECTION: EMBEDDING

This calculation is of course activated only if several

GROUP_MA

are defined by the user (indicating that the section

is made up of under disjoined parts).