
Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
1/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
Organization (S):
EDF-R & D/AMA
Instruction manual
U4.4- booklet: Modeling
Document: U4.43.01
Operator
DEFI_MATERIAU
1 Goal
To define the behavior of a material or the parameters associated with fatigue, the damage, or with
simplified methods.
The allowed laws of behavior currently by this operator relate to the following fields:
Linear mechanics and Thermics or not, Metallurgical for the modeling of steels,
Hydration and Drying for the concretes, Fluid for accoustics, Thermo Hydro-mechanical for
the modeling of the porous environments saturated with thermomechanical coupled and Soil mechanics.
If necessary, the same material can be defined at the time of a call to DEFI_MATERIAU with several
behaviors, such as rubber band, thermics,…
Product a Structure of data of the type MATER.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
2/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
Count
matters

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
3/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
4.9
Key words factors
ECOU_VISC1
,
ECOU_VISC2
,
ECOU_VISC3
,
ECRO_CIN1
,
ECRO_CIN2
,

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
4/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
6.4.2
Operands COND_LMM/COND_LMP/COND_LPP/COND_LSI/COND_TMM/

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
5/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
6/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
7/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
8/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
9/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
10/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
11/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
12/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
13/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
14/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
2 Syntax
general
my [to subdue] = DEFI_MATERIAU
(
# Behavior General Rubber bands [§ 3]
|
/
ELAS,
#
to see [§
3.1]
/
ELAS_FO,
/
ELAS_FLUI, #
to see [§
3.2]
|
APPUI_ELAS,
#
to see [§
3.3]
|
CABLE,
#
to see [§
3.4]
|
/
ELAS_ORTH, #
to see [§
3.5]
/
ELAS_ORTH_FO,
|
/
ELAS_ISTR, #
to see [§
3.6]
/
ELAS_ISTR_FO,
|
/
ELAS_COQUE,
#
to see [§
3.7]
/
ELAS_COQUE_FO,
# General Nonlinear Mechanical Behaviors [§ 4]
|
TRACTION,
#
to see [§
4.1]
|
/
ECRO_LINE, #
to see [§
4.2]
/
ECRO_LINE_FO,
|
/
PRAGER, #
to see [§
4.3]
/
PRAGER_FO,
|
CHABOCHE,
#
to see [§
4.4]
|
/
CIN1_CHAB, #
to see [§
4.5]
/
CIN1_CHAB_FO,
|
/
CIN2_CHAB, #
to see [§
4.6]
/
CIN2_CHAB_FO,
|
/
TAHERI, #
to see [§
4.7]
/
TAHERI_FO,
|
/
POLY_CFC,
#
to see [§
4.8]
/
POLY_CFC_FO,
| ECOU_VISC1,
# to see [§
4.9]
| ECOU_VISC2,
| ECOU_VISC3,
| ECRO_CIN1,
| ECRO_CIN2,
| ECRO_ISOT1,
| ECRO_ISOT2,
|
/
LEMAITRE,
#
to see [§
4.10]
/
LEMAITRE_FO,
|
VISC_SINH,
# to see [§
4.11]
|
/
LEMA_SEUIL,
#
to see [§
4.12]
/
LEMA_SEUIL_FO,

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
15/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
|
ZIRC_CYRA2,
#
to see [§
4.13]
|
ZIRC_EPRI, #
to see [§
4.14]
|
VISC_IRRA_LOG,
#
to see [§
4.15]
|
/
LMARC,
#
to see [§
4.16]
/
LMARC_FO,
# Behaviors related to the damage and the rupture [§ 5]
|
/
ROUSSELIER,
#
to see [§
5.1]
/
ROUSSELIER_FO,
|
/
VENDO_CHAB,
#
to see [§
5.2]
/
VENDO_CHAB_FO,
|
ENDO_ORTH_BETON,
#
to see [§
5.3]
|
NON_LOCAL, #
to see [§
5.4]
|
/
RUPT_FRAG, #
to see [§
5.5]
/
RUPT_FRAG_FO,
|
CORR_ACIER,
#
to see [§
5.6]
#
Behaviors
Thermics
[§
6]
|
/
THER,
#
to see [§
6.1]
/
THER_FO,
/
THER_ORTH, #
to see [§
6.2]
/
THER_NL,
#
to see [§
6.3]
/
THER_COQU, #
to see [§
6.4]
/
THER_COQU_FO,
# Behaviors specific to the concretes [§ 7]
|
THER_HYDR, #
to see [§
7.1]
|
SECH_GRANGER,
#
to see [§
7.2]
|
SECH_MENSI,
#
to see [§
7.3]
|
SECH_BAZANT,
#
to see [§
7.4]
|
SECH_NAPPE,
#
to see [§
7.5]
|
PINTO_MENEGOTTO,
#
to see [§
7.6]
|
BPEL_BETON
and
BPEL_ACIER,
#
to see [§
7.7]
|
BETON_DOUBLE_BP,
#
to see [§
7.8]
|
GRANGER_FP, GRANGER_FP_INDT and V_GRANGER_FP,
#
to see [§
7.9]
|
NADAI_B,
#
to see [§
7.10]
|
BAZANT_FD, #
to see [§
7.11]
|
LABORD_1D, #
to see [§
7.12]
|
/
MAZARS, #
to see [§
7.13]
/
MAZARS_FO,
|
BETON_UMLV_FP,
#
to see [§
7.14]
|
BETON_ECRO_LINE,
#
to see [§
7.15]
|
GLRC,
#
to see [§
7.16]
|
JOINT_BA,
#
to see [§
7.17]
#
Behaviors
Metal-worker-mechanics
[§
8]
|
META_ACIER,
#
to see [§
8.1]
META_ZIRC, #
to see [§
8.2]
|
DURT_META, #
to see [§
8.3]
|
/
ELAS_META, #
to see [§
8.4]
/
ELAS_META_FO,
|
META_ECRO_LINE,
#
to see [§
8.5]
|
META_TRACTION,
#
to see [§
8.6]
|
META_VISC, #
to see [§
8.7]
|
META_PT,
#
to see [§
8.8]
|
META_RE,
#
to see [§
8.9]

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
16/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
# Thermo Behaviors Hydro-mechanical and of the grounds [§ 9]
COMP_THM =/`LIQU_SATU `, # to see [§ 9.1]
/`LIQU_GAZ `,
/`GAS `,
/`LIQU_GAZ_ATM `,
/`LIQU_VAPE_GAZ `,
/`LIQU_VAPE `,
/`LIQU_SATU_GAT `,
/`LIQU_NSAT_GAT `,
/`LIQU_AD_GAZ_VAPE `,
|
THM_INIT,
#
to see [§
9.2]
|
THM_LIQU,
#
to see [§
9.3]
|
THM_GAZ,
#
to see [§
9.4]
|
THM_VAPE_GAZ,
#
to see [§
9.5]
|
THM_AIR_DISS,
#
to see [§
9.6]
|
THM_DIFFU, #
to see [§
9.7]
|
SURF_ETAT_SATU,
#
to see [§
9.8]
|
SURF_ETAT_NSAT,
#
to see [§
9.9]
|
CAM_CLAY_THM,
#
to see [§
9.10]
|
CAM_CLAY,
#
to see [§
9.11]
|
CJS, #
to see [§
9.12]
|
LAIGLE, #
to see [§
9.13]
|
DRUCKER_PRAGER,
#
to see [§
9.14]
|
BARCELONA, #
to see [§
9.15]
|
HOEK_BROWN,
#
to see [§
9.16]
# Behavior specific to the elements 1D [§ 10]
|
/
VMIS_POUTRE,
#
to see [§
10.1]
/
VMIS_POUTRE_FO,
|
ECRO_FLEJOU,
#
to see [§
10.2]
|
ECRO_ASYM_LINE,
#
to see [§
10.3]
#
Behaviors
private individuals
[§
11]
|
LEMAITRE_IRRA,
#
to see [§
11.1]
|
LMARC_IRRA,
#
to see [§
11.2]
|
DIS_GRICRA,
#
to see [§
11.3]
|
GATT_MONERIE,
#
to see [§
11.4]
|
DIS_CONTACT,
#
to see [§
11.5]
|
ASSE_CORN, #
to see [§
11.6]
|
ARM,
#
to see [§
11.7]
#
Behavior
fluid
[§
12]
|
FLUID, #
to see [§
12.1]
# Given Materials associated with postprocessings [§ 13]
|
TIRE,
#
to see [§
13.1]
|
DOMMA_LEMAITRE,
#
to see [§
13.2]
|
CISA_PLAN_CRIT,
#
to see [§
13.3]
|
/
WEIBULL,
#
to see [§
13.4]
/
WEIBULL_FO,
|
/
RCCM,
#
to see [§
13.5]
/RCCM_FO,
)
Notice
:
For the majority of the behaviors, it is possible to define constant characteristics or
many characteristics depending on one or two variables. We chose to gather them
two key words factors, single-ended spanner words being identical in both cases, only them
arguments are characterized by the type of associated concept.
In the syntax of each behavior, one will adopt following convention to indicate it or
the variables of which can depend the concepts of the type
function
.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
17/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
[function *]
“TEMP” “X”, “Y”, “Z”
(two variables among four),
[function **]
“TEMP”
[function ***]
“EPSI” “TEMP”
[function ****] “ABSC”
[function +]
“INST”
[function ++]
'
NORM
'

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
18/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
3
General elastic behaviors
3.1
Key words factor
ELAS/ELAS_FO
Definition of the constant linear elastic characteristics or functions of the parameter
“TEMP”
.
3.1.1 Syntax
|
/
ELAS
=
_F
(
E
=
yg
,
[R]
NAKED =
naked, [R]
RHO =
rho, [R]
ALPHA
= dil
, [R]
/AMOR_ALPHA
=
, [R]
AMOR_BETA
=
,
[R]
/
AMOR_HYST
=
,
[R]
)
/
ELAS_FO
=
_F
(
E
=
yg
,
[function **]
NAKED
= naked
,
[function **]
RHO
=
rho
, [R]
ALPHA
= dil
, [function **]
/AMOR_ALPHA
=
,
[function **]
AMOR_BETA
=
,
[function **]
/
AMOR_HYST
=
,
[function **]
TEMP_DEF_ALPHA=
Tdef,
[R]
PRECISION
=/
, [R]
/
1
,
[DEFECT]
K_DESSIC =/
K
, [R]
/
O
,
[DEFECT]
B_ENDOGE =/
E
, [R]
/
O
,
[DEFECT]
FONC_DESORP
=
/
F
, [function]
)
3.1.2 Operands
E/NAKED
E = yg
Young modulus. It is checked that E 0.
NAKED = naked
Poisson's ratio. It is checked that
- 1.
naked
0.5
.
3.1.3 Operand
RHO
RHO = rho
Real constant density (one does not accept a concept of the type
function
). Not
checking of about size.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
19/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
3.1.4 Operands
ALPHA/TEMP_DEF_ALPHA/PRECISION
ALPHA =
[function **]
Isotropic thermal expansion factor.
The thermal expansion factor is an average expansion factor which can depend on
the temperature
T
.
The values of the expansion factors are determined by tests of dilatometry which have
place at the ambient temperature (0°C or more generally 20°C).
So one in general has the values of the expansion factor defined compared to 20°C
(temperature to which one supposes the null thermal deformation).
Certain studies require to take a temperature of reference different from
ambient temperature (null thermal deformation for another temperature that
ambient temperature). It is then necessary to carry out a change of reference mark in the calculation of
thermal deformation [R4.08.01].
TEMP_DEF_ALPHA = Tdef
[R]
It is the value of the temperature to which the values of the thermal expansion factor have
summer determined, and were well informed under the key word
ALPHA
.
This key word becomes obligatory as soon as ALPHA was informed.
The calculation of the thermal deformation is done by the formula [R4.08.01]:
()
()
(
)
()
()
(
) () (
)
()
HT
ref.
def
ref.
ref.
def
ref.
HT
ref.
T
T T T
T
T T T
T
T
T
T T
T
=
-
=
-
-
-
-
=
$
$
with
and
0
PRECISION: /prec
/
1.
[DEFECT]
This key word is used when the key word
TEMP_DEF_ALPHA
is specified.
It is a reality which indicates with which precision a temperature
T
I
(of the list of the temperatures
being used for the definition of
()
T
I
I
NR
,
,
=1
) is close to the temperature of reference
T
ref.
.
This reality is used for calculation of the function
()
$
T
I
. The mathematical formula allowing the calculation of
()
$
T
I
is different according to whether
T
T
T
T
I
ref.
I
ref.
=
or
.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
20/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
3.1.5 Operands
AMOR_ALPHA
/
AMOR_BETHA
/
AMOR_HYST
/AMOR_ALPHA
=
AMOR_BETA
=
Coefficients
and allowing to build a matrix of viscous damping
proportional to rigidity and/or the mass [C] =
[K] + [M]. One will refer to the documents
of modeling of the mechanical cushioning [U2.06.03] and [R5.05.04].
/AMOR_HYST =
Coefficient
of damping hysteretic allowing to define the complex Young modulus
(viscoelastic material) from which the matrix of complex rigidity will be created
allowing the calculation of the harmonic answer [U2.06.03] and [R5.05.04].
3.1.6 Operands
K_DESSIC
/
B_ENDOGE
/K_DESSIC = K
Coefficient of withdrawal of dessication.
/K_ENDOGE = E
Coefficient of withdrawal of endogenous.
These characteristics are used with the behavior defined by key words BETON_DOUBLE_BP,
GRANGER_FP and BAZANT_FD.
3.1.7 Operand
FONC_DESORP
FONC_DESORP: curve of sorption-desorption [R7.01.12] giving the hygroscopy H according to
water content C. Operand obligatory with law BAZANT_FD [R7.01.01].
3.2
Key word factor
ELAS_FLUI
The key word
ELAS_FLUI
allows to define the equivalent density of a tubular structure
with internal and external fluid, by taking of account the effect of containment.
This operation lies within the scope of the study of the dynamic behavior of a configuration of
type “beam of tubes under transverse flow”. The study of the behavior of the beam is
brought back to the study of a single tube representative of the whole of the beam.
Equivalent density of the structure
eq
is defined by:
(
)
(
)
[
]
eq
E
I
I
I
T
E
I
E
eq
eq
E
I
E
T
E
I
D
D
D
D
D
D
D
Cm D
D D
Cm
=
-
+
-
+
=
1
2
2
2
2
2
2
2
2
2
.
.
.
.
.
,
,
,
are respectively the density of the fluid
intern, of the external fluid and the structure.
are respectively the external diameter and intern of the tube.
is a coefficient of added mass (containment defines).

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
21/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
3.2.1 Syntax
/ELAS_FLUI = _F
(
RHO
=
rho
[R]
E
=
yg
[R]
NAKED
=
naked
[R]
PROF_RHO_F_INT
=
rhoi [function ****]
PROF_RHO_F_EXT
=
rhoe [function ****]
COEF_MASS_AJOU
=
fonc_cm [function ****]
)
3.2.2 Operand
ELAS_FLUI
/
ELAS_FLUI = _F
(
Key word factor allowing to calculate the equivalent density of a structure beam
with internal and fluid fluid external (this relation of behavior cannot be used
that with elements of beam).
RHO = rho
Density of material.
E = yg
Young modulus.
NAKED = naked
Poisson's ratio.
PROF_RHO_F_INT = rhoi
Concept of the type [
function
] defining the profile of density of the fluid it interns
length of the tube. This function is parameterized by the curvilinear X-coordinate.
PROF_RHO_F_EXT = rhoe
Concept of the type [
function
] defining the profile of density of the external fluid
along the tube. This function is parameterized by the curvilinear X-coordinate,
“ABSC”
.
COEF_MASS_AJOU = fonc_cm
Concept of the type [
function
] produced by the operator
FONC_FLUI_STRU
[U4.35.02].
This constant function, parameterized by the curvilinear X-coordinate, provides the value of
coefficient of added mass
Cm
.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
22/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
3.3
Key word factor
APPUI_ELAS
/APPUI_ELAS = _F (
E_N =
rign,
[R]
E_TAN
=
/
0. ,
[DEFECT]
/
rigt
,
[R]
)
This key word factor makes it possible to define the characteristics of material associated with modeling
“APPUI_REP”
[U4.41.01]. This modeling relates to only the elements of the face type of
modeling
“3D”
associated the phenomenon
“MECHANICAL”
.
One modelizes the action of a medium characterized by the normal and tangential surface stiffness on
faces of three-dimensional elements.
In the case of the elements of hull, it is necessary to duplicate the meshs thanks to the control
CREA_MAILLAGE
[U4.23.02] and to affect modeling
“3D”
with these new meshs.
E_N
=
rign,
[R]
Value of the normal surface stiffness.
E_TAN = rigt,
[R]
Value of the tangential surface stiffness.
3.4
Key word factor
CABLE
Definition of the elastic characteristic nonlinear, constant, for the cables: two behaviors
different rubber bands in traction and compression, defined by the Young moduli
E
and
EC.
(module
in compression).
The standard characteristics of elastic material are to be informed under the key word factor ELAS.
3.4.1 Syntax
/
CABLE
=
_F (
EC_SUR_E =/ecse,
[R]
/
1.D-4,
[DEFECT]
)
3.4.2 Operands
of elasticity
EC_SUR_E = ecse
Report/ratio of the modules to compression and traction. If the module of compression is null, it
total linear system with displacements can become singular. It is the case when a node
is connected only to cables and that those all enter in compression.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
23/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
3.4.3 Operand of mass
RHO = rho
Density.
3.4.4 Operand of dilation
ALPHA = dil
Thermal expansion factor average compared to the temperature of reference defined under
AFFE_MATERIAU.
3.4.5 Operands
of damping
AMOR_ALPHA =
AMOR_BETA =
Coefficients
and allowing to build a matrix of viscous damping proportional to
rigidity and/or with the mass [C] =
[K] + [M]. One will refer to the document modeling of
mechanical cushioning [U2.06.03].

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
24/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
3.5
Key words factor
ELAS_ORTH
/
ELAS_ORTH_FO
Definition of the constant orthotropic elastic characteristics or functions of the temperature for
elements of hull and solid elements isoparametric or layers constitutive of one
composite (cf DEFI_COQU_MULT).
3.5.1 Syntax
/
ELAS_ORTH
=
_F
(
E_L =
ygl, [R]
E_T =
ygt, [R]
E_N =
ygn, [R]
G_LT =
glt, [R]
G_TN =
gtn, [R]
G_LN =
gln, [R]
NU_LT =
nult,
[R]
NU_TN =
nutn,
[R]
NU_LN =
nuln,
[R]
ALPHA_L =
/dil,
[R]
/
0.0,
[DEFECT]
ALPHA_T =
/known as,
[R]
/
0.0,
[DEFECT]
ALPHA_N =
/DIN,
[R]
/
0.0,
[DEFECT]
RHO =
/rho,
[R]
/
0.0,
[DEFECT]
XT =
/trl,
[R]
/
1.0,
[DEFECT]
TESTSTEMXÇ =
/neck,
[R]
/
1.0,
[DEFECT]
YT =
/trt,
[R]
/
1.0,
[DEFECT]
TESTSTEMYÇ =
/cot,
[R]
/
1.0,
[DEFECT]
S_LT =
/cis,
[R]
/
1.0,
[DEFECT]
)
/
ELAS_ORTH_FO
=_F
(
E_L =
ygl, [function **]
E_T =
ygt, [function **]
E_N =
ygn, [function **]
G_LT =
glt, [function **]
G_TN =
gtn, [function **]
G_LN =
gln, [function **]
NU_LT =
nult,
[function **]
NU_TN =
nutn,
[function **]
NU_LN =
nuln,
[function **]
ALPHA_L
=
dil
, [function **]
ALPHA_T
=
known as
, [function **]
ALPHA_N
=
DIN
, [function **]
RHO =
/rho,
[R]
/
0.0,
[DEFECT]
TEMP_DEF_ALPHA = Tdef, [R]
PRECISION
=/
,
[R]
/
1.,
[DEFECT]
)
Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
25/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
3.5.2 Operands
of elasticity
The reader will be able to refer to following documentations:
[U4.42.03]
DEFI_COQU_MULT
[U4.42.01]
AFFE_CARA_ELEM
to define the reference mark of orthotropism (L, T, NR) related to the elements.
E_L = ygl
Longitudinal Young modulus.
NR
T
L
L, T and NR: directions of orthotropism
longitudinal, transverse and normal
E_T = ygt
Transverse Young modulus.
E_N = ygn
Normal Young modulus.
GL_T = glt
Modulus of rigidity in plan LT.
G_TN = gtn
Modulus of rigidity in plan TN.
G_LN = gln
Modulus of rigidity in plan LN.
Note:
For the hulls, the transverse moduli of rigidity are not obligatory; in it
case, one calculates in thin hull by assigning an infinite rigidity to transverse shearing
(DST elements, DSQ and Q4G).
NU_LT = nult
Poisson's ratio in plan LT.
Important remarks:
nult
is not equal to
nutl
. In fact, one with the relation:
nult
ygl
ygt
nutl
*
=
nult
must be interpreted in the following way:
if one exerts a traction according to the axis
L
giving place to a deformation according to this axis equalizes with
ygl
L
L
=
, there is a deformation according to the axis
T
equalize with:
ygl
*
- nult
L
T
=
.
Various moduli of elasticity
E_L
,
G_LN
and
NU_LN
cannot be selected of
unspecified way: physically, it is necessary always that a nonnull deformation causes one
strictly positive deformation energy. That results in the fact that the matrix of
Hooke must be definite positive. The operator
DEFI_MATERIAU
calculate the eigenvalues of
this matrix and emits an alarm if this property is not checked.
For the models 2D, like the user its MODELING (D_PLAN did not choose yet,
C_PLAN,…), one checks the positivity of the matrix in the various cases of figure.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
26/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
NU_TN = nutn
Poisson's ratio in plan TN.
NU_LN = nuln
Poisson's ratio in plan LN.
The remark made for
NU_LT
is to be applied to these the last two coefficients. One has them thus
relations:
nunt
ygt
ygn
nutn
nunl
ygl
ygn
nuln
=
=
*
*
3.5.3 Operand
RHO
RHO = rho
Density.
3.5.4 Operands
ALPHA_L
/
ALPHA_T
/
ALPHA_N
ALPHA_L = dil
Thermal expansion factor average longitudinal.
ALPHA_T = known as
Thermal expansion factor average transverse.
ALPHA_N = DIN
Thermal expansion factor average normal.
3.5.5 Operands
TEMP_DEF_ALPHA/PRECISION
One will refer to the paragraph [§3.1.4]. This key word becomes obligatory as soon as one informed
ALPHA_L, or ALPHA_T or ALPHA_N.
3.5.6 Criteria of rupture
These various criteria can be used by control CALC_ELEM under the key word
“CRIT_ELNO_RUPT” [U4.81.01], [R4.01.01].
XT = trl
Criterion of rupture in traction in the longitudinal direction (first direction of orthotropism).
TESTSTEMXÇ = neck
Criterion of rupture in compression in the longitudinal direction.
YT = trt
Criterion of rupture in traction in the transverse direction (second direction of orthotropism).
TESTSTEMYÇ = cot
Criterion of rupture in compression in the transverse direction.
S_LT = cis
Criterion of rupture in shearing in plan LT.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
27/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
3.6
Key words factor
ELAS_ISTR
/
ELAS_ISTR_FO
Definition of the constant elastic characteristics or functions of the temperature in the case of
transverse isotropy for the elements of hull and the solid elements isoparametric.
By taking again the same notations as for the orthotropism [§3.4], the transverse isotropy means here,
isotropy in the plan (L, T).
3.6.1 Syntax
/
ELAS_ISTR
=
_F
(
E_L =
ygl, [R]
E_N =
ygn, [R]
G_LN =
gln, [R]
NU_LT =
nult,
[R]
NU_LN =
nuln,
[R]
ALPHA_L =
/dil,
[R]
/
0.0,
[DEFECT]
ALPHA_N =
/DIN,
[R]
/
0.0,
[DEFECT]
RHO =
/rho,
[R]
/
0.0,
[DEFECT]
)
/
ELAS_ISTR_FO
=_F
(
E_L =
ygl, [function **]
E_N =
ygn, [function **]
G_LN =
gln, [function **]
NU_LT =
nult,
[function **]
NU_LN =
nuln,
[function **]
ALPHA_L
=
dil
, [function **]
ALPHA_N
=
DIN
, [function **]
RHO =
/rho,
[R]
/
0.0,
[DEFECT]
TEMP_DEF_ALPHA = Tdef, [R]
PRECISION
=/
,
[R]
/
1.,
[DEFECT]
)
Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
28/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
3.6.2 Operands
of elasticity
The reader will be able to refer to following documentations:
[U4.42.03]
DEFI_COQU_MULT
[U4.42.01]
AFFE_CARA_ELEM
to define a reference mark (L, T, NR) related to the elements and defining the transverse isotropy of material, it
the last being isotropic in plan LT.
Note:
The directions L and T are arbitrary in plan LT.
NR
T
L
L and T define the plan in which
the material is isotropic
E_L = ygl
Young modulus in plan LT.
E_N = ygn
Normal Young modulus.
GL_N = gln
Modulus of rigidity in plan LN.
Note:
The modulus of rigidity in plan LT is defined by the usual formula for materials
isotropic:
(
)
+
= 1
2
E
G
that is to say here
(
)
glt
ygl
nult
=
+
2 1
.
NU_LT = nult
Poisson's ratio in plan LT.
NU_LN = nuln
Poisson's ratio in plan LN.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
29/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
Important remarks:
nult
=
nutl
since the material is isotropic in plan LT, but
nuln
is not
not equal to
nunl
.
One with the relation:
nunl
ygl
ygn
nuln
=
*
nult
must be interpreted in the following way:
if one exerts a traction according to the axis NR giving place to a deformation of traction according to this
axis equalizes with
NR
NR
=
ygn
, there is a compression according to the axis L equalizes with:
nuln
ygn
*
NR
.
Various moduli of elasticity
E_L
,
G_LN
and
NU_LN
cannot be selected of
unspecified way: physically, it is necessary always that a nonnull deformation causes one
strictly positive deformation energy. That results in the fact that the matrix of
Hooke must be definite positive. The operator
DEFI_MATERIAU
calculate the eigenvalues of
this matrix and emits an alarm if this property is not checked.
For the models 2D, like the user its MODELING (D_PLAN did not choose yet,
C_PLAN,…), one checks the positivity of the matrix in the various cases of figure.
3.6.3 Operand
RHO
RHO = rho
Density.
3.6.4 Operands
ALPHA_L
/
ALPHA_N
ALPHA_L = dil
Thermal expansion factor average in plan LT.
ALPHA_N = DIN
Thermal expansion factor average normal.
3.6.5 Operands
TEMP_DEF_ALPHA/PRECISION
One will refer to the paragraph [§3.1.4]. This key word becomes obligatory as soon as the word was informed
key ALPHA_L or ALPHA_N.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
30/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
3.7
Key word factor
ELAS_COQUE
/
ELAS_COQUE_FO
ELAS_COQUE
allows the user to directly provide the coefficients of the matrix of elasticity
(broken up into membrane and bending) of the orthotropic thin hulls in linear elasticity [R3.07.03].
3.7.1 Syntax
/
ELAS_COQUE =
_F (
/ELAS_COQUE_FO
= _F
MEMB_L
=
C1111
,
[R]
or
[function **]
MEMB_LT = C1122, [R]
or
[function **]
MEMB_T
=
C2222
,
[R]
or
[function **]
MEMB_G_LT
= C1212, [R]
or
[function **]
FLEX_L
=
D1111
,
[R]
or
[function **]
FLEX_LT = D1122, [R]
or
[function **]
FLEX_T
=
D2222
,
[R]
or
[function **]
FLEX_G_LT
= D1212, [R]
or
[function **]
CISA_L
=
G11
, [R] or [function **]
CISA_T
=
G22
, [R] or [function **]
RHO
=
rho
, [R] or [function **]
ALPHA
=
alpha
,
[R]
or
[function **]
M_LLLL
=
H1111
,
[R]
or
[function **]
M_LLTT
=
H1111
,
[R]
or
[function **]
M_LLLT
=
H1112
,
[R]
or
[function **]
M_TTTT
=
H2222
,
[R]
or
[function **]
M_TTLT
=
H2212
,
[R]
or
[function **]
M_LTLT
=
H1212
,
[R]
or
[function **]
F_LLLL
=
A1111
,
[R]
or
[function **]
F_LLLL
=
A1111
,
[R]
or
[function **]
F_LLLT
=
A1112
,
[R]
or
[function **]
F_TTTT
=
A2222
,
[R]
or
[function **]
F_TTLT
=
A2212
,
[R]
or
[function **]
F_LTLT
=
A1212
,
[R]
or
[function **]
MF_LLLL = B1111, [R]
or
[function **]
MF_LLTT = B1111, [R]
or
[function **]
MF_LLLT = B1112, [R]
or
[function **]
MF_TTTT = B2222, [R]
or
[function **]
MF_TTLT = B2212, [R]
or
[function **]
MF_LTLT = B1212, [R]
or
[function **]
MC_LLLZ = E1111, [R]
or
[function **]
MC_LLTZ = E1111, [R]
or
[function **]
MC_TTLZ = E1112, [R]
or
[function **]
MC_TTTZ = E2222, [R]
or
[function **]
MC_LTLZ = E2212, [R]
or
[function **]
MC_LTTZ = E1212, [R]
or
[function **]
FC_LLLZ = F1111, [R]
or
[function **]
FC_LLTZ = F1111, [R]
or
[function **]
FC_TTLZ = F1112, [R]
or
[function **]
FC_TTTZ = F2222, [R]
or
[function **]
FC_LTLZ = F2212, [R]
or
[function **]
FC_LTTZ = F1212, [R]
or
[function **]
C_LZLZ
=
G1313
,
[R]
or
[function **]
C_TZTZ
=
G2323
,
[R]
or
[function **]
C_TZTZ
=
G1323
,
[R]
or
[function **]
)

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
31/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
The matrix of behavior intervening in the matrix of rigidity in isotropic homogeneous elasticity
is form:
(
)
(
)
Membrane:
Bending:
Shearing:
1
0
1
1 0
0 0
1
2
1
0
1
1 0
0 0
1
2
1 0
1
0 1
2
2
C
Eh
D
Eh
12
G
5Eh
12
3
= -
-
=
-
-
=
+
For the orthotropic hulls whose moduli of elasticity are obtained by a method
of homogenization, it is not possible in the general case to find a Young modulus equivalent
Eeq, and an equivalent thickness heq to find the preceding expressions.
The matrices of rigidity are thus given directly in the form:
Membrane:
Bending:
Shearing:
C
C
C
C
C
D
D
D
D
D
G
G
1111
1122 0
1122
2222 0
0
0
1212
1111
1122 0
1122
2222 0
0
0
1212
11 0
0
22
C
D
G
=
=
=
On the other hand, one limits oneself to the cases where the thermal expansion factor is homogeneous isotropic.
These coefficients are to be provided in the local reference mark of the element. It is defined by the key word
ANGL_REP
of
AFFE_CARA_ELEM
[U4.42.01].
Notice concerning the taking into account of transverse shearing following the models of
hulls:
If one wishes to use
ELAS_COQUE
for transverse shearing it is necessarily necessary
to employ DST modeling. If one uses modeling DKT, transverse shearing
will not be taken into account, some are the values of G11 and G22. Correspondence for one
isotropic material is as follows:
·
The material
ELAS_COQUE
, DST modeling with CISA_ * = 5/12 * (Eh/(1+nu)) is equivalent
with material
ELAS
, DST modeling.
·
The material
ELAS_COQUE
, DST modeling with CISA_ * = 5/12 * (Eh/(1+nu))* NR, where NR is one
great number (for example 10
5
), is equivalent to the material ELAS, modeling DKT.
·
The material
ELAS_COQUE
, modeling DKT is equivalent to material
ELAS
, modeling
DKT.
Matrices of behavior connecting the efforts generalized to the deformations for the elements of
plate and fascinating account the terms of coupling are in the following way defined:
Membrane:
Bending:
Membrane
bending:
Membrane shearing:
Bending - shearing:
Shearing:
-
=
=
=
=
=
=
H
H
H
H
H
H
With
With
With
With
With
With
B
B
B
B
B
B
E
E
E
E
E
E
F
F
F
F
F
F
G
G
G
G
1111
1122
1112
0
2222
2212
0
0
1212
1111
1122
1112
0
2222
2212
0
0
1212
1111
1122
1112
0
2222
2212
0
0
1212
1113
1123
2213
2223
1213
1223
1113
1123
2213
2223
1213
1223
1313
1323
1323
2323
HM
HF
HMF
HMC
HFC
HC

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
32/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
4
General nonlinear mechanical behaviors
In general, the definition of a nonlinear mechanical behavior requires on the one hand the definition
elastic properties and in addition those relating to the nonlinear aspect itself.
In Code_Aster, these 2 types of data are separately defined, except some exceptions.
4.1
Key word factor
TRACTION
Definition of a traction diagram (elastoplasticity of von Mises with nonlinear isotropic work hardening
or nonlinear elasticity).
4.1.1 Syntax
|
TRACTION = _F
(
SIGM
=
sigm_f
,
[function ***]
)
4.1.2 Operand
SIGM
SIGM = sigm_f
Curve
according to (one checks that the concept function depends many only parameters
EPSI
and possibly
TEMP
).
The ordinate of the first point defines the yield stress of material, it is thus imperative of not
to define of point of null X-coordinate.
Note:
For multiphase materials, the characteristics of work hardening are defined by
META_ECRO_LINE or META_TRACTION.
4.2
Key words factor
ECRO_LINE
/
ECRO_LINE_FO
Definition of a linear curve of work hardening or a whole of curves depending on
temperature.
4.2.1 Syntax
|
ECRO_LINE = _F
(
D_SIGM_EPSI
=
dsde, [R]
SY
= sigm,
[R]
)
|
ECRO_LINE_FO
=_F
(
D_SIGM_EPSI
=
dsde, [function **]
SY
= sigm,
[function **]
)
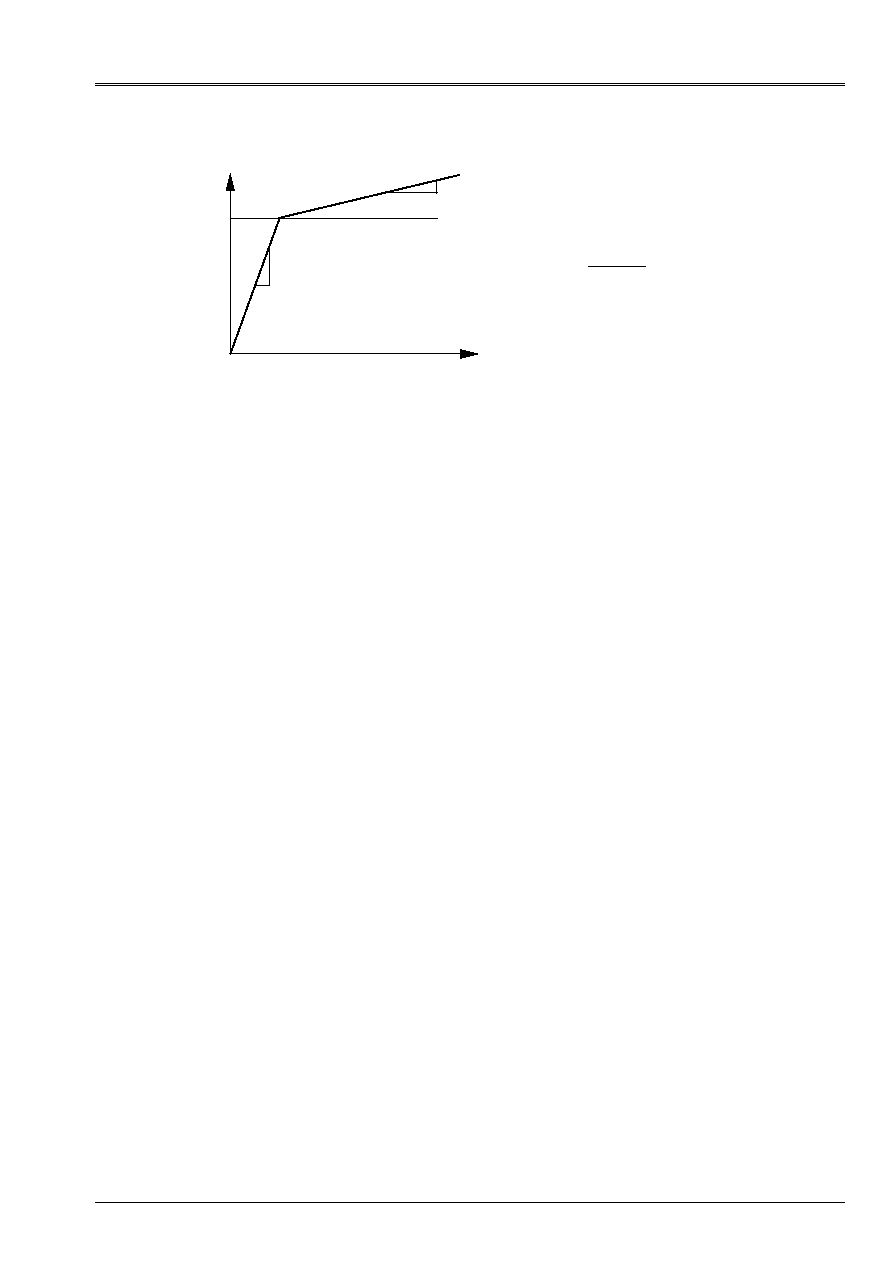
4.2.2 Operands
D
_
SIGM_EPSI = dsde (AND)
Slope of the traction diagram.
SY = sigm
Elastic limit.
Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
33/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
sigm
E
1
E
T
The curve of work hardening used in
models of behavior is then:
()
R p
H
y
p
=
+
with
H
E E
E E
T
T
=
-
.
It is thus necessary to respect:
E
E
T
<
The Young modulus E is to be specified by the key words
ELAS
or
ELAS_FO
.
4.3
Key words factor PRAGER/PRAGER_FO
When the way of loading is not monotonous any more, work hardenings isotropic and kinematic are not
more equivalent. In particular, one can expect to have simultaneously a kinematic share and one
isotropic share. If one seeks to precisely describe the effects of a cyclic loading, it is
desirable to adopt modelings sophisticated (but easy to use) such as the model of
Taheri, for example, cf [R5.03.05]. On the other hand, for less complex ways of loading,
one can wish to include only one linear kinematic work hardening, all nonthe linearities of
work hardening being carried by the isotropic term. That makes it possible to follow a curve precisely of
traction, while representing nevertheless phenomena such as the Bauschinger effect [R5.03.16].
The characteristics of work hardening are then given by a traction diagram and a constant,
said of Prager, for the term of kinematic work hardening linear. Key word PRAGER makes it possible to define
the constant of PRAGER, used in the models with mixed work hardening (kinematic linear compound
with isotropic) VMIS_ECMI_LINE or VMIS_ECMI_TRAC.
4.3.1 Syntax
|
PRAGER = _F
(
C = C, [R]
)
|
PRAGER_FO = _F
(
C = C, [function **]
)
The identification of C is described in [R5.03.16].

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
34/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
4.4 Word
key
CHABOCHE
Behavior of the model of Chaboche describes in the document [R5.03.04].
Briefly these relations are:
(
)
()
(
)
(
)
()
& &
~
~
&
&
&
-
-
-
=
-
-
-
-
=
-
X
X
R p
p
X
X
X
X
X
C
has
p
X p
eq
p
I
I
I
p
I
1
2
1
2
1
2
0
3
2
2
3
eq
éq
4.4-1
with:
()
(
)
()
(
)
R p
R
R
R E
p
K
E
LP
wp
=
+
-
=
+
-
-
-
0
1
1
and of the conventional relations of plasticity.
Note:
~
represent the diverter of the stresses and ()
eq
the equivalent within the meaning of von Mises.
This model does not make it possible to take into account the variation of the coefficients with
temperature.
With this intention, it is necessary to use VMIS_CIN1_CHAB_FO or VMIS_CIN2_CHAB_FO.
4.4.1 Syntax
|
/CHABOCHE = _F
(
R_I
=
Rinfi,
[R]
R_0
=
Rzero,
[R]
B =
B,
[R]
K =
K,
[R]
W =
W,
[R]
A1 =
a1, [R]
A2 =
a2, [R]
C1 =
C1, [R]
C2 =
C2, [R]
)

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
35/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
4.5
Key words factor
CIN1_CHAB
/
CIN1_CHAB_FO
Behavior of the model of Chaboche (news version with only one kinematic variable) described
in the document [R5.03.04].
Briefly these relations are:
(
)
(
)
()
F,
~
R
R p
eq
X
X
=
-
-
(
)
&
& F
& ~
~
p
X
X
=
=
-
-
3
2
eq
&
&
&
&
p
= =
2
3
p
p
:
éq 4.5-1
if
or
if
and
F
&F
&
F
&F
&
<0
0
0
0
0
0
<
=
=
=
éq
4.5-2
()
()
X
p
,
& &
&
=
=
-
2
3 C p
p
p
éq
4.5-3
Functions
() ()
C p
p
and
()
R p
are defined by:
()
(
)
()
(
)
(
)
R p
R
R
R E
C p
C
K
E
LP
wp
=
+
-
=
+
-
-
-
0
1
1
()
(
)
(
)
1
0
1
p
has
E has
LP
=
+ -
-
Note:
~
represent the diverter of the stresses and ()
eq
the equivalent within the meaning of von Mises.
The definition of
X
in the form [éq 4.5-3] allows to keep a formulation which takes in
count the variations of the parameters with the temperature. These terms are necessary because them
not taken into account would lead to inaccurate results.
4.5.1 Syntax
CIN1_CHAB (CIN1_CHAB_FO)
= _F (
R_0 =
R_0
,
[R]
or
[function **]
R_I
= R_I, (useless if B=0) [R] or [function **]
B =
B
, (defect: 0.)
[R] or [function **]
C_I =
C_I,
[R]
or
[function **]
K =
K
, (defect: 1.)
[R] or [function **]
W =
W
, (defect: 0.)
[R] or [function **]
G_0
=
G_0,
[R]
or
[function **]
A_I
= A_I, (defect: 0.)
[R] or [function **]
)
Note:
A viscoplastic version of the model of Chaboche to a true kinematics is also
available (cf [R5.03.04]). It requires to define viscous characteristics using
key word factor LEMAITRE or LEMAITRE_FO, by putting parameter UN_SUR_M obligatorily
to zero.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
36/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
4.6
Key words factor
CIN2_CHAB
/
CIN2_CHAB_FO
Behavior of the model of Chaboche (news version with two variables kinematics) described in
the document [R5.03.04].
Briefly these relations are:
(
)
(
)
()
F,
~
R
R p
eq
X
X
X
=
-
-
-
1
2
(
)
&
& F
& ~
~
p
X
X
X
X
=
=
-
-
-
-
3
2
1
2
1
2 eq
&
&
&
&
p
= =
2
3
p
p
:
éq 4.6-1
if
or
if
and
F
&F
&
F
&F
&
<0
0
0
0
0
0
<
=
=
=
éq 4.6-2
()
()
()
()
X
X
p
p
1
1
2
2
1
2
2
3
2
3
,
,
&
&
&
&
&
&
=
=
=
-
=
-
C p
C p
p
p
p
p
1
2
1
1
2
2
éq 4.6-3
Functions
() () () ()
C PC p
p
p
1
2
1
2
and
()
R p
are defined by:
()
(
)
()
(
)
(
)
()
(
)
(
)
R p
R
R
R E
C p
C
K
E
C p
C
K
E
LP
wp
wp
=
+
-
=
+
-
=
+
-
-
-
-
0
1
1
2
2
1
1
1
1
()
(
)
(
)
()
(
)
(
)
1
1
0
2
2
0
1
1
p
has
E has
p
has
E has
LP
LP
=
+ -
=
+ -
-
-
Note:
~
represent the diverter of the stresses and ()
eq
the equivalent within the meaning of von Mises.
The definition of
X
1
and
X
2
in the form [éq 4.5-3] allows to keep a formulation which takes in
count the variations of the parameters with the temperature. These terms are necessary because them
not taken into account would lead to inaccurate results.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
37/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
4.6.1 Syntax
CIN2_CHAB (CIN2_CHAB_FO)
= _F (
R_0 =
R_0,
[R]
or
[function **]
R_I
= R_I, (useless if B=0) [R] or [function **]
B =
B
, (defect: 0.)
[R] or [function **]
C1_I =
C1_I,
[R]
or
[function **]
C2_I =
C2_I,
[R]
or
[function **]
K = K,
(defect
:
1.)
[R] or [function **]
W = W,
(defect
:
0.)
[R] or [function **]
G1_0 =
G1_0,
[R]
or
[function **]
G2_0 =
G2_0,
[R]
or
[function **]
A_I
=
A_I, (defect:
0.)
[R] or [function **]
)
Note:
A viscoplastic version of the model of Chaboche with two variables kinematics is
also available (cf [R5.03.04]). It requires to define characteristics
viscous using the key word factor LEMAITRE or LEMAITRE_FO, while putting
obligatorily parameter UN_SUR_M to zero.
4.7
Key words factor
TAHERI
/
TAHERI_FO
Definition of the coefficients of the model of cyclic behavior of elastoplasticity of Said Taheri
[R5.03.05].
Briefly we have to solve, for an elastoplastic increment:
(
)
()
(
)
(
)
(
)
(
)
(
)
()
}
& & ~
~
& &
/
.
p
eq
eq
T
p
p
p pn
eq
p
T
eq
p
eq
p
X
X
with X
X X
R
D WITH
R
X
C S
X
R
X
R
R
X
D
=
-
-
=
=
+
=
-
=
-
-
-
=
=
+
-
-
=
=
3
2
3
2
0
0
1
1 2
0
Max
&
-
=
=
+
-
-
-
-
me
C
C
C E
LP
S
p
N
LP
S
p
p
1
1
1
0
where the various parameters of material are
S C
C B m A
and R
,
,
,
,
.
,
1
0
The various parameters can depend on the temperature, in this case one will employ the key word
TAHERI_FO
.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
38/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
4.7.1 Syntax
|
/
TAHERI
=
_F
(
R_0
= R, [R]
ALPHA =
, [R]
M = m, [R]
WITH = A, [R]
B = B, [R]
C1
=
C1
,
[R]
C_INF = Cinfi,
[R]
S = S, [R]
)
/
TAHERI_FO
=
_F
(
R_0
= R, [function **]
ALPHA =
, [function **]
M = m, [function **]
With = A, [function **]
B = B, [function **]
C1
=
C1
,
[function **]
C_INF = Cinfi,
[function **]
S = S, [function **]
)
Note:
A viscoplastic version of the model of TAHERI is also available (cf [R5.03.05]).
It requires to define viscous characteristics using the key word factor
LEMAITRE or LEMAITRE_FO.
4.7.2 Syntax
|
/OHNO:
/
OHNO_FO: _F (
R_0:
R0
[R]
or [function **]
R_I:
R
inf
[R]
or [function **]
PHI:
phi_inf
[R]
or [function **]
B: B [R]
or [function **]
A1
:
C1
[R]
or [function **]
A2
:
C2
[R]
or [function **]
A3
:
C3
[R]
or [function **]
A4
:
C4
[R]
or [function **]
A5
:
C5
[R]
or [function **]
GAMMA1
:
G
1
[R]
or [function **]
GAMMA2
:
g2
[R]
or [function **]
GAMMA3
:
g3
[R]
or [function **]
GAMMA4
:
g4
[R]
or [function **]
GAMMA5
:
g5
[R]
or [function **]
M1
:
m1
[R]
or [function **]
M2
:
m2
[R]
or [function **]
M3
:
m3
[R]
or [function **]
M4
:
m4
[R]
or [function **]
M5
:
m5
[R]
or [function **]
)

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
39/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
4.8
Key word factor
POLY_CFC
/
POLY_CFC_FO
Definition of the coefficients of the model of polycrystalline behavior of the School of the Mines of Paris
[R5.03.13]. In addition to these characteristics, constant the rubber bands must be defined under the word
key ELAS by the real coefficients or ELAS_FO by the coefficients depending on the temperature.
Total behavior: definition of the deformations on a point scale of Gauss
“
“
N
orientatio
of
granulates
of
proportion
G
F
F
G
G
vp
ij
G
vp
ij
vp
ij
HT
ij
E
ij
ij
G
:
+
+
=
=
Intragranular behavior:
(
)
&
&
ij
vp
S
S G
ijs
I
J
J
I
G
m
N
L
L
N
=
=
+
m
ijs
1
2
&
|
& |
p
F
K
S
S
S N
=
=
with <x>=0 if x<0 and <x>=x if x>0
Criterion:
()
2
0
2
1
S
S
S
S
S
X
D
C
R
X
F
+
-
-
-
=
S
G
m
=
ij
ijs
:
X
C
X
S
S
S
=
+
=
+
S
S
has
has
&
&
&
S
S
p
=
-
S
S
D
R
H Q
Q
S
rs
R S
S
S
= Q
Q
1
2
(
)
+
1
2
(
)
(
)
S
R
S
R
H
H
I
p
Q
B
Q
rs
rs
rs
rs
rs
S
is
I
is
=
=
=
+
-
=
=
-
if
and
if
with
)
=
0
1
1
2
,
1
1
(
&
&
Relations of scaling
(
)
G
G
G
vp
ij
vp
ij
G
ij
vp
ij
G
ij
G
G
ij
G
ij
G
ij
ij
G
ij
D
F
B
E
B
ij
µ
µ
&
&
&
-
-
=
=
+
=
-
+
=
1
2
1
where the various parameters of material are:
D
N K
Q
H Q
C D has
,
,
,
,
0
1
2
, B,
, B,
1
2
.
various parameters can depend on the temperature, in this case one will employ the key word
POLY_CFC_FO
.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
40/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
4.8.1 Syntax
The model is accessible in Code_Aster in 3D, plane deformations (
D_PLAN
), forced
plane (
C_PLAN
) and axisymmetric (
AXIS
) starting from the key word
COMP_INCR
control
STAT_NON_LINE
. The whole of the parameters of the model is provided under the key word factor
POLY_CFC
or
POLY_CFC_FO
:
/
POLY_CFC
=
_F
(
DLL
=
D,
[R]
DA
=
delta,
[R]
NR
=
N,
[R]
K
=
K,
[R]
TAU_0 =
tau
0,
[R]
Q1
= Q1,
[R]
B1
= b1,
[R]
HL
=
H,
[R]
Q2
= Q2,
[R]
B2
= b2,
[R]
C1
=
C,
[R]
D1
=
D,
[R]
C2
=
has,
[R]
)
/
POLY_CFC_FO
=_F
(
DLL
=
D,
[function **]
DA
=
delta,
[function **]
NR
=
N,
[function **]
K
=
K,
[function **]
TAU_0 =
tau
0,
[function **]
Q1
= Q1,
[function **]
B1
= b1,
[function **]
HL
=
H,
[function **]
Q2
= Q2,
[function **]
B2
= b2,
[function **]
C1
=
C,
[function **]
D1
=
D,
[function **]
C2
=
has,
[function **]
)

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
41/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
4.9 Key words factors
ECOU_VISC1
,
ECOU_VISC2
,
ECOU_VISC3
,
ECRO_CIN1
,
ECRO_CIN2
,
ECRO_ISOT1
,
ECRO_ISOT2
Definition of the coefficients of the models of single-crystal or polycrystalline behavior [R5.03.11]. In
more these characteristics, constant the rubber bands must be defined under key word ELAS or
ELAS_ORTH
for the real coefficients or ELAS_FO for the coefficients depending on the temperature.
The behavior related to each system of slip of a monocrystal or a phase of a polycrystal
is (in the whole of the behaviors considered) of élasto-visco-plastic type. Owing to the fact that one
be interested each time in only one direction of slip, the behavior is mono
dimensional. It can break up into 3 types of equations:
· relation of flow:
(
)
S
S
S
S
S
p
G
,
,
,
=
· evolutions of kinematic work hardening:
(
)
S
S
S
S
S
p
H
,
,
,
=
· evolution of isotropic work hardening:
()
S
S
p
R
, with
S
S
p
=
The relation of flow ECOU_VISC1 is:
(
)
S
S
S
S
S
p
G
,
,
,
=
=
()
S
S
S
S
N
S
S
S
S
C
C
K
p
R
C
-
-
-
-
.
, the parameters are: C, K, N
The relation of flow ECOU_VISC2 is:
(
)
S
S
S
S
S
p
G
,
,
,
=
=
()
()
S
S
S
S
S
S
N
S
S
S
S
S
S
has
C
has
C
K
C
D
C
p
R
has
C
-
-
-
-
+
-
-
-
.
2
2
,
the parameters are then: C, K, N, has, D
The relation of flow ECOU_VISC3 is:
(
)
S
S
S
S
S
p
G
,
,
,
=
=
S
S
S
kT
V
kT
G
µ
.
exp
exp
*
0
*
0
-
-
&
,
the parameters are: K, Boltzmann constant, in eV/K,
,
µ
Threshold of flow (homogeneous to one
stress),
*
0
&
Initial rate of flow,
*
V
Volume of activation,
0
G
Gain of bound energy on
crossing of obstacle.
Kinematic work hardening can be form ECRO_CIN1:
(
)
S
S
S
S
S
S
S
S
p
D
p
H
-
=
=
.
.
,
,
,
, with for parameter:
D
or ECRO_CIN2:
(
)
S
S
m
S
S
S
S
S
S
S
S
S
M
C
p
D
p
H
-
-
=
=
.
.
,
,
,
, parameters being then:
D
,
M
and
m
Isotropic work hardening can for example be form ECRO_ISOT1
()
(
)
(
)
Sr
Sr
Sr
NR
R
LP
Sr
S
S
H
H
E
H
Q
R
p
R
R
+
-
=
-
+
=
=
-
1
with
1
1
0
, the parameters are H, Q, R
0
, B
Or ECRO_ISOT2:
()
(
)
dp
Q
B
dq
Q
Q
Q
H
Q
R
p
R
is
I
is
S
sg
S
rs
S
.
1
with
,
2
2
1
1
0
-
=
+
+
=
the parameters are H, Q
1
, Q
2
, B
1
, B
2
,
R
0
.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
42/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
4.9.1 Syntax
These relations are accessible in Code_Aster in 3D, plane deformations (
D_PLAN
), forced
plane (
C_PLAN
) and axisymmetric (
AXIS
) starting from the key word
COMP_INCR
control
STAT_NON_LINE
. The choice of the relations allowing to build the model of behavior of
monocrystal is carried out via the operator
DEFI_COMPOR
[U4.43.05].
ECOU_VISC1
=
_F
(
C = C [R]
K =
K,
[R]
NR
=
N,
[R]
)
ECOU_VISC1
=
_F
(
C = C [R]
K =
K,
[R]
NR
=
N,
[R]
With =
K,
[R]
D
=
N,
[R]
)
ECOU_VISC3
=
_F
(
K
=
K
[R]
TAUMU =
µ
[R]
GAMMA0
=
*
0
&
[R]
DELTAV
=
*
V
[R]
DELTAG0=
0
G
[R]
)
ECRO_ISOT1
=_F (
R_0
=
R [R]
Q
=
Q,
[R]
B
=
B
[R]
H
=
H
[R]
),
ECRO_ISOT2 =_F (
R_0
=
R0
[R]
Q1
=
Q1
[R]
B1
=
b1
[R]
H
=
H
[R]
Q2
=
Q2 [R]
B2
=
b2 [R]
),
ECRO_CINE1
=_F (
D
=
D
[R]),
),
ECRO_CINE2
=_F (
D
=
D
[R]
GM
=
M
[R]
PM
=
m
[R]
C
=
C
[R]
)

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
43/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
4.10 Key words factor
LEMAITRE
/
LEMAITRE_FO
Definition of the coefficients of the non-linear relation of viscoplasticity of Lemaitre [R5.03.08].
The equations are as follows:
(
)
-
=
=
=
v
N
m
eq
eq
ij
v
ij
p
K
p
p
/
1
1
~
2
3
&
&
&
The coefficients to be introduced are:
N
K
m
>
0 1
1
0
,
.
and
4.10.1 Syntax
/
LEMAITRE
=
_F
(
NR
=
N,
[R]
UN_SUR_K
= 1/K
, [R]
UN_SUR_M =
/1/m, [R]
/
0.0,
[DEFECT]
)
/
LEMAITRE_FO
=
_F
(
NR
=
N,
[function]
UN_SUR_K
= 1/K
, [function]
UN_SUR_M =
1/m, [function]
)
NR:
N
UN_SUR_K:
1/K
UN_SUR_M:
1/m
If it is wished that the behavior depend on the fluence (description of
behavior of the fuel assemblies by ASSE_COMBU in STAT_NON_LINE), it is necessary
to also inform two key words GRAN_IRRA and FLU_IRRA (cf [§11] of this document).
Note:
While taking
(
)
+
=
=
m
m
IE
0
1
, i.e. by putting 0. behind the operand
UN_SUR_M
, one
a non-linear relation of viscoelasticity of Norton obtains.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
44/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
4.11 Key word factor VISC_SINH
Definition of the coefficients of the law of viscosity defined by the following viscoplastic potential:
The equation defining the rate of cumulated plastic deformation is thus the following one:
,
0
0
m
p
HS
p
>
<
=
&
&
expression in which
>
< X
indicate the positive part of
p
X
and
the plastic threshold.
This model of viscosity is available:
· with the model of Rousselier version
PETIT_REAC
: law of behavior
ROUSS_VISC
· with the models of plasticity
VMIS_ISOT_TRAC
and
VMIS_ISOT_LINE
version
SIMO_MIEHE
: laws of behavior
VISC_ISOT_TRAC
and
VISC_ISOT_LINE
.
The coefficients to be introduced are:
.
0
,
,
0
0
>
and
&
m
4.11.1 Syntax
/
VISC_SINH
=
_F
(
M
=
m,
[R]
EPSI_0
=
0, [R]
SIGM_0
=
0,
[R]
)
-
=
-
m
p
HS
p
vp
1
0
1
0
&
&

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
45/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
4.12 Word
key
LEMA_SEUIL
Definition of the coefficients of the non-linear relation of viscoplasticity of Lemaitre with threshold
[R5.03.08]. One places oneself on the assumption of the small disturbances and one divides the tensor of
deformations in an elastic part, a thermal part, a anelastic part (known) and one
viscous part. The equations are then:
()
(
)
eq
eq
v
E
v
has
HT
E
early
T
G
T
~
2
3
,
,
=
=
+
+
+
=
&
With
with:
: cumulated viscous deformation
v
v
&
&
&
:
3
2
=
~
: diverter of the stresses
()
I
Tr
3
1
~
-
=
eq
: equivalent stress
~
:
~
2
3
=
eq
()
T
With
: tensor of elasticity
and:
if
1
D
then
(
)
0
,
,
=
T
G
(purely elastic behavior)
if
1
>
D
then
(
)
0
,
0
3
2
,
,
=
With
With
T
G
with
With:
()
=
T
eq
U
S
D
0
1
The data materials to be informed by the user are
With
and
S
.
As for the parameter
, it is about the flow of neutrons which bombards material. It must be indicated
under the key word factor VARI_COMM of control STAT_NON_LINE.
The Young modulus
E
and the Poisson's ratio
v
are those provided under the key words factors
ELAS or ELAS_FO.
4.12.1 Syntax
/
LEMA_SEUIL
=
_F
(
With
=
With,
[R]
S
=
S,
[R]
)
/
LEMA_SEUIL_FO
=
_F
(
With
=
With,
[function]
S
=
S,
[function]
)

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
46/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
4.13 Key word factor
ZIRC_CYRA2
Definition of the coefficients of the non-linear relation of viscoelasticity of Zircaloy used in the code
CYRANO3. This relation corresponds to a unidimensional creep test, constant stress,
who utilizes the time passed since the moment when the stress is applied. Generalization 3D and
a formulation eliminating time were introduced into Code_Aster (cf [R5.03.08]).
The formulation is as follows:
()
(
)
() ()
()
(
)
()
[
]
v
K
T
T
fab
fab
With E
F T
T G
H T
F T
T G
rec
=
+
+
+
+
0
1
1
1
2
2
with
T
time in hours,
T
the temperature (in °C) of the point considered and
the stress (in MPa).
This imposes that the mesh is in millimetre.
and where
WITH K T
F G H F G
,
,
0
1
1 1 2
2
and
are respectively fixed constants and functions and
defined once and for all in the code, where the only coefficients to be introduced are:
T
rec
:
temperature of annealing (°C)
fab
:
deformation of creep measured after a biaxal test of creep with (400°C, 100MPa, 250 hours)
: flux neutron (neutrons/cm
2
/S)
Note:
The effects of isotropic thermal dilation can be taken into account if the parameters
of elasticity were defined under key word ELAS or ELAS_FO.
4.13.1 Syntax
/
ZIRC_CYRA2
=
_F
(
EPSI_FAB =
E
fab
,
[R]
TEMP_RECUIT
=
Trec
,
[R]
FLUX_PHI
= phi,
[R]
)
4.14 Key word factor
ZIRC_EPRI
Definition of the coefficients of the non-linear relation of viscoelasticity of Zircaloy used in
program ESCORE of the EPRI. This relation corresponds to a unidimensional creep test, with
constant stress, and which utilizes the time passed since the moment when one applies the stress.
Generalization 3D and a formulation eliminating time was introduced into Code_Aster
(cf [R5.03.08]).
The formulation is as follows:
() () ()
()
() () ()
()
(
)
v
p
has
p
B
C
D
F T G
H T R
F T G
H T R
=
+
3
3
3
4
4
4
cos
max
with
T
time in hours,
T
the temperature (in °C) of the point considered and
the stress (in MPa).
and where
B C D has
F G H F G H
,
,
and
3
3
3
4
4
4
are respectively fixed constants and functions and
defined once and for all in the code, where the coefficients to be introduced are:
R
p
:
yield stress (MPa)
max
: the angle of the basic plan of the crystals with a radial direction with the sheath (rad) such as
0
2
<
max
: flux neutron (neutrons/cm
2
/S)

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
47/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
Note:
The effects of isotropic thermal dilation can be taken into account if the parameters
of elasticity were defined under key word ELAS or ELAS_FO.
4.14.1 Syntax
/
ZIRC_EPRI
=_F
(
FLUX_PHI =
phi,
[R]
R_P = RP,
[R]
THETA_MAX
=
theta_
max,
[R]
)
4.15 Key word factor
VISC_IRRA_LOG
Definition of a law of axial creep under irradiation of the tubes guides. This law consists of a law
of primary education type and a secondary law in logarithm of the fluence (cf [R5.03.08]).
The formulation is as follows:
(
)
T
T
Q
B
T
T
Q
With
F
.
.
exp
.
.
1
ln
.
.
exp
.
-
+
+
-
=
F
:
axial deformation of creep
Q
:
energy of activation
T
:
temperature of activation (in °K)
:
axial stress applied to the tube guides
T
:
neutron flux (10
+20
neutrons/cm
2
)
:
time-constant
B
With,
constants
4.15.1 Syntax
/
VISC_IRRA_LOG
=_F (
With =
/1.28D-1, [DEFECT]
/
has,
[R]
B
=
/
0.01159,
[DEFECT]
/
B,
[R]
FLUX_PHI
=
phi,
[R]
CSTE_TPS = W,
[R]
ENER_ACT =
Q
, [R]
)

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
48/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
4.16 Key words factor
LMARC
/
LMARC_FO
Definitions of the coefficients of the élasto-viscoplastic model developed with the LMA-RC to describe it
orthotropic viscoplastic behavior of the tubes of sheaths of the fuel pin [R5.03.10].
Briefly, the relations of behavior are:
(
)
(
)
(
)
()
()
()
(
)
()
F
X
X M
X
F
M
X
X
M
X
X
NR
Q X X
X
X
X
X
=
-
-
=
-
-
=
=
-
-
=
=
-
=
-
-
-
-
~
~
~
&
&v
&v
~
~
&v
&
&
& sin
~
&
v
&
&v
sinh
v
v
v
v
R
H
K
p
Y
R
X
NR R
T
p
p T
p
N
p
m
m
0
1
0
1
0
1
3
2
3
2
2
3
2
3
()
()
()
(
)
()
()
()
=
-
-
=
-
p
Y
p
Y
p
p
1
1
2
2
2
2
2
3
2
3
v
&
&v
v
&
&v
v
v
NR
Q X
X
X
NR
Q X
with:
()
(
)
Y
Y
Y
Y
E
NR
B
T
v
v
=
+
-
=
0
3
2
X
X
X
Note:
~
represent the diverter of the stresses and
~
- X
the equivalent within the meaning of Hill.
Matrices
MR. NR R
Q
,
and
allow to describe the anisotropy of behavior
viscoplastic.
4.16.1 Syntax
|
/LMARC
=
|
/LMARC_FO = _F
(
R_0
= R0
, [R] or [function **]
DE_0 =
eps
0, [R] or [function **]
NR =
N
,
[R] or [function **]
K =
K
,
[R] or [function **]
Y_0
=
y0
,
[R] or [function **]
Y_I
=
yinfi,
[R] or [function **]
B =
B
,
[R] or [function **]
A_0
= X0,
[R] or [function **]
RM
= rm,
[R] or [function **]
M =
m
,
[R] or [function **]
P =
p
,
[R] or [function **]
P1
= p1,
[R] or [function **]
P2
= p2,
[R] or [function **]
M11
= M11,
[R] or [function **]
M22
= M22,
[R] or [function **]
M33
= M33,
[R] or [function **]
M66
= M66,
[R] or [function **]
N11
= N11,
[R] or [function **]
N22
= M22,
[R] or [function **]
N33
= N33,
[R] or [function **]
N66
= N66,
[R] or [function **]
Q11
= Q11,
[R] or [function **]
Q22
= Q22,
[R] or [function **]
Q33
= Q33,
[R] or [function **]
Q66
= Q66,
[R] or [function **]
R11
= R11,
[R] or [function **]
R22
= R22,
[R] or [function **]
R33
= R33,
[R] or [function **]
R66
= R66,
[R] or [function **]
)

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
49/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
5
Behaviors related to the damage and the rupture
5.1
Key words factor
ROUSSELIER
/
ROUSSELIER_FO
Definition of the coefficients of the model of ductile behavior of rupture of G. Rousselier
(cf [R5.03.06]).
Briefly, one solves for an elastoplastic increment:
()
(
)
(
)
-
=
=
-
=
=
+
-
-
1
3
0
exp
1
1
p
H
p
p
H
eq
F
F
F
p
F
D
p
R
&
&
&
1
5.1
éq
with
()
1
1
exp
3
~
2
3
1
TRACTION)
0
1
-
-
=
+
=
-
identity
stamp
key
(word
traction
of
curve
of
anger
intermédia
by
input
I
2
5.1
éq
p
R
F
F
Df
F
H
eq
With the coefficients materials
D
F
,
1
0
specific to the model of ROUSSELIER.
These various parameters can depend on the temperature, in this case one will employ the key word
ROUSSELIER_FO
.
It is possible to modify the model in the following way:
·
introduction of a critical porosity
F
C
beyond which the growth of the cavities is
accelerated:
C
p
H
F
F
F
With
F
>
-
=
if
)
1
(
3
&
two additional characteristics are then necessary:
F
With
C
and
.
·
introduction of a limiting porosity
F
L
beyond which the material is considered broken.
behavior is then replaced by an imposed fall of the stresses:
)
(
ELAS
under
defined
with
if
E
F
F
E
L
=
-
=
&
&
two additional characteristics are then necessary:
F
1
and
.
·
introduction of a voluminal rate of germination of fissures of cleavages
N
With
, modifying
as follows the equations [éq 5.1-1] and [éq 5.1-2].
()
(
)
-
-
-
=
=
+
+
-
0
1
1
1
1
0
exp
F
p
With
F
p
With
F
D
p
R
N
H
N
eq

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
50/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
These last five parameters are independent of the temperature.
The following table of correspondence must be used:
Modeling Key words
D
D
1
SIGM_1
F
0
PORO_INIT
F
C
PORO_CRIT
With
PORO_ACCE
N
With
YEAR
F
L
PORO_LIMI
D_SIGM_EPSI_NORM
5.1.1 Syntax
|
/ROUSSELIER = _F (
D = D, [R]
SIGM_1
=
1
,
[R]
PORO_INIT
= f0
, [R]
PORO_CRIT
=/1.D0, [DEFECT]
/
FC
,
[R]
PORO_ACCE
=/1.D0, [DEFECT]
/
With,
[R]
YEAR
=
/
0.D0,
[DEFECT]
/
Year,
PORO_LIMI
=/0.999,
[DEFECT]
/
fl
,
[R]
D_SIGM_EPSI_NORM=/1.D0,
[DEFECT]
/
,
[R]
)
/
ROUSSELIER_FO=_F
(
D = D, [function **]
SIGM_1
=
1
,
[function **]
PORO_INIT
= f0
, [function **]
PORO_CRIT
=/1.D0,
[DEFECT]
/FC
,
[R]
PORO_ACCE
=/1.D0,
[DEFECT]
/A
,
[R]
YEAR
=
/
0.D0,
[DEFECT]
/
Year,
PORO_LIMI
=/0.999
, [DEFECT]
/fl
,
[R]
D_SIGM_EPSI_NORM=/1.D0,
[DEFECT]
/
, [R]
)
Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
51/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
5.2 Words
keys
VENDO_CHAB
/
VENDO_CHAB_FO
Definition of the coefficients of the viscoplastic law of behavior with damage of
Chaboche (makes of it law of viscoplastic behavior to work hardening-viscosity multiplicative coupled to
the isotropic, model damage developed by Chaboche cf [R5.03.15]).
Briefly, the relations are:
(
)
(
)
(
)
(
)
()
(
)
()
()
-
=
-
-
-
=
-
=
=
-
-
=
-
=
-
K
R
NR
M
eq
eq
p
p
HT
E
E
D
With
D
R
K
D
D
S
R
D
R
p
p
E
D
1
1
1
1
~
2
3
1
1
&
&
&
&
&
and
with
D
, the scalar variable of isotropic damage and:
()
()
()
(
)
()
=
+
+ - -
J
J
J
0
1
2
1
where:
()
() ()
()
J
J
Tr
J
eq
0
1
2
is the maximum main stress
=
=
X
: positive part of
X
Note:
~
represent the diverter of the stresses and
eq
the equivalent stress of Von Mises.
5.2.1 Syntax
|
/VENDO_CHAB:
/
VENDO_CHAB_FO
: _F (
S_VP: [R]
or [function **]
SEDVP1:
[R] or [function **]
SEDVP2:
[R] or [function **]
N_VP: [R]
or [function **]
M_VP: [R]
or [function **]
K_VP: [R]
or [function **]
A_D:
[R]
or [function **]
R_D:
[R]
or [function **]
K_D:
[R]
or [function **]
)

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
52/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
The table below summarizes the correspondences between the symbols of the equations and the words key
of Aster.
Parameter material
Symbol in
equations
Key word in Aster
Threshold of viscoplasticity
S
“S_VP”
Coefficient 1 of the equivalent stress of creep
“SEDVP1”
Coefficient 2 of the equivalent stress of creep
“SEDVP2”
First exponent of the viscoplastic law
NR
“N_VP”
Second exponent of the viscoplastic law
M
“M_VP”
Coefficient of the viscoplastic law
K
“K_VP”
Coefficient of the law of damage
With
“A_D'
First exponent of the law of damage
R
“R_D'
Second exponent of the law of damage
[]
[
]
K
“K_D'
Note:
·
“_VP”
: coefficient intervening in an equation of the viscoplastic behavior
·
“_D'
: coefficient intervening in an equation of the behavior of damage
·
“SEDVP”
:
(Sigma) Equivalent in Viscoplastic Damage.
The parameter
K_D
can be defined like a constant, a function of a parameter
“TEMP”
or
a tablecloth (variable of temperature and stress
()
). In this case, to use
DEFI_NAPPE
with like first parameter
“TEMP”
for the temperature in °C and like second parameter
“X”
(obligatory) for the stresses
()
in MPa. If
K_D
depends only on
()
, it is necessary
to use
DEFI_NAPPE
in any event by introducing for example 2 times same data file
in stress for two values different from the temperature.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
53/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
5.3
Key word factor ENDO_ORTH_BETON
Definition of the parameters of the law of behavior ENDO_ORTH_BETON, allowing to describe
anisotropy induced by the damage of the concrete, as well as the unilateral effects [R7.01.09]. One
will defer to the documents [R7.01.09] and [V6.04.176] for the precise significance of the parameters and
procedure of identification.
5.3.1 Syntax
ENDO_ORTH_BETON = _F (
ALPHA
=
/
alpha
[R],
/
0.9
[DEFECT],
K0
=
k0
[R],
K1
=
k1
[R],
K2
=
/
k2
[R],
/
0.0007
[DEFECT]
ECROB
=
ecrob
[R],
ECROD
=
ecrod
[R],
)
5.3.2 Operand
ALPHA
Constant of coupling between the evolution of the damage of traction and that of
the damage of compression. It must be taken between 0 and 1, rather near to 1. The value by
defect is 0.9.
5.3.3 Operands
K0/K1/K2
K0 = k0
Constant part of the function threshold. Allows to gauge the height of the peak in traction.
K1 = k1
Parameter of the function threshold allowing to increase the threshold in compression.
K2 = k2
Parameter of control of the shape of the envelope of rupture for biaxial tests. The value by
defect is 7.10
4
.
5.3.4 Operands
ECROB/ECROD
ECROB = ecrob
Term of locked energy (equivalent to an energy of work hardening) relating to the evolution of
the damage of traction. Allows to control the shape of the peak in traction.
ECROD = ecrod
Term of locked energy (equivalent to an energy of work hardening) relating to the evolution of
the damage of compression. Allows to control the shape of the peak in compression.
The Young modulus E and the Poisson's ratio
are to be specified by key words ELAS or
ELAS_FO.
In the case of a nonlocal calculation with formulation GRAD_EPSI, the characteristic length is
to specify behind key word NON_LOCAL.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
54/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
5.4
Key word factor NON_LOCAL
This key word factor makes it possible to inform the characteristics necessary to the use of models of
behavior not buildings for which the response of material is not defined any more on a point scale
hardware but with that of the structure, to also see AFFE_MODELE [U4.41.01] and the booklet [R5.04].
5.4.1 Syntax
NON_LOCAL
=
_F
(
LONG_CARA
=
length,
COEF_RIGI_MINI = coeff,
)
5.4.2 Operands
LONG_CARA/COEF_RIGI_MINI
LONG_CARA:
Determine the length characteristic or scale length internal to material.
COEF_RIGI_MINI
With as for him an algorithmic role since it fixes, for the models of damage which degrades
rigidity of material, the proportion of initial rigidity IE of the Young modulus defines under ELAS (0,1%
for example) in on this side which one stops the damage mechanism: this residual rigidity
allows to preserve the character posed well of the elastic problem.
5.5
Key word factor RUPT_FRAG/RUPT_FRAG_FO
The theory of the rupture of Frankfurt and Marigo makes it possible to modelize the appearance and the propagation of
fissures in a fragile springy medium, to see [R7.02.11]. It is based on the criterion of Griffith who
compare the elastic restitution of energy and the energy dissipated during the creation of a surface
fissured, provided by key word GC.
The joined elements use operand GC and operands SIGM_C and SAUT_C within the framework of the law
of behavior BARENBLATT.
5.5.1 Syntax
RUPT_FRAG
=_F
(
GC
=
gc
,
[R]
SIGM_C
=
sigm,
[R]
PENA_ADHERENCE
=
pad, [R]
PENA_CONTACT
=
/
pco, [R]
/1. ,
[DEFECT]
)
RUPT_FRAG_FO
=_F
(
GC
=
gc
,
[function **]
SIGM_C
=
sigm,
[function **]
PENA_ADHERENCE
=
pad, [function **]
PENA_CONTACT
=
pco, [function **]
)
5.5.2 Operand
RUPT_FRAG
Dissipated energy is proportional to the surface of fissure created, the proportionality factor
being the tenacity of the material G
C
.
5.5.3 Operand
SIGM_C
Critical stress in the beginning from which the fissure will open and the stress between the lips
to decrease.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
55/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
5.5.4 Operand
PENA_ADHERENCE
Small parameter of regularization of the stress in zero (for more details to see [R7.02.11]).
Note:
Parameters
SIGM_C
and
PENA_ADHERENCE
are only obligatory in the case of
modeling
PLAN_FISSURE
. They are not used for the criterion of Griffith, this is why
they appear optional on the level of the catalog.
5.5.5 Operand
PENA_CONTACT
Small parameter of regularization.
5.6
Key word factor CORR_ACIER
Law CORR_ACIER is a model of behavior of the steel, subjected to corrosion in
reinforced concrete structures. This model is developed in 1D and elastoplastic 3D endommageable with
isotropic work hardening and is based on the model of Lemaître [R7.01.20].
()
(
)
=
-
=
=
-
=
>
-
-
-
m
eq
p
y
eq
kp
R
D
p
R
D
p
R
D
/
1
1
~
1
2
3
0
1
&
&
&
&
&
In the plastic range
D
= 0, if not
(
)
D
D
R
p
p
p
p
Cd.
D
-
-
=
5.6.1 Syntax
CORR_ACIER = _F
(
D_CORR
=
cd.
,
[R]
ECRO_K
=
K,
[R]
ECRO_M
=
m,
[R]
SY
=
sy,
[R]
)
5.6.2 Operand
D_CORR
Critical coefficient of damage.
5.6.3 Operands
ECRO_K, ECRO_M
Coefficients of the law of work hardening
m
kp
R
/
1
=
.
5.6.4 Operand
SY
Initial elastic limit, noted
y
in the equations.
Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
56/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
6 Behaviors
thermics
The various thermal behaviors are excluded mutually.
6.1
Key words factor
THER
/
THER_FO
Definition of the constant linear thermal characteristics or function defined by a concept of
type
function
parameter
“INST”
.
6.1.1 Syntax
|
/
THER
=
_F
(
RHO_CP
=
CP
,
[R]
LAMBDA
=
,
[R]
)
/
THER_FO
=
_F
(
RHO_CP
= CP
, [fonction+]
LAMBDA
=
, [fonction+]
)
6.1.2 Operands
LAMBDA
/
RHO_CP
LAMBDA =
Isotropic thermal conductivity.
RHO_CP = CP
Voluminal heat with constant pressure (voluminal product bulk and heat
specific). It is the coefficient appearing in the equation:
(
)
CP T
T
F
& div. grad.
-
=
6.2
Key word factor
THER_ORTH
Definition of the thermal characteristics for an orthotropic material.
The reader will be able to refer to following documentations:
[U4.42.03]
DEFI_COQU_MULT
[U4.42.01]
AFFE_CARA_ELEM
to define the longitudinal direction associated with the hulls or the nonisotropic 3D.
NR
T
L
L, T: directions of orthotropism
longitudinal and transverse
6.2.1 Syntax
/
THER_ORTH
=
_F
(
RHO_CP =
CP, [R]
LAMBDA_L
= lal
, [R]
LAMBDA_T
= lat
, [R]
LAMBDA_N
= lan
, [R]
)

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
57/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
6.2.2 Operands
LAMBDA/RHO_CP
LAMBDA_L = lal
Thermal conductivity in the longitudinal direction.
LAMBDA_T = lat
Thermal conductivity in the transverse direction.
LAMBDA_N = lan
Thermal conductivity in the normal direction.
RHO_CP = CP
Voluminal heat.
6.3
Key word factor
THER_NL
(cf [R5.02.02])
Allows to describe the thermal characteristics depending on the temperature. The formulation made
to intervene voluminal enthalpy.
(
)
.
div () grad
.
-
=
T
T
F
6.3.1 Syntax
/
THER_NL
=
_F
(
/BETA =
, [function **]
/
RHO_CP
=
CP
,
[function **]
LAMBDA
=
, [function **]
)
6.3.2 Operands
BETA
/
LAMBDA
/RHO_CP
/BETA
=
Voluminal enthalpy function of the temperature. For the enthalpy, the prolongations of
function are necessarily linear.
/RHO_CP = CP
Voluminal heat.
LAMBDA
=
Thermal conductivity isotropic function of the temperature.
6.4
Key words factor
THER_COQUE/THER_COQUE_FO
Allows to define membrane and transverse conductivities and the heat capacity for
homogenized heterogeneous thermal hulls.
Directions 1 and 2 indicate those of the plan of the plate, direction 3 is perpendicular. One
admits that the tensor of conductivity in each point is diagonal and that its eigenvalues are l1,
l2 and l3. The coefficients are thus defined by the user in the reference mark of orthotropism of the plate.
The code makes then the change of reference mark to find the correct values in the reference mark of
the element.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
58/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
6.4.1 Syntax
/
THER_COQUE/THER_COQUE_FO
=
_F (
COND_LMM = a1111,
[R]
or
[fonction+]
COND_TMM = a2211,
[R]
or
[fonction+]
COND_LMP = a1111,
[R]
or
[fonction+]
COND_TMP = a2211,
[R]
or
[fonction+]
COND_LPP = a1111,
[R]
or
[fonction+]
COND_TPP = a2211,
[R]
or
[fonction+]
COND_LSI = a1111,
[R]
or
[fonction+]
COND_TSI = a2211,
[R]
or
[fonction+]
COND_NMM = b11
,
[R] or [fonction+]
COND_NMP = b12
,
[R] or [fonction+]
COND_NPP = b22
,
[R] or [fonction+]
COND_NSI = b23
,
[R] or [fonction+]
CMAS_MM = c11
,
[R] or [fonction+]
CMAS_MP = c12
,
[R] or [fonction+]
CMAS_PP = c22
,
[R] or [fonction+]
CMAS_SI = c23
,
[R] or [fonction+]
)
6.4.2 Operands
COND_LMM/COND_LMP/COND_LPP/COND_LSI/COND_TMM/
COND_TMP/COND_TPP/COND_TSI
P1, P2, P3 indicate the functions of interpolation of the temperature in the thickness.
If A is the matrix of surface average conductivity defined in the note [R3.11.01], one has then for
the membrane tensor of conductivity.
COND_LMM = a1111
term related to the integral of l1 * P1 * P1
COND_LMP = a1112
term related to the integral of l1 * P1 * P2
COND_LPP = a1122
term related to the integral of l1 * P2 * P2
COND_LSI = a1123
term related to the integral of l1 * P2 * P3
COND_TMM = a2211
term related to the integral of l2 * P1 * P1
COND_TMP = a2212
term related to the integral of l2 * P1 * P2
COND_TPP = a2222
term related to the integral of l2 * P2 * P2
COND_TSI = a2223
term related to the integral of l2 * P2 * P3

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
59/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
6.4.3 Operands
COND_NMM/COND_NMP/COND_NPP/COND_NSI
If B is the tensor which describes transverse conduction and the exchanges on surfaces omega+ and
Omega, defined in the note [R3.11.01], one has for the transverse tensor of conductivity:
COND_NMM = b11
term related to the integral of l3 * P1 * P1
COND_NMP = b12
term related to the integral of l3 * P1 * P2
COND_NPP = b22
term related to the integral of l3 * P2 * P2
COND_NSI = b23
term related to the integral of l3 * P2 * P3
6.4.4 Operands
CMAS_MM/CMAS_MP/CMAS_PP/CMAS_SI
One has finally for the tensor of heat capacity.
CMAS_MM = c11
term related to the integral of RHOCP * P1 * P1
CMAS_MP = c12
term related to the integral of RHOCP * P1 * P2
CMAS_PP = c22
term related to the integral of RHOCP * P2 * P2
CMAS_SI = c23
term related to the integral of RHOCP * P2 * P3

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
60/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
7
Behaviors specific to the concretes
7.1
Key word factor THER_HYDR
Allows to define the behavior associated with the hydration with the concrete.
The hydration of the concrete is a phenomenon which is accompanied by a release of heat depending
temperature [R7.01.12].
()
-
=
+
=
+
T
grad
S
dt
T
D
Q
div
dt
D
Q
Q
éq
7.1-1
()
-
=
RT
E
With
dt
D
has
exp
éq 7.1-2
7.1.1 Syntax
THER_HYDR =_F (
LAMBDA
=
lambda
,
[function **]
BETA =
beta,
[function **]
AFFINITY
=
With
,
[function]
CHALHYDR
=
Q
,
[R]
QSR_K
=
QsR
,
[R]
)
7.1.2 Operands
LAMBDA/BETA
LAMBDA = lambda
Thermal conductivity isotropic function of the temperature.
BETA = beta
Voluminal enthalpy function of the temperature. The prolongations are has minimum linear,
voluminal enthalpy being able to be defined as the integral of voluminal heat.
7.1.3 Operand
AFFINITY
AFFINITY = A
Function of the degree of hydration determined by a calorimetric test of the concrete (function of
size HYDR).
7.1.4 Operand
CHAL_HYDR
CHAL_HYDR = Q
Heat released per unit of hydration (presumedly constant), this function depends on the type on
concrete.
7.1.5 Operand
QSR_K
QSR_K
Constant of Arrhenius expressed in Kelvin degree.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
61/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
7.2
Key word factor
SECH_GRANGER
Definition of the parameters characterizing the coefficient of dissemination
(
)
D C T
,
intervening in the equation
nonlinear of drying proposed by Granger (cf [R7.01.12]). These characteristics are
constants, while the coefficient of dissemination depends on the variable of calculation, i.e.
concentration
C
current out of water, (as thermal conductivity depended on the temperature).
7.2.1 Syntax
SECH_GRANGER
=_F
(
With = has, [R]
B = B, [R]
QSR_K = QsR
,
[R]
TEMP_0_C = t0
, [R]
)
7.2.2 Operands
With
/
B
/
QSR_K
/
TEMP_0_C
These coefficients make it possible most usually to express the coefficient of dissemination in its form
used in the literature and suggested by L. Granger:
D C T
E has
T
T E
B C
Q
R T T
S
(,)
.
(. )
=
-
-
0
1 1
0
A=
has
Varying coefficient of dissemination of 0.5 10
13
and 2.10
13
m
2
/S for the concrete.
B=
B
Coefficient of about 0.05 for the concrete.
QSR_K=
QsR
QsR is worth 4700 in general. K. (R is the constant of perfect gases).
TEMP_0_C=
T0
Temperature of reference in the law of Arrhenius. The temperature of T0 reference is in degrees
Centigrade, and converted into Kelvin at the time of the resolution.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
62/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
7.3
Key word factor
SECH_MENSI
Definition of the parameters characterizing the coefficient of dissemination intervening in the equation not
linear of drying proposed by Mensi (cf [R7.01.12]). These characteristics are constants,
while the coefficient of dissemination depends on the variable of calculation, i.e. concentration
C
current out of water, (as thermal conductivity depended on the temperature). It is one
formulation simplified of the general case, constituting the law of Mensi.
7.3.1 Syntax
SECH_MENSI
=
_F
(
With
=
has, [R]
B
=
B, [R]
)
7.3.2 Operands
With
/
B
These coefficients make it possible to express the coefficient of dissemination according to the law of Mensi:
)
.
(
.
)
(
C
B
E
has
C
D
=
A=
has
Varying coefficient of dissemination of 0.5 .10
13
and 2.10
13
m
2
/S for the concrete.
B=
B
Coefficient of about 0.05 for the concrete.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
63/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
7.4
Key word factor
SECH_BAZANT
Definition of the parameters characterizing the coefficient of dissemination intervening in the equation not
linear of drying proposed by Bazant (cf [R7.01.12]). These characteristics are constants,
while the coefficient of dissemination depends on the variable on calculation, i.e. the concentration
C
current out of water, (as thermal conductivity depended on the temperature). This formulation
constitute the law of Bazant.
7.4.1 Syntax
SECH_BAZANT
=
_F
(
D1 =
d1,
ALPHA_BAZANT
=
,
[R]
NR =
N,
[R]
FONC_DESORP =
desorp,
[function **]
)
7.4.2 Operands
D1
/
ALPHA_BAZANT
/
NR
/FONC_DESORP
These coefficients make it possible to express the coefficient of dissemination according to the law of Bazant:
D H
D
H
N
()
.
=
+
-
+
-
-
1
1
1
1
1 0 75
where
H
is the degree of hydration, related to the water concentration by the curve of desorption.
D1=
d1
Coefficient of dissemination which is about 3.10
13
m
2
/S for the concrete.
ALPHA_BAZANT=
Varying coefficient from 0.025 to 0.1 for the concrete.
N=
N
Exposing about 6 for the concrete.
FONC_DESORP=
desorp
Curve of desorption, allowing to pass from the water concentration to the degree of hydration h.
Important remark:
desorp
is a function of the variable of calculation, C, the water concentration, which is comparable
for the resolution at a temperature, of type
“TEMP”
.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
64/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
7.5
Key word factor
SECH_NAPPE
The coefficient of dissemination, characterizing the nonlinear equation of drying, is expressed using one
tablecloth, tabulée function of the water concentration, variable of calculation, and the temperature, variable
auxiliary of calculation, given in the form of a structure of data of the type
evol_ther
. For
resolution of drying by the operator
THER_NON_LINE
, the water concentration is comparable with one
temperature, of type
“TEMP”
.
For the coherence of the data, parameters of the tablecloth, i.e. the variable of calculation and
auxiliary variable cannot be of the same type. A new type of variable was added in
DEFI_NAPPE
, the “type of the temperature calculated drying before”,
“TSEC”
, which
corresponds indeed to a temperature.
7.5.1 Syntax
SECH_NAPPE
=
_F
(
FUNCTION
= nom_fonc, [function]
)
7.5.2 Operand
FUNCTION
The coefficient of dissemination is expressed using a tabulée function of the parameters
C
and
T
.
FUNCTION = nom_fonc
Name of the tablecloth.
7.6
Key word factor
PINTO_MENEGOTTO
Definitions of the coefficients of the relation of cyclic behavior of elastoplasticity of the reinforcements in
steel in the concrete reinforced according to the model with Pinto-Menegotto (cf [R5.03.09]).
The initial traction diagram (beginning of the loading) is defined by:
·
=
E
y
as long as
;
E
defined under ELAS
·
=
y
y
H
E
for
·
(
)
=
-
-
-
-
<
U
U
y
U
U
H
H
U
4
for
(
cannot exceed
U
)
The curve
()
= F
in the nth cycle is defined by:
(
)
ue
asymptotiq
E
écrouissag
of
slope
and
with
:
)
(
1
1
2
1
0
*
1
*
*
*
H
H
L
R
R
L
L
L
E
E
E
B
has
has
R
R
B
B
=
+
-
=
+
-
+
=
where
*
is defined by:
*
=
-
-
-
-
RN
yn
RN
1
1
.
where
*
is defined by:
1
1
*
N
y
N
y
N
R
-
-
=
-
.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
65/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
Quantity
yn
is deduced from the cycle
N
- 1
by:
(
)
(
)
yn
RN
yn
RN
yn
yn
yn
RN
H
RN
yn
E
sign
E
=
+
-
=
-
+
-
-
-
-
-
-
-
-
1
1
1
1
1
1
1
.
The variable
is defined by:
=
-
-
-
-
-
RN
yn
yn
RN
1
1
1
where
RN-1
represent the deformation reached at the end of
N
- 1
ème semi-cycle
and
yn
yn
- 1
,
the deformations of end of linearity of the semi-cycles represent
N
N
- 1
and
.
B
represent either the value provided by the user (key word EP_SUR_E) or, failing this:
B
E
E
with
E
E
H
H
U
y
U
y
=
=
-
-
In the event of buckling, (if
L D
/
> 5
):
·
in compression one replaces
B
by
B
has
L D E
C
B
E
y
=
-
-
(.
/)
5 0
·
in traction, one calculates a new slope
(
)
(
)
E
E has
E has
R
has
RN
y
N
=
+
-
-
-
-
-
5
5
10
6
1
1
(.
)
with
has
L D
5
1 5 75
= + -.
.
represent the greatest “plastic excursion” during the loading:
(
)
=
-
max
N
RN
yn
and
= 4
y
L D
In the case of buckling, one adds to
yn
the value
S
S
C
C
Be B B
B
*
=
-
-
1
with
S
Cl
D
L D
E
=
-
-
11
10
1
.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
66/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
7.6.1 Syntax
|
PINTO_MENEGOTTO = _F
(
SY
=
sigm,
[R]
EPSI_ULTM
= epsu, [R]
SIGM_ULTM
= sigmu, [R]
DASH =/L/D
,
[R]
/
4.
,
[DEFECT]
EPSP_HARD
= epsh, [R]
R_PM =/R0
, [R]
/
20.
,
[DEFECT]
EP_SUR_E = B, [R]
A1_PM
=/
a1
, [R]
/
18.5,
[DEFECT]
A2_PM
=/
a2
, [R]
/
0.15,
[DEFECT]
A6_PM
=/
a6
, [R]
/
620. ,
[DEFECT]
C_PM =/
C, [R]
/
0.5
,
[DEFECT]
A_PM =/
has, [R]
/
0.006
,
[DEFECT]
)
7.6.2 Operands
SY = sigm
Initial elastic limit, noted
y
in the equations.
EPSI_ULTM =
epsu,
noted
U
in the equations.
Ultimate deformation.
SIGM_ULTM = sigmu
,
noted
U
in the equations.
Ultimate stress.
DASH = L/D
Twinge of the bar (>5: buckling).
EPSP_HARD = epsh
,
noted
H
in the equations.
Deformation corresponding at the end of the plastic bearing.
EP_SUR_E = B
Ratio slope of work hardening/Young modulus (if no value is given, one takes
B
E
E
H
=
).

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
67/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
A1_PM = a1
Coefficient defining the traction diagram of the model.
A2_PM = a2
Coefficient defining the traction diagram of the model.
A6_PM = a6
Coefficient defining the traction diagram of the model in the event of buckling.
C_PM = C
used in
S
Coefficient defining the traction diagram of the model in the event of buckling.
A_PM = has
Coefficient defining the traction diagram of the model in the event of buckling.
R_PM =
Coefficient R
O
(20. By defect).
The Young modulus
E
and the thermal expansion factor
ALPHA
are to be specified by the key words
ELAS
or
ELAS_FO
.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
68/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
7.7
Key words factor BPEL_BETON/BPEL_ACIER
Definition of the characteristics intervening in the model of behavior of the cables of
prestressed [R7.01.02].
The linear elastic characteristics of the material concrete and the material steel must be
at the same time definite under key word ELAS.
7.7.1 Syntax
/
BPEL_BETON =
_F (
PERT_FLUA
=/xflu, [R]
/
0.
,
[DEFECT]
PERT_RETR
=/xret, [R]
/
0.
,
[DEFECT]
)
/
BPEL_ACIER =
_F (
RELAX_1000 =/rh1000
, [R]
/
0.
,
[DEFECT]
MU0_RELAX
=
/
mu0
,
[R]
/
0.
,
[DEFECT]
F_PRG
=
fprg,
[R]
FROT_COURB =/F, [R]
/
0.
,
[DEFECT]
FROT_LINE
=
/
phi
,
[R]
/
0.
,
[DEFECT]
)
)
7.7.2 Operands
Behavior: BPEL_BETON
Key word factor for the definition of the parameters characteristic of the material concrete which
intervene in the estimate of the losses of voltage along the cables of prestressing. It
key word factor can be used only jointly with the key word factor
ELAS
.
PERT_FLUA = xflu
Standard rate of loss of voltage by creep of the concrete, compared to the initial voltage.
flu
flu
F
X
F
=
.
0
where
0
F
indicate the initial voltage defines by DEFI_CABL_BP.
The default value is 0: in this case, one does not take account of the losses of voltage by
creep of the concrete.
PERT_RETR = xret
Standard rate of loss of voltage by shrinking of the concrete, compared to the initial voltage.
ret
ret
F
X
F
=
.
0
where
0
F
indicate the initial voltage.
The default value is 0: in this case, one does not take account of the losses of voltage by
shrinking of the concrete.
Behavior: BPEL_ACIER
Key word factor for the definition of the parameters characteristic of the material steel which
intervene in the estimate of the losses of voltage along the cables of prestressing. This word
key factor can be used only jointly with the key word factor
ELAS
.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
69/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
RELAX_1000 = rh1000
Relieving of steel at 1000 hours, expressed in %.
The default value is 0: in this case, one does not take account of the losses of voltage by
relieving of steel.
MU0_RELAX = mu0
Adimensional coefficient of relieving of prestressed steel.
The default value is 0.
F_PRG = fprg
Guaranteed stress of the maximum loading with rupture (according to the BEPL).
If one takes account of the losses of voltage by relieving of steel (
RELAX_1000
informed
by a nonnull value), it is obligatorily necessary to inform operand F_PRG, by a value
nonnull.
FROT_COURB = F
Coefficient of friction of the cable on the partly curved concrete, in rad
1
. The default value
is 0.
FROT_LINE = phi
Coefficient of friction per unit of length, partly right. The default value is 0.
7.8
Key word factor
CONCRETE
_
DOUBLE_DP
The model of behavior 3D developed in Code_Aster is formulated within the framework of
thermo plasticity, for the description of the nonlinear behavior of the concrete, in traction, and in
compression, with the taking into account of the irreversible variations of the thermal characteristics and
mechanics of the concrete, particularly sensitive at high temperature [R7.01.03].
7.8.1 Syntax
| /BETON_DOUBLE_DP=
_F
(
F_C= f' C,
[function *]
F_T= f' T,
[function *]
COEF_BIAX=
,
[function *]
ENER_COMP_RUPT=
Gc
,
[function *]
ENER_TRAC_RUPT= WP
,
[function *]
COEF_ELAS_COMP=
,
[function *]
LONG_CARA =
will l_cara,
ECRO_COMP_P_PIC=
/“LINEAR”, [DEFECT]
/“PARABOLA”, [TXM]
ECRO_TRAC_P_PIC=
/“LINEAR”, [DEFECT]
/“EXPONENT”, [TXM]
)
BETON_DOUBLE_DP
allows to define all the characteristics associated with the law with behavior
with double criterion of Drücker Prager. In complement of these characteristics, the modulus of elasticity,
the Poisson's ratio, and the thermal expansion factor
, as well as the coefficients of withdrawal
endogenous and of withdrawal of desiccation, must be defined under the key word
ELAS
for the coefficients
realities, or
ELAS_FO
, for the coefficients defined by functions, or tablecloths. All them
characteristics of the model, (E, naked,
, f' C, f' T, Gc, Gt) of type [function *] can depend on one
or of two variables among the temperature, the hydration and drying. When they depend on
temperature, they are functions of the maximum of the temperature reached during the history of
loading
, which is stored for each point of Gauss, in the form of variable
intern. This makes it possible to take into account the irreversible variations of these characteristics to high
temperature.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
70/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
7.8.2 Operands
F_C/
F_T/
COEF_BIAX
F_C=
f' C
Resistance in uniaxial pressing f'
C
.
F_T= f' T
Resistance in uniaxial traction f'
T
.
COEF_BIAX=
The report/ratio of resistance in biaxial compression to resistance in uniaxial pressing
.
7.8.3 Operands
ENER_COMP_RUPT/
ENER_TRAC_RUPT/COEF_ELAS_COMP
ENER_COMP_RUPT=
Gc
The energy of rupture in compression G
C
,
ENER_TRAC_RUPT= WP
The energy of rupture in traction G
T
.
COEF_ELAS_COMP=
Elastic limit in compression, given by a proportionality factor expressed as a percentage
resistance to the peak F
C
'(
), in general, about 30% for the standard concretes.
7.8.4 Operands
LONG_CARA
This operand makes it possible to overload the automatically calculated characteristic length, for
each mesh, according to its dimensions (starting from its surface in 2D, its volume in
3D).
The automatically calculated characteristic length allows, when the smoothness of the mesh evolves/moves
from one calculation to another, to preserve stable results by avoiding the phenomena of localization.
This length calculated automatically or given by the user, conduit with the value of
ultimate work hardening in traction according to the formula (for a linear work hardening post-peak):
()
()
()
=
T
C
T
U
F
L
G
.
.
2
In the particular case of a mesh containing of the adjacent meshs whose dimensions are very
different, ultimate work hardenings of the model
BETON_DOUBLE_DP
calculated starting from the length
characteristic of the meshs are consequently very different, which can generate problems
of convergence or to lead to a not very physical state of stresses. (This characteristic length is
calculated starting from the volume of the current mesh). For this reason, one proposes to give
possibility with the user of defining an average length which overloads the characteristic length
calculated for each mesh. The defect of Code_Aster is the characteristic length calculated for
each mesh.
To choose an arbitrary and identical length for all the meshs can also generate difficulties
of convergence. The best solution consists in creating a network of which variations of dimensions
meshs respect the direction of variation of the stress field, and to use the length
characteristic calculated automatically according to the size of the meshs. The overload by
LONG_CARA
must be to reserve for particular cases, when the user cannot freely intervene
on the mesh.
If the user defines the characteristic length in material, it will choose a couple (
T
G
,
LONG_CARA) such as
()
()
T
C
T
F
L
G
.
.
2
the value is worth which it wishes for ultimate work hardening in traction
U
.
(The usual value of the deformation associated with ultimate work hardening in traction with an average concrete is
of 5.E-4).

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
71/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
7.8.5 Operands
COMP_POST_PIC/TRAC_POST_PIC
The parameters making it possible to define the curve of softening in compression and traction are
optional, and have default values.
ECRO_COMP_P_PIC=
/“LINEAR”
/
“PARABOLA”
Form curve post-peak in compression of the text type, which can take the values
“LINEAR”
and
“PARABOLA”
. The nonlinear curve is then of parabolic type.
ECRO_TRAC_P_PIC=
/“LINEAR”
/
“EXPONENT”
Form curve post-peak in traction of the text type, which can take the values
“LINEAR”
and
“EXPONENT”
. The nonlinear curve is then of exponential type.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
72/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
7.9
Key word factor GRANGER_FP/GRANGER_FP_INDT/V_GRANGER_FP
Definition of the parameters materials for the viscoelastic model of Granger, modelizing creep
clean of the concrete. There are 3 relations of behavior: the first GRANGER_FP does not take in
count the phenomenon of ageing, the second GRANGER_FP_INDT is identical without effect of
the temperature, the third V_GRANGER_FP accounts for ageing. Cf [R7.01.01].
In 1D and creep the model is written:
fl
T
J T Tc T H
()
(,)
=
0
with
J T T T H
H T
Tref
K Tc
J
T
T
C
eq
S
eq
C
S
S
N
(,)
(
)
(
)
(
exp
)
= -
-
-
-
-
=
45
45
1
1
C
T
indicate the time of loading
()
C
C
H
1
-
=
, or
C
is the isothermal curve of desorption
T
T
U
R T S
ds
eq
C
S T
T
()
exp
()
=
-
-
=
1
1
293
0
K Tc
Tc
eq
eq
(
)
.
.
.
=
+
+
28
01
1
0 2
0 2
if one takes into account the phenomenon of ageing,
()
1
=
eq
Tc
K
if not
Tc
T
U
R T S
T
ds
eq
C
ref.
S T
T
C
()
exp
()
v
=
-
-
=
1
1
0
Note:
ref.
T
is the temperature of reference, it is chosen by the user using the control
AFFE_MATERIAU.
This behavior can be associated the effects of dilation and thermal withdrawal defined by
operands K_DESSIC and B_ENDOGE under key word ELAS_FO.
For GRANGER_FP_INDT, the temperature does not intervene. Thus the multiplicative term
45
)
45
(
-
- Tref
T
is removed, just as the dependence of
)
(T
T
eq
at the temperature.
7.9.1 Syntax for clean creep
|
GRANGER_FP = _F (
J1
=
J1
,
[R]
J2
=
J2
,
[R]
J3
=
J3
,
[R]
J4
=
J4
,
[R]
J5
=
J5
,
[R]
J6
=
J6
,
[R]
J7
=
J7
,
[R]
J6
=
J8
,
[R]
TAUX_1
=
1
,
[R]
TAUX_2
=
2
,
[R]
TAUX_3
=
3
,
[R]
TAUX_4
=
4
,
[R]
TAUX_5
=
5
,
[R]
TAUX_6
=
6
,
[R]
TAUX_7
=
7
,
[R]
TAUX_8
=
8
,
[R]

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
73/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
QSR_K
=
qsr
,
[R]
)
7.9.2 Operands for clean creep
J1 =
J1
…
…
.J8 =
J8
8 coefficients materials of the function of creep, homogeneous at a time.
TAUX_1
=
1
…
…
.TAUX_8 =
8
8 coefficients of “delay” of the function of creep, homogeneous at a time.
QSR_K
= CPU/R
Constant energy of activation intervening in the time term are equivalent teq modelizing the effect of
temperature on the kinetics of creep.
7.9.3 Syntax for clean creep independent of the temperature
Syntax is identical to the case with effect of the temperature, without key word QSR_K.
7.9.4 Syntax for ageing
If one uses the relation of behavior which then takes into account the phenomenon of ageing it
is necessary to inform moreover:
V_GRANGER_FP =_F (
QSR_VEIL
=
USR
,
[R]
FONC_V
=
K (tceq)
, [function,
formulate]
)
7.9.5 Operands for ageing
QSR_VEIL = USR
Constant energy of activation intervening in the time term of load are equivalent tceq modelizing
the effect of the temperature on ageing
U
R
C
.
FONC_V = K (tceq)
Function of ageing
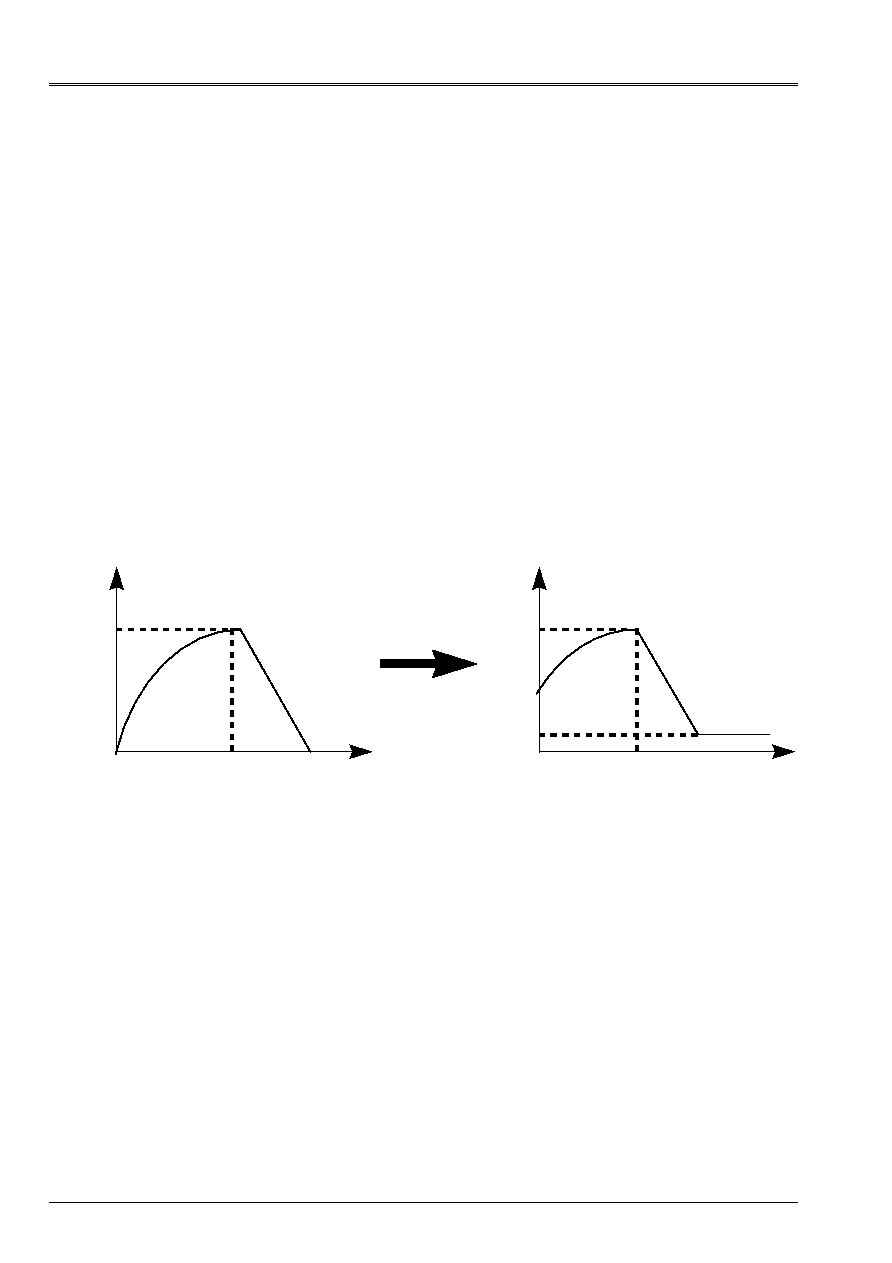
Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
74/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
7.10 Word
key
NADAI_B
The law of behavior NADAI_B is a model of behavior of the integral concrete of
plastic deformations in compression and a model of cracking in traction. This model allows
to represent the behavior of the concrete under cyclic loading, a detailed attention being
brought to the management of the openings and closings of the fissures.
For behavior in compression, modeling is developed within the framework of
standard elastoplasticity: threshold of reversibility (standard Drücker-Prager), normal plastic flow
associated.
For behavior in traction, the model is within the framework of cracking distributed. A threshold
of reversibility in traction is defined. The first cracking is detected in a geometrical point
given when the stresses exceed the threshold in traction for the first time. The point is then
declared fissured, direction of the fissure being direction perpendicular to the main stress
major at this moment. The law of behavior of the concrete in this point becomes an orthotropic law then, them
axes of orthotropism being those parallel and perpendicular to the fissure (of which the orientation of will change
more)
The parameters of the law are given starting from a test in uniaxial pressing, resistance
in traction of the concrete:
F
T
and of the deformation with rupture in traction:
rupture
tration
Stress-strain curve in compression, one deduces the stress-strain curve
plastic in compression.
Test of uniaxial pressing
Plastic stress-strain curve
rupture
peak
F
it
F
it
0 05
, F
it
F
it
K
peak
K
rupture
Curve stress-strain curve plastic in compression, one deduces:
F
C
:
stress ultimate in compression
:
parameter such as
F
C
the surface of initial load in compression defines
K
peak
:
plastic deformation with the peak
K
rupture
:
plastic deformation with rupture
The user who would not have the tests necessary to provide these data can use them
payments which make it possible to estimate a value of the Young modulus, Poisson's ratio,
limit in traction according to the stress ultimate in compression. For the user who would not like
not to do this work, we recommend values
F,
,
you
K
K
peak
rupture
rupture
traction
,
and the factor
of shearing tranverse which is practically inaccessible to the measurement.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
75/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
7.10.1 Syntax
We indicate Ci below the correspondence between the key words of behavior NADAI_B and them
preset parameters Ci above:
|
/NABAI_B
:
_F
(
F_C
:
FC
F_T
:
ft
CRIT_E_C: theta
EPS_P_C: epc
EPS_R_C: erc
EPSI_R_T: ert
FAC_T_C: F
)
The Young modulus E
0
and the Poisson's ratio
are those provided under the key word factor
ELAS
.
7.10.2 Operands F_C/F_T
F_C
:
FC stress ultimate in compression
F_T
:
ft stress ultimate in traction value recommended 0,1
C
F
7.10.3 Operand CRIT_E_C
CRIT_E_C:
theta: parameter allowing to define the surface of initial load in
compression. Value recommended 0,3
7.10.4 Operands EPS_P_C/EPS_R_C/EPSI_R_T
EPS_P_C:
epc: plastic deformation or peak
EPS_R_C:
erc: plastic deformation with rupture. Value recommended 0,0005
EPSI_R_T:
ert: deformation with rupture in traction. Value recommended 0,0005
7.10.5 Operand FAC_T_C
FAC_T_C:
F: factor of transfer of shearing. Value recommended 0,4
7.11 Key word factor BAZANT_FD
Model BAZANT_FD is a viscoelastic model of intrinsic creep of desiccation according to
model of Bazant. It is a long-term behavior of the concretes subjected to drying and one
mechanical loading simultaneously. The document [R7.01.05] described the corresponding details.
Note:
It is necessary to inform key word FONC_DESORP under behavior ELAS_FO.
This behavior can be associated the effects of dilation and thermal withdrawal defined by
operands K_DESSIC and B_ENDOGE under key word ELAS_FO.
7.11.1 Syntax
BAZANT_FD = _F
(
LAM_VISC =
,
[R]
)
7.11.2 Operand
LAM_VISC
= parameter material in
[]
1
-
AP
.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
76/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
7.12 Word
key
LABORD_1D
This model of nonlinear behavior of the concrete is employed in uniaxial situations under
the effect of monotonous and cyclic loadings. The model is described within the framework of formulation
thermodynamics of the irreversible processes. It makes it possible to take account of the damage of
concrete in traction and compression, separately, manages the opening and refermeture of the fissures, and
account of the nonreversible deformation takes.
This model was developed to be employed with the multifibre elements of beam [R7.01.07].
Note:
The taking into account of the effect of a thermal loading is not possible for the moment.
7.12.1 Syntax
/
LABORD_1D
= _F
(
Y01
=
Y01
,
[R]
Y02
=
Y02
,
[R]
A1
=
A1
,
[R]
A2
=
A2
,
[R]
B1
=
B1
,
[R]
B2
=
B2
,
[R]
BETA1
=
1
,
[R]
BETA2
=
2
,
[R]
SIGF =
F
,
[R]
);
7.12.2 Operands
Y01
=
Y01
Threshold of evolution of the variable of damage under traction
Y02
=
Y02
Threshold of evolution of the variable of damage under compression
A1 = A1
Parameter
describing multiplier
kinetics
of evolution
of
variable
of damage
under traction
A2 = A2
Parameter
describing multiplier
kinetics
of evolution
of
the variable
of damage
under compression
B1 = B1
Parameter
of
power
describing the kinetics
of evolution
of
variable
of damage
under traction
B2 = B2
Parameter of
power
describing
kinetics
of evolution
of
the variable
of damage
under compression
BETA1 = 1
Parameter describing the amplitude of the anelastic deformation under traction
BETA2 = 2
Parameter describing the amplitude of the anelastic deformation under compression
SIGF = F
Parameter indicating the stress of opening and refermeture of fissure

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
77/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
7.13 Key word factor MAZARS/MAZARS_FO
The model of behavior of Mazars is an elastic model of behavior endommageable
allowing to describe the softening behavior of the concrete. It distinguishes behavior in traction
and in compression, but uses only one variable of scalar damage (cf [R7.01.08]).
The parameters can be a function of the temperature, to use MAZARS_FO then. Attention, in
practical, it is considered that the parameters depend on the maximum temperature seen by material.
7.13.1 Syntax
|
/MAZARS
=
_F (
EPSD0 = d0, [R]
AC
=
Ac
,
[R]
AT
=
At
,
[R]
BC
=
Bc
,
[R]
BT
=
LT
,
[R]
BETA =, [R]
)
/
MAZARS
=
_F (
EPSD0 = d0, [function **]
AC
=
Ac
,
[function **]
AT
=
At
,
[function **]
BC
=
Bc
,
[function **]
BT
=
LT
,
[function **]
BETA =, [R]
)
MAZARS (or MAZARS_FO) makes it possible to define all the characteristics associated with the model with
behavior of Mazars. In addition to these characteristics, constant the rubber bands must be
defined under key word ELAS for the real coefficients or ELAS_FO for the coefficients depending
temperature.
7.13.2 Operands EPSD0
EPSD0 =
d0
Threshold of damage in deformation (generally 0.5 10
4
<
d0 < 1.5 10
4
).
7.13.3 Operands AC/AT/BC/BT
AC = ac
Coefficient allowing to fix the shape of the curve post-peak in compression. Introduced one
horizontal asymptote which is the axis of
for ac = 1 and the horizontal one for passer by by the peak for
Ac = 0 (generally 1 < ac < 1.5).
AT = At
Coefficient allowing to fix the shape of the curve post-peak in traction. Introduced an asymptote
horizontal which is the axis of
for ac = 1 and the horizontal one passing by the peak for ac = 0
(generally 0.7 < At < 1).

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
78/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
BC = Bc
Coefficient allowing to fix the shape of the curve post-peak in compression. According to its value can
to correspond to a brutal fall of the stress (BC < 10
4
) or a preliminary phase
of increase in stress followed by a more or less fast decrease (generally
10
3
< Bc < 2 10
3
).
BT = LT
Coefficient allowing to fix the shape of the curve post-peak in traction. According to its value can
to correspond to a brutal fall of the stress (BC < 10
4
) or a preliminary phase
of increase in stress followed by a more or less fast decrease (generally
10
4
< LT < 10
5
).
7.13.4 Operand BETA
BETA =
Parameter of correction for shearing. Value advised 1.06.
7.14 Word
key
BETON_UMLV_FP
The law of creep UMLV supposes a total decoupling between the spherical components and
deviatoric: the deformations induced by the spherical stresses are purely spherical and
the deformations induced by the deviatoric stresses are purely deviatoric. In addition,
clean deformation of creep is supposed to be proportional to internal relative moisture:
Spherical part:
()
S
S
F
H
=
and, left deviatoric:
()
~
F
H
D
=
Where H indicates internal relative moisture.
The model of behavior BETON_UMLV_FP is a nongrowing old viscoelastic model
developed in partnership with the University of marl-the-Valley to describe the clean creep of
concretes. It is particularly adapted to the multiaxial configurations by not presupposing the value
Poisson's ratio of creep.
The spherical stresses are at the origin of the migration of the water absorptive with the interfaces between
hydrates on the level of the macroporosity and absorptive within microporosity in porosity
thin cable. Dissemination of the inter-lamellate water of the pores of hydrates towards capillary porosity
be carried out in an irreversible way. The total spherical deformation of creep is thus written like
summon of a reversible part and an irreversible part:
{
{
irréversib
part
fs
I
reversible
part
fs
R
fs
+
=
The process of deformation spherical of creep is controlled by the system of coupled equations
according to:
[
]
(
)
[
]
[
]
-
-
+
-
=
-
-
=
+
fs
R
Sr
S
fs
I
S
I
Sr
fs
Sr
if
fs
I
fs
I
fs
R
Sr
S
Sr
fs
K
H
K
K
K
K
H
1
1
&
&
&
where
Sr
K
indicate rigidity connect associated with the skeleton formed by blocks with hydrates on the scale
mesoscopic;
Sr
viscosity connects associated with the mechanism with dissemination within porosity
thin cable;
S
I
K
indicate rigidity connect intrinsically associated with the hydrates on the scale
microscopic and
S
I
viscosity connects associated with the interfoliaceous mechanism of dissemination.
(Hooks
+
appoint the operator of Mac Cauley:
(
)
X
X
X
+
=
+
2
1
)
The deviatoric stresses are at the origin of a mechanism of slip (or mechanism of quasi
dislocation) of the layers of HSC in nano-porosity. Under deviatoric stress, creep
be carried out with constant volume. In addition, the law of creep UMLV supposes the isotropy of creep

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
79/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
deviatoric. Phénoménologiquement, the mechanism of slip comprises a contribution
reversible viscoelastic of the water strongly adsorbed with the layers of HSC and a contribution
irreversible viscous of interstitial water:
{
{
{
free
water
one
contributi
fd
I
absobée
water
one
contributi
fd
R
total
ue
déviatoriq N
déformatio
fd
+
=
The J
ème
main component of the total deviatoric deformation is governed by the system
equations following:
J
D
D
R
J
D
D
R
J
D
I
D
R
D
I
D
R
J
K
K
,
,
~
1
~
&
&&
&
+
=
+
+
where
D
R
K
indicate rigidity associated with the capacity with water adsorbed to transmit loads (load
bearing toilets);
D
R
viscosity associated with the water adsorbed by the layers with hydrates and
D
I
indicate
viscosity associated with interstitial water.
7.14.1 Syntax
|
BETON_UMLV_FP
:
_F
(
K_RS:
K_RS
,
[R]
K_IS:
K_IS
,
[R]
K_RD:
K_RD
,
[R]
ETA_RS
:
ETA_RS
,
[R]
ETA_IS
:
ETA_IS
,
[R]
ETA_RD
:
ETA_RD
,
[R]
ETA_ID
:
ETA_ID
,
[R]
)
7.14.2 Operand
K_RS: K_RS
S
R
K
rigidity connects associated with the skeleton formed by blocks with hydrates on the scale
mesoscopic
K_IS: K_IS
S
I
K
rigidity connects intrinsically associated with the hydrates on a microscopic scale
K_RD: K_RD
D
R
K
rigidity associated with the capacity with water adsorbed to transmit loads (load bearing
toilets)
ETA_RS
:
ETA_RS
S
R
viscosity connects associated with the mechanism with dissemination within capillary porosity
ETA_IS
:
ETA_IS
S
I
viscosity connects associated with the mechanism with dissemination interlamellaire
ETA_RD
:
ETA_RD
D
R
viscosity associated with the water adsorbed by the layers with hydrates

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
80/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
ETA_ID
:
ETA_ID
D
I
viscosity of interstitial water.
Note:
The curve of desorption giving the hygroscopy H according to the water C concentration
must be well informed under key word ELAS_FO.
7.15 Key words factor
BETON_ECRO_LINE
Definition of a linear curve of work hardening with taking into account of containment in the case
specific to the concrete. In order to improve behavior in compression one defines a threshold of
reversibility
7.15.1 Syntax
|
BETON_ECRO_LINE = _F
(
D_SIGM_EPSI
=
dsde, [R]
SYT
=
sigt,
[R]
SYC
=
sigc,
[R]
)
7.15.2 Operands
D
_
SIGM_EPSI = dsde (AND)
Slope of the traction diagram.
SYT = sigt
Maximum stress in simple traction.
SYC = sigm
Maximum stress in simple compression (it does not exist for a Poisson's ratio
=0,
in this case one does not specify SYC)
The Young modulus E is to be specified by the key words
ELAS
or
ELAS_FO
.
7.16 Key words factor
GLRC
Definition of the behavior of the concrete plates written in generalized efforts. GLRC is a model
elastoplastic in aggregate variables for orthotropic hulls with possible taking into account of
the influence of the membrane effort on the yield stresses in bending.
7.16.1 Syntax
/
GLRC = _F (
MEX1
=
mex1, [R]
MEY1
=
mey1, [R]
MEX2
=
mex2, [R]
MEY2
=
mey2, [R]
CX1 = cx1, [R]
CY1 = cy1, [R]
CXY1 = cxy1, [R]
CX2 = cx2, [R]
CY2 = cy2, [R]
CXY2 = cxy2, [R]
)

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
81/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
/
GLRC_FO = _F (
MEX1 = mex1
, [function ++]
MEY1 = mey1
, [function ++]
MEX2 = mex2
, [function ++]
MEY2 = mey2
, [function ++]
CX1 = cx1, [function ++]
CY1 = cy1, [function ++]
CXY1 = cxy1, [function ++]
CX2 = cx2, [function ++]
CY2 = cy2, [function ++]
CXY2 = cxy2, [function ++]
)
7.16.2 Operands
MEX1 = mex1
moment limits elastic in positive bending in X.
MEY1 = mey1
moment limits elastic in positive bending in Y.
MEX2 = mex2
moment limits elastic in negative bending in X.
MEY2 = mey2
moment limits elastic in negative bending in Y.
CX1 = cx1
kinematic coefficient of recall in positive bending.
CY1 = cy1
kinematic coefficient of recall in positive bending.
CXY1 = cxy1
kinematic coefficient of recall in positive bending.
CX2 = cx2
kinematic coefficient of recall in negative bending.
CY2 = cy2
kinematic coefficient of recall in negative bending.
CXY2 = cxy2
kinematic coefficient of recall in negative bending.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
82/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
7.17 Word
key
JOINT_BA
This model of nonlinear behavior of the steel-concrete connection is employed for the fine calculation of
concrete structures reinforced where the prediction with the fissures and redistribution with the stresses in the concrete
are very important. Available for analyzes under the effect of monotonous loadings and
cyclic, the model is written within the thermodynamic framework of formulation of the processes
irreversible. It makes it possible to take account of the damage of the interface in shearing, in
combination with the effects of the friction of the fissures, as well as unrecoverable deformations.
document [R7.01.21] described the corresponding details.
This model must be employed with the elements “gasket” in 2D [R3.06.09]. Steel reinforcements
could be modelized with plane elements (QUAD4) or unidimensional (BAR).
Note:
The taking into account of the effect of a thermal loading is not possible for the moment.
7.17.1 Syntax
/
JOINT_BA =
_F (
HPEN =
HPEN,
[R]
GTT
=
GTT
,
[R]
GAMD0
=
0
,
[R]
AD1
=
ad1
,
[R]
BD1
=
bd1
,
[R]
GAMD2
=
2
,
[R]
AD2
=
ad2
,
[R]
BD2
=
bd2
,
[R]
VIFROT
=
vifrot
,
[R]
F
=
alpha
,
[R]
FC
=
C
,
[R]
EPSTR0
=
NR
,
[R]
ADN
=
ADN
,
[R]
BDN
=
bdn
,
[R]
);
7.17.2 Operands
HPEN = HPEN
Parameter of penetration between surfaces by crushing of the concrete.
It is checked that
HPEN > 0.0
E+0.
GTT = GTT
Modulate rigidity of the connection.
It is checked that
G
concrete
GTT
G
steel
.
GAMD0 = 0
Threshold of perfect adherence or limit of elastic strain.
It is checked that
1.E-4
GAMD0
1.E-2.
AD1
=
ad1
Parameter of evolution of the damage in area 1 (passage of small
deformations with the great slips).
It is checked that
1.E-1
AD1
1.E+1.
BD1
=
bd1
Parameter of power describing the evolution of the variable of damage in area
1 (passage of the small deformations to the great slips).
It is checked that
BD1
1.E-1.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
83/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
GAMD2 = 2
Threshold of the great slips.
It is checked that
1.E-4
GAMD2
1.E+0.
AD2
=
ad2
Parameter of evolution of the damage in area 2 (maximum resistance of
connection and degradation in friction).
It is checked that
AD2
1.E-6.
BD2
=
bd2
Parameter of power describing the evolution of the variable of damage in area
2 (maximum resistance of the connection and degradation in friction).
It is checked that
BD2
1.E-1.
VIFROT
= vifrot
Parameter material describing the influence of the friction of the fissures.
It is checked that
VIFROT
0.0
E+0.
F = alpha
Parameter material related to kinematic work hardening by friction of the fissures.
It is checked that
F
0.0
E+0.
FC = C
Parameter describing the influence of containment on the resistance of the connection.
It is checked that
FC
0.0
E+0.
EPSTR0
=
NR
Threshold of elastic strain on the normal direction before the rupture.
It is checked that
1.E-4
EPSTR0
1.E+0.
ADN
=
ADN
Parameter of the damage in the normal direction by opening of the fissure.
It is checked that
ADN
1.E-10.
BDN
=
bdn
Parameter of power describing the evolution of the variable of damage in
normal direction.
It is checked that
BDN
1.E-1.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
84/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
8 Behaviors
Metal-worker-mechanics
For the metallurgical behavior (cf [R4.04.01]), two laws of behavior are available: one
law characteristic of the metallurgical transformations of steel and a law characteristic of alloys
of zirconium.
For the mechanical effects and the associated behaviors, the models are common for steel and
zirconium (cf [R4.04.02]).
8.1
Key word factor
META_ACIER
Parameters to be informed for the metallurgy of steel.
8.1.1 Syntax
|
META_ACIER
=
_F
(
TRC = nomtrc,
[trc]
AR3 = ar3,
[R]
ALPHA =
alpha
,
[R]
MS0 = mso,
[R]
AC1 = ac1,
[R]
AC3 = ac3,
[R]
TAUX_1
=
T1
,
[R]
TAUX_3
=
T3
,
[R]
LAMBDA0= l0,
[R]
QSR_K = Qapp,
[R]
D10 = d10,
[R]
WSR_K = Wapp,
[R]
)
8.1.2 Operands for the phase shifts
TRC = nomtrc
Concept of the type
trc
product by the operator
DEFI_TRC
[U4.43.04] and containing the whole of
information provided by the diagrams
TRC
(Transformation into Continuous Cooling) of
steel considered.
AR3 = ar3
Quasi-static temperature of beginning of decomposition of austenite to cooling.
ALPHA
=
alpha
Coefficient
law of Koïstinen-Marbürger expressing the quantity of martensite formed in
function of the temperature:
(
)
(
)
Z
M
T
M
S
exp
=
-
-
1
.
MSO = mso
Martensitic initial temperature of transformation when the aforementioned is total. In this case
0
S
S
M
M
=
.
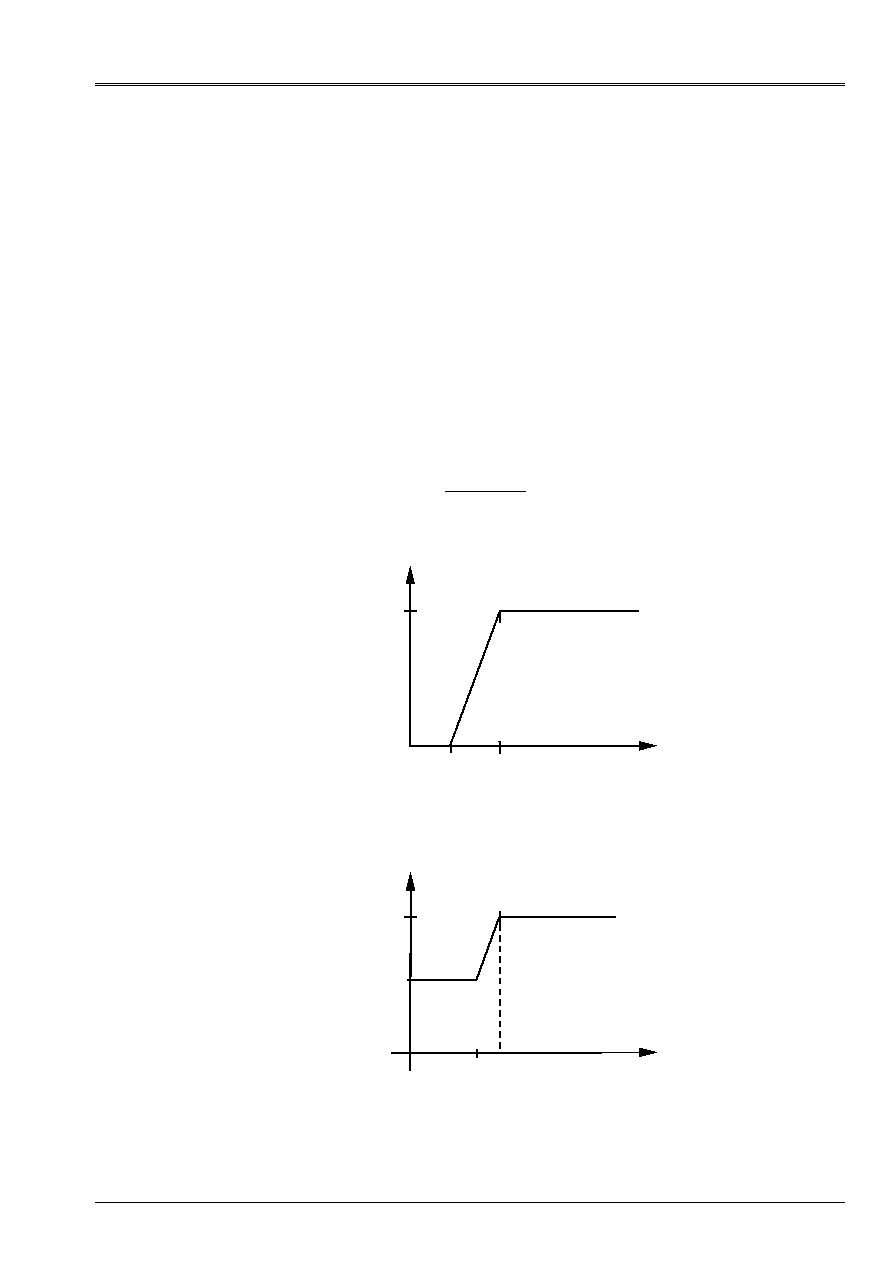
Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
85/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
AC1 = ac1
Quasi-static temperature of beginning of transformation into austenite with the heating.
AC3 = ac3
Quasi-static temperature of end of transformation into austenite.
TAUX_1 = T1
Value of the function “delay” (cf [R4.04.01])
()
(
)
T
intervening in the model of transformation
austenitic at the temperature
AC1
.
TAUX_3 = T3
Value of the function “delay” (cf [R4.04.01])
()
(
)
T
intervening in the model of transformation
austenitic at the temperature
AC3
.
The evolution of the proportion of austenite is then defined by:
()
()
T
T
Z
Z
Z
eq
-
=
&
with:
()
T
Z
eq
and
()
T
Ac1
T3
Ac3
T1
Ac1
T
1
Ac3

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
86/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
8.1.3 Operands for the size of grains
The four operands following involve the calculation of size of grains if they are indicated.
LAMBDA0
=
0
Parameter material intervening in the model of evolution of size of grain below.
dD
dt
D
D
Q
RT
D
D
W
RT
app
app
=
-
=
=
-
1 1
1
0
10
lim
exp
exp
lim
with
QSR_K = Qapp
Parameter energy of activation intervening in the model of evolution of size of grain.
D10 = D10
Parameter material intervening in the model of evolution of size of grain.
WSR_K = Wapp
Parameter energy of activation intervening in the model of evolution of size of grain.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
87/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
8.2
Key word factor META_ZIRC
Parameters to be informed for the metallurgy of the zircaloy (cf [R4.04.01]).
8.2.1 Syntax
| META_ZIRC = _F
(
TDEQ = teqd, [R]
NR = N, [R]
K = K, [R]
QSR_K = qsr
, [R]
CCT
=
CCT
, [R]
AC
= ac,
[R]
M = m, [R]
TDR
=
tdr
, [R]
AR
= Ar,
[R]
Br
= Br,
[R]
8.2.2 Operands
TDEQ = teqd
Initial temperature of transformation
with balance
: compact phase cold hexagonal
: phase hot cubic centered
N = N
Parameter material relating to the model giving the proportion of
according to the temperature, with
balance.
K = K
Parameter material relating to the model giving the proportion of
according to the temperature, with
balance.
CCT = CCT
Initial temperature of transformation
in
with the heating.
AC = ac
Parameter material intervening in the model of evolution of
with the heating.
M = m
Parameter material intervening in the model of evolution of
with the heating.
TDR = tdr
Initial temperature of transformation
in
with cooling.
AR = Ar
Parameter material intervening in the model of evolution of
with cooling.
Br = Br
Parameter material intervening in the model of evolution of
with cooling.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
88/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
8.3
Key word factor
DURT_META
Definition of the characteristics relating to the calculation of hardness associated with the metallurgy with steels.
8.3.1 Syntax
|
DURT_META
=
_F
(
F1_DURT = HVf1, [R]
F2_DURT = HVf2, [R]
F3_DURT = HVf3, [R]
F4_DURT = HVf4, [R]
C_DURT
= HVa
,
[R]
)
8.3.2 Operands
Hardness is calculated by using a linear law of mixture on the microhardness of the components:
HV
Z
HV
I
I
I
=
×
HV
I
: microhardness of component I
Z
I
: proportion of component I
F1_DURT =
HVf1
microhardness of the cold phase F1 (ferrite for steel)
F2_DURT =
HVf2
microhardness of the cold phase F2 (pearlite for steel)
F3_DURT =
HVf3
microhardness of the cold phase F3 (bainite for steel)
F4_DURT =
HVf4
microhardness of the cold phase F4 (martensite for steel)
C_DURT
=
HVf1
microhardness for the hot phase (austenite for steel)

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
89/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
8.4
Key words factor ELAS_META/ELAS_META_FO
Definition of the elastic characteristics, dilation and elastic limits for modeling
of an undergoing material of the metallurgical transformations (see [R4.04.02]). These coefficients can
to be are constant compared to temperature ELAS_META, are to depend on the temperature
ELAS_META_FO (parameter “TEMP”).
Certain coefficients depend on the metallurgical structure (parameter “META”).
For all the relations of behavior relating to materials undergoing of the transformations
metallurgical (ELAS_META, META_ *** _ ***), one can treat two types of materials; the first
corresponds to steels and second is specific to Zircaloy. Various relations (ELAS_META,
META_ *** _ ***) are identical for these two materials (the same phenomena are treated) but it
a many involved phases are different. One chooses material desired while activating, in
the operator STAT_NON_LINE, the key word RELATION_KIT which is worth “STEEL” or “ZIRC”.
·
steel can comprise (with more) five different metallurgical phases (cold phase 1 =
ferrite, cold phase 2 = pearlite, cold phase 3 = bainite, cold phase 4 = martensite and one
hot phase = austenite),
·
the zircaloy can comprise (with more) three different metallurgical phases (cold phase 1 =
phase
pure, cold phase 2 = phase
mix and a hot phase = phase
.
Consequently, for a steel one informs to the maximum 5 elastic limits whereas with Zircaloy
one does not inform any to the maximum three.
8.4.1 Syntax
|
ELAS_META = _F
(
E
=
Young
,
[R]
NAKED
=
naked
,
[R]
F_ALPHA =
F
,
[R]
C_ALPHA =
,
[R]
PHASE_REFE =
/“HOT”,
[TXM]
/“COLD”,
EPSF_EPSC_TREF =
,
[R]
TEMP_DEF_ALPHA = T
,
[R]
PRECISION
=
/
,
[R]
/1.
, [DEFECT]
F1_SY
=
F_
y1
,
[R]
F2_SY
=
F_
y2
,
[R]
F3_SY
=
F_
y3
,
[R]
F4_SY
=
F_
y4
,
[R]
C_SY =
F_
y
,
[R]
SY_MELANGE =
F,
[function]
F1_S_VP =
F_
c1
,
[R]
F2_S_VP =
F_
c2
,
[R]
F3_S_VP =
F_
c3
,
[R]
F4_S_VP =
F_
c4
,
[R]
C_S_VP
=
F_
C
,
[R]
S_VP_MELANGE
=
F,
[function]
)

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
90/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
|
ELAS_META_FO
=_F
(
E
=
Young
,
[function **]
NAKED
=
naked
,
[function **]
F_ALPHA =
F
,
[function **]
C_ALPHA =
,
[function **]
PHASE_REFE =
/“HOT”,
[TXM]
/“COLD”,
EPSF_EPSC_TREF =
,
[R]
TEMP_DEF_ALPHA = T
,
[R]
PRECISION
=
/
,
[R]
/1.
, [DEFECT]
F1_SY
=
F_
y1
,
[function **]
F2_SY
=
F_
y2
,
[function **]
F3_SY
=
F_
y3
,
[function **]
F4_SY
=
F_
y4
,
[function **]
C_SY =
F_
y
,
[function **]
SY_MELANGE =
F,
[function]
F1_S_VP =
F_
c1
,
[function **]
F2_S_VP =
F_
c2
,
[function **]
F3_S_VP =
F_
c3
,
[function **]
F4_S_VP =
F_
c4
,
[function **]
C_S_VP
=
F_
C
,
[function **]
S_VP_MELANGE
=
F,
[function]
)
8.4.2 Operands
E = Young
Young modulus, identical for all the metallurgical phases.
NAKED = naked
Poisson's ratio, identical for all the metallurgical phases.
F_ALPHA =
F
Thermal expansion factor average of the cold phases.
C_ALPHA
=
Thermal expansion factor average of the hot phase.
PHASE_REFE =
/“HOT”
/“COLD”
Choice of the metallurgical phase of reference (hot phase or cold phase).
Indeed, to define the null thermal deformation, it is necessary to define the temperature of Tref reference
(defined in AFFE_MATERIAU) and the metallurgical phase of reference, so that
thermal deformation is considered null in Tref and in the metallurgical state of reference.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
91/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
EPSF_EPSC_TREF =
Deformation of the phase not of reference compared to the phase of reference to the temperature
ref.
T
: translated the difference in compactness between the cubic crystallographic structures with faces
centered (standard austenitic) and cubic centered (standard ferritic).
TEMP_DEF_ALPHA = T
Temperature compared to which one defines the expansion factor. If C_ALPHA
is a function, this operand is obligatory.
PRECISION
This reality indicates with which precision a temperature
T
is close to the temperature to
reference (cf [§3.1.4]).
F1_SY
=
F_sigm_f
Elastic limit of the cold phase 1 for a plastic behavior.
F2_SY
=
F_sigm_f
Elastic limit of the cold phase 2 for a plastic behavior.
F3_SY
=
F_sigm_f
Elastic limit of the cold phase 3 for a plastic behavior.
F4_SY
=
F_sigm_f
Elastic limit of the cold phase 4 for a plastic behavior.
C_SY =
F_sigm_f
Elastic limit of the hot phase for a plastic behavior.
SY_MELANGE = F
Function used for the law of mixture on the elastic limit of multiphase material for one
plastic behavior.
()
(
)
()
y
y
y
F Z
F Z
= -
+
1
F1_S_VP =
F_sigm_f
Elastic limit of the cold phase 1 for a viscous behavior.
F2_S_VP =
F_sigm_f
Elastic limit of the cold phase 2 for a viscous behavior.
F3_S_VP =
F_sigm_f
Elastic limit of the cold phase 3 for a viscous behavior.
F4_S_VP =
F_sigm_f
Elastic limit of the cold phase 4 for a viscous behavior.
C_S_VP
=
F_sigm_f
Elastic limit of the hot phase for a viscous behavior.
S_VP_MELANGE
= F
Function used for the law of mixture on the elastic limit of multiphase material for one
viscous behavior.
()
(
)
()
y
y
y
F Z
F Z
= -
+
1
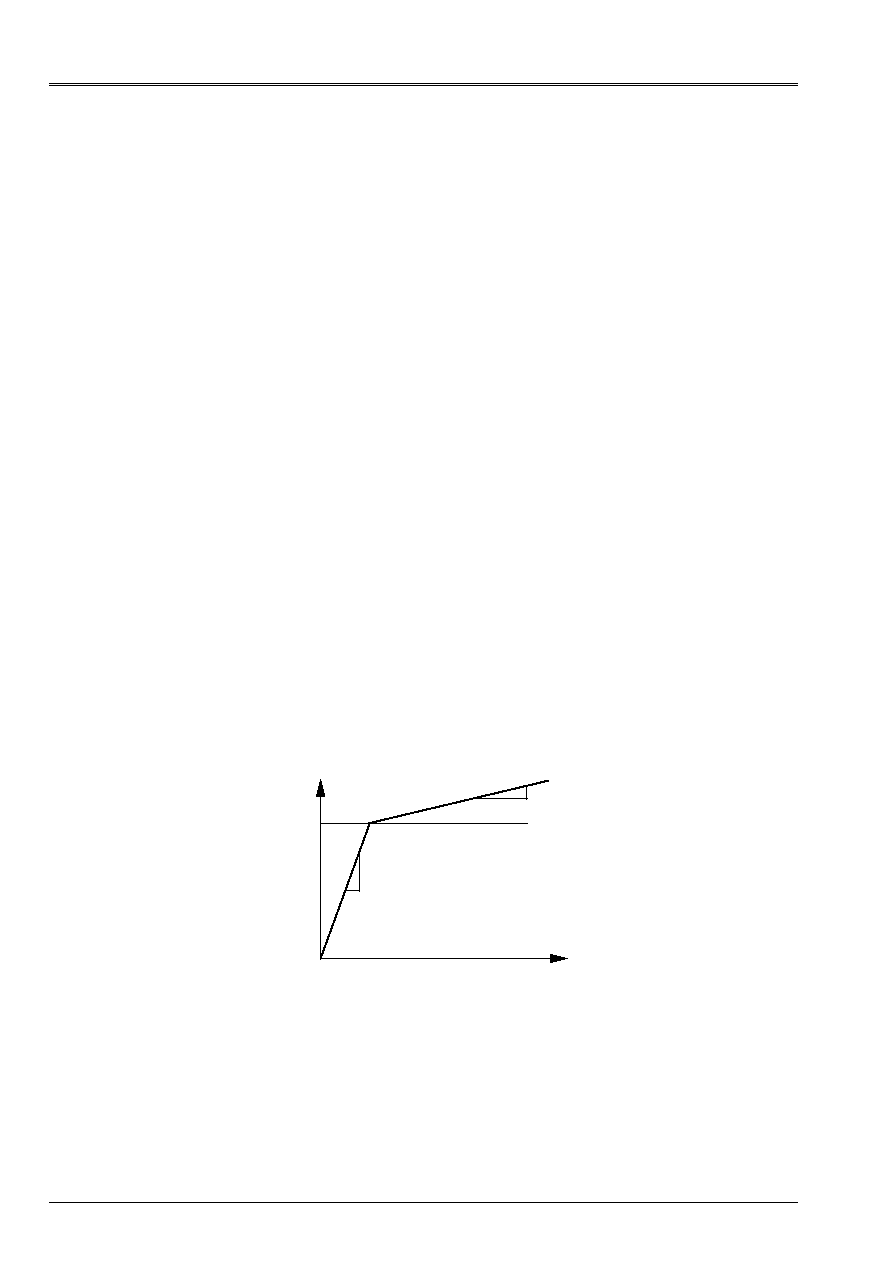
Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
92/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
8.5
Key word factor META_ECRO_LINE
Definition of five modules of work hardening used in the modeling of the phenomenon of work hardening
isotropic linear of an undergoing material of the metallurgical phase shifts (see [R4.04.02]).
These modules depend on the temperature.
8.5.1 Syntax
|
META_ECRO_LINE = _F (
F1_D_SIGM_EPSI = dsde, [function **]
F2_D_SIGM_EPSI = dsde, [function **]
F3_D_SIGM_EPSI = dsde, [function **]
F4_D_SIGM_EPSI = dsde, [function **]
C_D_SIGM_EPSI
=
dsde,
[function **]
)
8.5.2 Operands
F1_D_SIGM_EPSI = dsde
Slope of the traction diagram for the cold phase 1.
F2_D_SIGM_EPSI = dsde
Slope of the traction diagram for the cold phase 2.
F3_D_SIGM_EPSI = dsde
Slope of the traction diagram for the cold phase 3.
F4_D_SIGM_EPSI = dsde
Slope of the traction diagram for the cold phase 4.
C_D_SIGM_EPSI
=
dsde
Slope of the traction diagram for the hot phase.
sigm
E
1
dsde
The Young modulus E is to be specified by key words META_
ELAS
or META_ELAS
_FO
.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
93/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
8.6
Key word factor META_TRACTION
Definition of five traction diagrams used in the modeling of the phenomenon of work hardening
isotropic nonlinear of an undergoing material of the metallurgical phase shifts
(see [R4.04.02]). The traction diagrams can possibly depend on the temperature.
8.6.1 Syntax
|
META_TRACTION = _F (
SIGM_F1 = r_p, [function **]
SIGM_F2 = r_p, [function **]
SIGM_F3 = r_p, [function **]
SIGM_F4 = r_p, [function **]
SIGM_C = r_p, [function **]
)
8.6.1.1 Operands
SIGM_F1 =
r_p
Isotropic curve work hardening R according to the cumulated plastic deformation p for
cold phase 1.
SIGM_F2 =
r_p
Isotropic curve work hardening R according to the cumulated plastic deformation p for
cold phase 2.
SIGM_F3 =
r_p
Isotropic curve work hardening R according to the cumulated plastic deformation p for
cold phase 3.
SIGM_F4 =
r_p
Isotropic curve work hardening R according to the cumulated plastic deformation p for
cold phase 4.
SIGM_C
=
r_p
Isotropic curve work hardening R according to the cumulated plastic deformation p for
hot phase.
Note:
Attention it is not a question of the curve
function of
but of the curve R function of p.
One passes from the one to the other by carrying out following calculations: R =
- elastic limit,
p =
(/E).

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
94/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
8.7
Key word factor META_VISC
Definition of the viscous parameters of the viscoplastic law of behavior with taking into account of
metallurgy (see [R4.04.02]). The viscoplastic model of Norton-Hoff type comprises 5 parameters;
parameters conventional
, N of the law of flow in power, yield stress of flow
viscous, the parameters C and m relating to the restoration of work hardening of viscous origin. These
parameters depend on the temperature and the metallurgical structure.
The limit elastic parameters are defined in ELAS_META.
8.7.1 Syntax
|
META_VISC
= _F
(
F1_ETA
=
1,
[function **]
F2_ETA
=
2,
[function **]
F3_ETA
=
3,
[function **]
F4_ETA
=
4,
[function **]
C_ETA
=
5,
[function **]
F1_N = n1
, [function **]
F2_N = N2
, [function **]
F3_N = n3
, [function **]
F4_N = n4
, [function **]
C_N
=
n5
,
[function **]
F1_C = C1
, [function **]
F2_C = C2
, [function **]
F3_C = C3
, [function **]
F4_C = C4
, [function **]
C_C
=
C5
,
[function **]
F1_M = m1
, [function **]
F2_M = m2
, [function **]
F3_M = m3
, [function **]
F4_M = m4
, [function **]
C_M
=
m5
,
[function **]
)
8.7.2 Operands
F1_ETA
=
1
Parameter
viscoplastic law of flow, for the cold phase 1.
F2_ETA
=
2
Parameter
viscoplastic law of flow, for the cold phase 2.
F3_ETA
=
3
Parameter
viscoplastic law of flow, for the cold phase 3.
F4_ETA
=
4
Parameter
viscoplastic law of flow, for the cold phase 4
C_ETA
=
5
Parameter
viscoplastic law of flow, for the hot phase

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
95/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
F1_N = n1
Parameter N of the viscoplastic law of flow, for the cold phase 1.
F2_N = N2
Parameter N of the viscoplastic law of flow, for the cold phase 2.
F3_N = n3
Parameter N of the viscoplastic law of flow, for the cold phase 3.
F4_N = n4
Parameter N of the viscoplastic law of flow, for the cold phase 4
C_N
=
n5
Parameter N of the viscoplastic law of flow, for the hot phase
F1_C = C1
Parameter C relating to the restoration of work hardening of viscous origin, for the cold phase 1.
F2_C = C2
Parameter C relating to the restoration of work hardening of viscous origin, for the cold phase 2.
F3_C = C3
Parameter C relating to the restoration of work hardening of viscous origin, for the cold phase 3.
F4_C = C4
Parameter C relating to the restoration of work hardening of viscous origin, for the cold phase 4
C_C
=
C5
Parameter C relating to the restoration of work hardening of viscous origin, for the hot phase
F1_M = m1
Parameter m relating to the restoration of work hardening of viscous origin, for the cold phase 1.
F2_M = m2
Parameter m relating to the restoration of work hardening of viscous origin, for the cold phase 2.
F3_M = m3
Parameter m relating to the restoration of work hardening of viscous origin, for the cold phase 3.
F4_M = m4
Parameter m relating to the restoration of work hardening of viscous origin, for the cold phase 4
C_M
=
m5
Parameter m relating to the restoration of work hardening of viscous origin, for the hot phase

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
96/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
8.8
Key word factor
META_PT
Definition of the characteristics used in the modeling of the plasticity of transformation of one
material which undergoes metallurgical phase shifts (see [R4.04.02]).
The model is as follows:
()
Pt
I I
I
I
I
I
K F Z
Z
=
<
>
=
=
3
2
1
4
'
8.8.1 Syntax
/
META_PT
=
_F
(
F1_K
=
KF
,
[R]
F2_K
=
Kp
,
[R]
F3_K
=
KB
,
[R]
F4_K
=
Km
,
[R]
F1_D_F_META = F' F,
[function **]
F2_D_F_META = F' p,
[function **]
F3_D_F_META = F' B,
[function **]
F4_D_F_META = F' m,
[function **]
)
8.8.2 Operands
F1_K = KF
F2_K = Kp
F3_K = KB
F4_K = km
Ki constants used in the model of plasticity of transformation, for the different ones
cold phases. For steel; phase ferritic, perlitic, bainitic and martensitic.
F1_D_F_META=F' F F2_D_F_META=F' p F3_D_F_META=F' B
F4_D_F_META=F' m
Functions
'
I
F
used in the model of plasticity of transformation, for the different ones
cold phases. For steel; phase ferritic, perlitic, bainitic and martensitic.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
97/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
8.9
Key word factor
META_RE
Definition of the characteristics used in the modeling of the phenomenon of restoration
of work hardening of a material which undergoes metallurgical phase shifts (see [R4.04.02]).
8.9.1 Syntax
/
META_RE
=
_F
(
C_F1_THETA =
F
[R]
C_F2_THETA =
p
[R]
C_F3_THETA =
B
[R]
C_F4_THETA =
m
[R]
F1_C_THETA =
F
[R]
F2_C_THETA =
p
[R]
F3_C_THETA =
B
[R]
F4_C_THETA =
m
[R]
)
8.9.2 Operands
C_F1_THETA=
F C_F2_THETA=
PC _F3_THETA=
B C_F4_THETA=
m
Constants characterizing the rate of work hardening transmitted at the time of the transformation of the phase
hot C in cold phase. For steel; transformation of austenite into ferrite, pearlite,
bainite and martensite. Thus,
= 0 correspond to a total restoration and = 1 with one
total transmission of work hardening.
F1_C_THETA=
F
F2_C_THETA=
p
F3_C_THETA=
B
F4_C_THETA=
m
Constants characterizing the rate of work hardening transmitted at the time of the transformation of the phases
cold in hot phase. For steel; transformation of ferrite, the pearlite, bainite
and of austenite martensite. Thus,
= 0 correspond to a total restoration and = 1 with
a total transmission of work hardening.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
98/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
9 HYDRO-MECHANICAL THERMO Behaviors and of
grounds
9.1
Single-ended spanner word COMP_THM
Allows to select as of the definition of material the mixing rate THM.
The table below specifies the obligatory key words according to the selected mixing rate.
LIQU_SATU
LIQU_GAZ
GAS
LIQU_GAZ_AT
M
LIQU_VAPE_GAZ
LIQU_AD_GAZ_VAPE LIQU_VAPE
THM_INIT
O
O
O
O
O
O
O
PRE1 O
O
O
O
O
O
O
PRE2
O
O
O
PORO O
O
O
O
O
O
O
TEMP T
O
O
T
O
O
O
PRES_VAPE
O
O
O
THM_DIFFU
O
O
O
O
O
O
O
R_GAZ
O
O
O
O
O
RHO O
O
O
O
O
O
O
BIOT_COEF O
O
O
O O
O O
PESA_X O
O
O
O
O O
O
PESA_Y O
O
O
O
O O
O
PESA_Z O
O
O
O
O O
O
SATU_PRES
O
I
O
O
O
O
D_SATU_PRES
O
I
O
O
O
O
PERM_LIQU
I
O
I
O
O
O
O
D_PERM_LIQU_SATU
O
O
O
O
O
PERM_GAZ
O
O
O
O
D_PERM_SATU_GAZ
O
O
O
O
D_PERM_PRES_GAZ
O
O
O
O
FICKV_T
O
O
FICKV_PV
FICKV_PG
FICKV_S
D_FV_T
D_FV_PG
FICKA_T
O
FICKA_PA
FICKA_PL
FICKA_S
D_FA_T
CP T
T
T
T
T
T
T
PERM_IN/PERM_END
/PERM_X
O O
O O
O
O
O
PERM_Y
PERM_Z
LAMB_T T
T
T
T
T T
T
LAMB_S
LAMB_PHI
LAMB_CT
D_LB_T
D_LB_S
D_LB_PHI
THM_LIQU
O
O
O
O
O
O
RHO O
O
O
O
O
O
UN_SUR_K O
O
O O
O O
VISC O
O
O
O
O
O
D_VISC_TEMP O
O
O
O
O
O
ALPHA T
T
T
T
T
T
CP T
T
T
T
T
T
THM_GAZ
O
O
O
O
O
MASS_MOL
O
O
O O O
VISC
O
O
O
O
O
D_VISC_TEMP
O
O
O O
O
CP
T
T
T
T
T
THM_VAPE_GAZ
O
O
O
MASS_MOL
O O O
CP
O
O
O
VISC
O
O
O
D_VISC_TEMP
O
O
O
THM_AIR_DISS
O
CP
O
COEF_HENRY
O
Legends:
O
: Obligatory key word
T
: Obligatory key word in Thermics
: Useless key word for this type of mixing rate
Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
99/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
Syntax is as follows:
COMP_THM =
/`LIQU_SATU `,
/`LIQU_GAZ `,
/`GAS `,
/`LIQU_GAZ_ATM `,
/`LIQU_VAPE_GAZ `,
/`LIQU_AD_GAZ_VAPE `,
/`LIQU_VAPE `,
/`LIQU_SATU_GAT `,
/`LIQU_NSAT_GAT `,
/
`LIQU_AD_GAZ_VAPE `
,
9.2
Key word factor THM_INIT
For all the ThermoHydroMécaniques behaviors, it makes it possible to describe the initial state of the structure
(cf [R7.01.11] and [R7.01.14]).
9.2.1 Syntax
THM_INIT = _F
(
TEMP =
temp
,
[R]
PRE1
= pre1,
[R]
PRE2 =
pre2
,
[R]
PORO =
poro
,
[R]
PRES_VAPE
=
pvap
, [R]
DEGR_SATU
=
ds, [R]
PRES_ATMO
=
patm
, [R]
)
For including/understanding these data well, it is necessary to distinguish the unknown factors with the nodes, which we call
{}
U
ddl
and values defined under the key word THM_INIT which we call
p
ref.
and
T
ref.
.
{}
U
U
U
U
ddl
X
y
Z
ddl
ddl
=
PRE1
PRE 2
The significance of unknown factors PRE1 and PRE2 varies according to the models. While noting
W
p
pressure
of water,
AD
p
pressure of dissolved air,
p
L
pressure of fluid
AD
W
L
p
p
p
+
=
,
have
p
pressure of air
dryness
p
vp
the steam pressure,
vp
have
G
p
p
p
+
=
total gas pressure and
p
p
p
C
G
L
=
-
capillary pressure (also called suction), one has the following significances of unknown factors PRE1 and
PRE2:
Behavior
KIT
LIQU_SATU
LIQU_GAZ_ATM GAS LIQU_VAPE_GAZ LIQU_GAZ LIQU_AD_GA
Z_VAPE
PRE1
p
L
- p
L
p
G
p
p
p
C
G
L
=
-
p
p
p
C
G
L
=
-
p
p
p
C
G
L
=
-
PRE2
p
G
p
G
p
G

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
100/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
One will be able to refer to [§3.3.2.3] documentation of control STAT_NON_LINE
[U4.51.03].
One then defines the “total” pressures and the temperature by:
p
p
p
T
T
T
ddl
ref.
ddl
ref.
=
+
=
+
;
The values written by IMPR_RESU are the nodal unknown factors
p
T
ddl
ddl
and
. In the same way them
boundary conditions must be expressed compared to the nodal unknown factors.
On the other hand, in fact the pressures and the total air temperature are used in the laws of
behavior
p
R
MR. T
=
for perfect gases,
D
dp
K
dT
L
L
L
L
L
=
- 3
for the fluid and in
relation capillary saturation/pressure.
Let us note that the nodal values can be initialized by key word ETAT_INIT of the control
STAT_NON_LINE.
The user must be very careful in the definition of the values of THM_INIT: indeed, the definition of
several materials with values different from the quantities defined under THM_INIT leads to
discontinuous values initial of the pressure and the temperature, which is not in fact not compatible
with the general processing which is made of these quantities. We thus advise with the user
following step:
·
if at the beginning, there is a uniform field of pressure or of temperature, one re-enters it directly
by key word THM_INIT,
·
if there is a nonuniform field, one enters for example a reference by key word THM_INIT
control initial DEFI_MATERIAU, and values compared to this reference by
key word ETAT_INIT of control STAT_NON_LINE.
9.2.2 Operand
TEMP
Temperature of reference
ref.
T
.
The value of the temperature of reference entered behind key word TEMP_REF of the control
AFFE_MATERIAU is ignored.
9.2.3 Operand
PRE1
For the behaviors: LIQU_SATU, ELAS_THM and pressure of fluid of reference.
For the behavior: GAS pressure of standard gas.
For the behavior: LIQU_GAZ_ATM pressure of fluid of changed reference of sign.
For the behaviors: LIQU_VAPE_GAZ, LIQU_AD_GAZ_VAPE and capillary LIQU_GAZ pressure
of reference.
9.2.4 Operand
PRE2
For the behaviors: LIQU_VAPE_GAZ, LIQU_AD_GAZ_VAPE and LIQU_GAZ and pressure of gas
of reference.
9.2.5 Operand
PORO
Initial porosity.
9.2.6 Operand
PRES_VAPE
For the behaviors: LIQU_VAPE_GAZ, LIQU_AD_GAZ_VAPE and LIQU_GAZ and pressure of
initial vapor.
9.2.7 Operand
DEGR_SATU
For all the unsaturated behaviors: initial degree of saturation.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
101/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
9.3
Key word factor THM_LIQU
This key word relates to all behaviors THM utilizing a fluid (cf [R7.01.11]).
9.3.1 Syntax
THM_LIQU = _F
(
RHO
=
rho
,
[R]
UN_SUR_K
=
usk
,
[R]
ALPHA
=
alp
,
[R]
CP
=
CP,
[R]
VISC =
VI,
[function
**]
D_VISC_TEMP = dvi,
[function **]
)
9.3.2 Operand
RHO
Density of the fluid for the pressure defined under key word PRE1 of the key word factor
THM_INIT.
9.3.3 Operand
UN_SUR_K
Opposite of the compressibility of the fluid:
K
L
.
9.3.4 Operand ALPHA
Expansion factor of the fluid
L
If
p
L
indicate the pressure of the fluid,
L
its density and
T
the temperature, the behavior
fluid is:
D
dp
K
dT
L
L
L
L
L
=
- 3
9.3.5 Operand CP
Specific heat with constant pressure of the fluid.
9.3.6 Operand VISC
Viscosity of the fluid. Function of the temperature.
9.3.7 Operand
D_VISC_TEMP
Derived from the viscosity of the fluid compared to the temperature. Function of the temperature. The user
must ensure coherence with the function associated with VISC.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
102/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
9.4
Key word factor THM_GAZ
This key word factor relates to all behaviors THM utilizing a gas (cf [R7.01.11]).
For the behaviors utilizing at the same time a fluid and a gas, and when one takes into account
the evaporation of the fluid, the coefficients indicated here relate to dry gas. Properties of
vapor are indicated under key word THM_VAPE_GAZ.
9.4.1 Syntax
THM_GAZ = _F (
MASS_MOL
=
Mgs
,
[R]
CP
=
CP,
[R]
VISC =
VI,
[function
**]
D_VISC_TEMP
=
dvi
,
[function
**]
)
9.4.2 Operand
MASS_MOL
Mass molar dry gas.
M
gs
If
p
gs
indicate the pressure of dry gas,
gs
its density,
R
the constant of perfect gases and
T
the temperature, the reaction of dry gas is:
p
RT
M
gs
gs
gs
=
.
9.4.3 Operand CP
Specific heat with constant pressure of dry gas.
9.4.4 Operand
VISC
Viscosity of dry gas. Function of the temperature.
9.4.5 Operand
D_VISC_TEMP
Derived compared to the temperature from viscosity from dry gas. Function of the temperature.
The user must ensure coherence with the function associated with VISC.
9.5
Key word factor THM_VAPE_GAZ
This key word factor relates to all behaviors THM utilizing at the same time a fluid and one
gas, and fascinating of account the evaporation of the fluid (cf [R7.01.11]). Coefficients indicated here
relate to the vapor.
9.5.1 Syntax
THM_VAPE_GAZ = _F
(
MASS_MOL =
m
,
[R]
CP
=
CP,
[R]
VISC =
VI,
[function
**]
D_VISC_TEMP = dvi,
[function **]
)

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
103/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
9.5.2 Operand
MASS_MOL
Mass molar vapor.
M
vp
If is
M
vp
indicate the pressure of the vapor,
vp
its density,
R
the constant of perfect gases
and
T
the temperature, the behavior of the vapor is:
p
RT
M
vp
vp
vp
=
9.5.3 Operand
CP
Specific heat with constant pressure of the vapor.
9.5.4 Operand
VISC
Viscosity of the vapor. Function of the temperature.
9.5.5 Operand
D_VISC_TEMP
Derived compared to the temperature from viscosity from the vapor. Function of the temperature.
The user must ensure coherence with the function associated with VISC.
9.6
Key word factor THM_AIR_DISS
This key word factor relates to fascinating behavior THM THM_AD_GAZ_VAPE of account
dissolution of the air in the fluid (cf [R7.01.11]). The coefficients indicated here relate to the air
dissolved.
9.6.1 Syntax
THM_AD_GAZ_VAPE = _F
(
CP
=
CP,
[R]
COEF_HENRY =
H
,
[function
**]
)
9.6.2 Operand
CP
Specific heat with constant pressure of the dissolved air.
9.6.3 Operand
COEF_HENRY
Constant of Henry
H
K
, allowing to connect the molar concentration of dissolved air
ol
AD
C
(moles/m3) with
pressure of dry air:
H
have
ol
AD
K
p
C
=
9.6.4 Operand
D_VISC_TEMP
Derived compared to the temperature from viscosity from the vapor. Function of the temperature.
The user must ensure coherence with the function associated with VISC.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
104/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
9.7
Key word factor THM_DIFFU
Obligatory for all behaviors THM (cf [R7.01.11]). The user must ensure himself of
coherence of the functions and their derivative.
9.7.1 Syntax
THM_DIFFU = _F
(
R_GAZ
=
rgaz
,
[R]
RHO
=
rho
,
[R]
CP
=
CP,
[R]
BIOT_COEF
=
bio
,
[R]
SATU_PRES
=
sp,
[function]
D_SATU_PRES
=
dsp
,
[function]
PESA_X
=
px,
[R]
PESA_Y
=
py,
[R]
PESA_Z
=
pz,
[R]
PERM_IN =
perm
,
[function]
PERMIN_X
=
OX,
[function]
PERMIN_Y
=
OX,
[function]
PERMIN_Z
=
OX,
[function]
PERM_LIQU
=
perml,
[function]
D_PERM_LIQU_SATU
=
dperm,
[function]
PERM_GAZ
=
permg,
[function]
D_PERM_SATU_GAZ
=
dpsg
,
[function]
D_PERM_PRES_GAZ
=
dppg
,
[function]
FICKV_T =
fvt
,
[function]
FICKV_PV =/
fvpv, [function]
/
1
,
[DEFECT]
FICKV_PG =/fvpg, [function]
/
1
,
[DEFECT]
FICKV_S =
/
fvs
,
[function]
/
1
,
[DEFECT]
D_FV_T
=
/
dfvt,
[function]
/
0
,
[DEFECT]
D_FV_PG =/dfvgp, [function]
/
0
,
[DEFECT]
FICKA_T =
conceited person
,
[function]
FICKA_PA =/fapv, [function]
/
1
,
[DEFECT]
FICKA_PL =/fapg, [function]
/
1
,
[DEFECT]
FICKA_S =
/
fas
, [function]
/
1
,
[DEFECT]
D_FA_T
=
/
dfat,
[function]
/
0
,
[DEFECT]
LAMB_T
=/lambt, [function]
/
0
[DEFECT]
LAMB_S
=/lambs, [function]
/
1
,
[DEFECT]
LAMB_PHI =/lambp, [function]
/
1
,
[DEFECT]
LAMB_CT =/lambct
, [function]
/
0
,
[DEFECT]
D_LB_S
=/dlambs
, [function]
/
0
,
[DEFECT]
D_LB_T
=/dlambt
, [function]
/
0
,
[DEFECT]
D_LB_PHI =/dlambp
, [function]

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
105/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
/
0
,
[DEFECT]
SIGMA_T =
St,
[function]
D_SIGMA_T
=
dst
,
[function]
PERM_G_INTR
=
pgi
,
[function]
CHAL_VAPO
=
cv,
[function
**]
EMMAG
=
EM,
[R]
)
9.7.2 Operand
R_GAZ
Constant of perfect gases.
9.7.3 Operand
RHO
For the hydraulic behaviors homogenized density.
Note:
For modelings utilizing it thermal, one uses also the density of
solid matter constituents, which one reads under key word RHO of the key word factor ELAS.
9.7.4 Operand
CP
For the thermal behaviors specific heat with constant stress of the solid alone.
9.7.5 Operand
BIOT_COEF
Coefficient of Biot.
9.7.6 Operand
SATU_PRES
For the unsaturated material behaviors (LIQU_VAPE_GAZ, LIQU_AD_GAZ_VAPE,
LIQU_GAZ, LIQU_GAZ_ATM), isotherm of saturation function of the capillary pressure.
9.7.7 Operand
D_SATU_PRES
For the unsaturated material behaviors (LIQU_VAPE_GAZ, LIQU_AD_GAZ_VAPE,
LIQU_GAZ, LIQU_GAZ_ATM), derived from saturation compared to the pressure.
9.7.8 Operand
PESA_X
Gravity according to X, used only if the modeling chosen in AFFE_MODELE includes 1 or 2
variable of pressure.
9.7.9 Operand PESA_Y
Gravity according to y, used only if the modeling chosen in AFFE_MODELE includes 1 or 2
variable of pressure.
9.7.10 Operand PESA_Z
Gravity according to Z, used only if the modeling chosen in AFFE_MODELE includes 1 or 2
variable D pressure.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
106/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
9.7.11 Operand PERM_IN
Intrinsic permeability: function of porosity (in the isotropic case).
The permeability to the conventional direction
K
, whose dimension is that a speed is calculated way
following:
G
K
K
K
L
rel
µ
int
=
where
K
int
is the intrinsic permeability,
K
rel
the relative permeability,
µ
viscosity,
L
density of the fluid and
G
the acceleration of gravity.
K
int
in fact one is
diagonal tensor, in the isotropic case its three components are equal to the well informed value.
9.7.12 Operand PERMIN_X
In the orthotropic case, component in X of the intrinsic tensor of permeability. In this case,
PERMIN_Y and PERMIN_Z are obligatory.
9.7.13 Operand PERMIN _Y
In the orthotropic case, component in there of the intrinsic tensor of permeability.
9.7.14 Operand PERMIN _Z
In the orthotropic case, component in Z of the intrinsic tensor of permeability.
9.7.15 Operand PERM_LIQU
Permeability relating to the fluid: function of saturation.
9.7.16 Operand D_PERM_LIQU_SATU
Derived from the Permeability relating to the fluid compared to saturation: function of saturation.
9.7.17 Operand PERM_GAZ
Permeability relating to gas: function of the saturation and the gas pressure.
9.7.18 Operand D_PERM_SATU_GAZ
Derived from the permeability to gas compared to saturation: function of the saturation and of
gas pressure.
9.7.19 Operand D_PERM_PRES_GAZ
Derived from the permeability to gas compared to the gas pressure: function of the saturation and of
gas pressure.
9.7.20 Operand FICKV_T
For behaviors LIQU_VAPE_GAZ and LIQU_AD_GAZ_VAPE, coefficient of Fick function of
temperature for the dissemination of the vapor in the gas mixture. The coefficient of Fick which can be
function of saturation, the temperature, the pressure of gas and the steam pressure, one defines it
like a product of 4 functions: FICKV_T, FICKV_S, FICKV_PG, FICKV_VP. In the case of
LIQU_VAPE_GAZ and LIQU_AD_GAZ_VAPE, only FICKV_T are obligatory.
9.7.21 Operand FICKV_S
For behaviors LIQU_VAPE_GAZ and LIQU_AD_GAZ_VAPE, coefficient of Fick function of
saturation for the dissemination of the vapor in the gas mixture.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
107/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
9.7.22 Operand FICKV_PG
For behaviors LIQU_VAPE_GAZ and LIQU_AD_GAZ_VAPE, coefficient of Fick function of
gas pressure for the dissemination of the vapor in the gas mixture.
9.7.23 Operand FICKV_PV
For behaviors LIQU_VAPE_GAZ and LIQU_AD_GAZ_VAPE, coefficient of Fick function of
steam pressure for the dissemination of the vapor in the gas mixture.
9.7.24 Operand D_FV_T
For behaviors LIQU_VAPE_GAZ and LIQU_AD_GAZ_VAPE, derived from coefficient FICKV_T
compared to the temperature.
9.7.25 Operand D_FV_PG
For behaviors LIQU_VAPE_GAZ and LIQU_AD_GAZ_VAPE, derived from coefficient FICKV_PG
compared to the gas pressure.
9.7.26 Operand FICKA_T
For the behavior LIQU_AD_GAZ_VAPE, coefficient of Fick function of the temperature for
dissemination of the air dissolved in the liquid mixture. The coefficient of Fick which can be a function of
saturation, the temperature, the pressure of dissolved air and the pressure of fluid, one defines it as one
product of 4 functions
: FICKA_T, FICKA_S, FICKV_PA, FICKV_PL. In the case of
LIQU_AD_GAZ_VAPE, only FICKA_T are obligatory.
9.7.27 Operand FICKA_S
For the behavior LIQU_AD_GAZ_VAPE, coefficient of Fick function of saturation for
dissemination of the air dissolved in the liquid mixture.
9.7.28 Operand FICKA_PA
For the behavior LIQU_AD_GAZ_VAPE, coefficient of Fick function of the pressure of dissolved air
for the dissemination of the air dissolved in the liquid mixture.
9.7.29 Operand FICKA_PL
For the behavior LIQU_AD_GAZ_VAPE, coefficient of Fick function of the pressure of fluid
for the dissemination of the air dissolved in the liquid mixture.
9.7.30 Operand D_FA_T
For behavior LIQU_AD_GAZ_VAPE, derived from coefficient FICKA_T compared to
temperature.
9.7.31 Operand LAMB_T
For multiplicative behavior THER_POLY left the thermal conductivity of the mixture
depending on the temperature (cf [R7.01.11]).
For thermal behavior THER_HOMO conductivity of the mixture.
This operand is obligatory in the thermal case.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
108/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
9.7.32 Operand LAMB_S
For multiplicative behavior THER_POLY left (equal to 1 per defect) conductivity
thermics of the mixture depend on saturation (cf [R7.01.11]).
9.7.33 Operand LAMB_PHI
For multiplicative behavior THER_POLY left (equal to 1 per defect) conductivity
thermics of the mixture depend on porosity (cf [R7.01.11]).
9.7.34 Operand LAMB_CT
For behavior THER_POLY left the thermal conductivity of the constant mixture and
additive (cf [R7.01.11]). This constant is equal to zero per defect.
9.7.35 Operand D_LB_T
For behavior THER_POLY derived from the part of thermal conductivity of the mixture
depending on the temperature compared to the temperature.
For behavior THER_HOMO derived from the thermal conductivity of the mixture compared to
temperature.
9.7.36 Operand D_LB_S
For behavior THER_POLY derived from the part of thermal conductivity of the mixture
depending on saturation.
9.7.37 Operand D_LB_PHI
For behavior THER_POLY derived from the part of thermal conductivity of the mixture
depending on porosity.
9.7.38 Operand EMMAG
Coefficient of storage. This coefficient is taken into account only in the cases of modeling
with mechanics.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
109/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
9.8
Key word factor SURF_ETAT_SATU (cf [R7.01.14])
9.8.1 Syntax
SURF_ETAT_SATU
:
_F (
E_CHAR
:
EC. [R]
E_DECHAR
:
Edc
[R]
XN
:
xn [R]
RF
:
RF [R]
EV_KB
:
evkb
[R]
EV_XM
:
evxm
[R]
D_E_T
:
det
[R]
ALPHA0
:
a0 [R]
ALPHA1
:
a1 [R]
ALPHA2
:
a2 [R]
ALPHA3
:
a3 [R]
ALPHA_S:
have [R]
ANG_FRT:
ang
[R]
COHE:
Co [R]
RESI_TRAC
:
rtrac [R]
)
9.8.2 Operand
E_CHAR
Coefficient of the load module.
Value recommended in unit IF between 50 and 500.
9.8.3 Operand
E_DECHAR
Coefficient of the module of unloading.
Value recommended in unit IF between 50 and 500.
9.8.4 Operand
EV_KB
Coefficient of the voluminal modulus of deformation.
Value recommended in unit IF between 100 and 1500.
9.8.5 Operand
RF
Coefficient of the hyperbolic law.
Value recommended in unit IF between 0,5 and 0,95.
9.8.6 Operand
XN
Exponent of the nonlinear law (Dependence of the module to containment).
Value recommended in unit IF between 0 and 1.
9.8.7 Operand
EV_XM
Exponent of the law of surface of state of the index of the vacuums.
Value recommended in unit IF between 0 and 1.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
110/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
9.8.8 Operand
D_E_T
Variation of the module D Young with the temperature.
Value recommended in unit IF between 1.E-4 and 1.E-5.
9.8.9 Operand
ANG_FRT
Angle of friction of the ground.
Value recommended between 0 and 0,25 degrees.
9.8.10 Operand COHE
Cohesion of the ground.
Value recommended in unit IF between 1 and 10 MPa.
9.8.11 Operand RESI_TRAC
Resistance in traction of the ground.
9.8.12 Operand ALPHA0
Constant for the dependence compared to the temperature of the surface of state of the index of the vacuums.
9.8.13 Operand ALPHA1
Constant for the dependence compared to the temperature of the surface of state of the index of the vacuums.
9.8.14 Operand ALPHA2
Constant for the dependence compared to the temperature of the surface of state of the index of the vacuums.
9.8.15 Operand ALPHA3
Constant for the dependence compared to the temperature of the surface of state of the index of the vacuums.
9.8.16 Operand ALPHA_S
Expansion factor of the solid matter constituents.
Value recommended in unit IF between 3.E-5 and 5.E-5.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
111/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
9.9
Key word factor SURF_ETAT_NSAT (cf [R7.01.14])
9.9.1 Syntax
SURF_ETAT_NSAT
:
_F (
E_CHAR
:
EC. [R]
E_DECHAR
:
Edc
[R]
XN
:
xn [R]
RF
:
RF [R]
EV_KB
:
evkb
[R]
EV_XM
:
evxm
[R]
EV_A:
eva
[R]
EV_B:
evb
[R]
EV_CT
:
evct
[R]
EV_SIGB:
evsb
[R]
D_E_T
:
det
[R]
D_E_SUCC
:
[R]
ANG_FRT:
ang
[R]
COHE:
cohe
[R]
D_COEH_SUCC:
DCS [R]
ANG_FRT_ULT:
afu [R]
SUCC_ULTM
:
known [R]
RESI_TRAC
:
rt [R]
A_SURF_SATU:
has
[R]
B_SURF_SATU:
B
[R]
C_SURF_SATU:
C
[R]
D_SURF_SATU:
D
[R]
)
9.9.2 Operand
E_CHAR
Coefficient of the load module.
Value recommended in unit IF between 50 and 500.
9.9.3 Operand
E_DECHAR
Coefficient of the module of unloading.
Value recommended in unit IF between 50 and 500.
9.9.4 Operand
RF
Coefficient of the hyperbolic law.
Value recommended in unit IF between 0,5 and 0,95.
9.9.5 Operand
XN
Exponent of the nonlinear law (Dependence of the module to containment).
Value recommended in unit IF between 0 and 1.
9.9.6 Operand EV_KB
Coefficient of the voluminal modulus of deformation.
Value recommended in unit IF between 100 and 1500.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
112/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
9.9.7 Operand
EV_XM
Exponent of the law of surface of state of the index of the vacuums.
Value recommended in unit IF between 0 and 1.
9.9.8 Operand
EV_A
Coefficient has surface D index of the vacuums.
9.9.9 Operand EV_B
Coefficient B of surface D index of the vacuums.
9.9.10 Operand EV_CT
Coefficient C of surface D index of the vacuums.
9.9.11 Operand EV_SIGB
Coefficient sigma of surface D index of the vacuums.
9.9.12 Operand D_E_T
Variation of the module D Young with the temperature.
Value recommended in unit IF between 1.E-4 and 1.E-5.
9.9.13 Operand D_E_SUCC
Variation of the module D Young with suction.
9.9.14 Operand ANG_FRT
Angle of friction of the ground.
Value recommended between 0 and 0,25 degrees.
9.9.15 Operand ANG_FRT_ULT
Ultimate angle of friction.
9.9.16 Operand COHE
Cohesion of the ground.
Value recommended in unit IF between 1 and 10 MPa.
9.9.17 Operand D_COEH_SUCC
Variation of cohesion with suction.
9.9.18 Operand RESI_TRAC
Resistance in traction of the ground.
9.9.19 Operand SUCC_ULTM
Ultimate suction.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
113/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
9.9.20 Operand A_SURF_SATU
Coefficient has surface of state of saturation.
9.9.21 Operand B_SURF_SATU
Coefficient B of the surface of state of saturation.
9.9.22 Operand C_SURF_SATU
Coefficient C of the surface of state of saturation.
9.9.23 Operand D_SURF_SATU
Coefficient D of the surface of state of saturation.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
114/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
9.10 Key word factor CAM_CLAY_THM (cf [R7.01.14])
9.10.1 Syntax
CAM_CLAY_THM
: _F (
NAKED
:
naked [R]
LAMBDA
:
lambda
[R]
KAPA:
kapa
[R]
M:
m
[R]
PRES_CRIT
:
PC [R]
GAMMA:
gamma
[R]
A0_PC
:
a0 [R]
A1_PC
:
a1 [R]
A2_PC
:
a2 [R]
ALPHA0_PC
:
al0
[R]
ALPHA1_PC
:
al1
[R]
ALPHA2_PC
:
al2
[R]
ALPHA3_PC
:
al3
[R]
ALPHA_S:
als
[R]
)
9.10.2 Operand NAKED
Poisson's ratio.
9.10.3 Operand LAMBDA
Slope of the straight line of loading.
Value recommended in unit IF between 0.1 and 0.4.
9.10.4 Operand KAPA
Slope of the straight line of unloading.
Value recommended in unit IF between 0.01 and 1.
9.10.5 Operand PRES_CRIT
Effective critical pressure.
9.10.6 Operand M
Slope of the critical line of state.
Value recommended in unit IF between 0.8 and 0.9.
9.10.7 Operand GAMMA
Ecs 1
Ecs being the index of the vacuums for 1 MPa of containment.
The value recommended for Ecs in unit IF is between 1 and 3.
9.10.8 Operand A0_PC
Coefficient of definition of the stress of preconsolidation PC of the surface of load.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
115/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
9.10.9 Operand A1_PC
Coefficient of definition of the stress of preconsolidation PC of the surface of load.
9.10.10 Operand A2_PC
Coefficient of definition of the stress of preconsolidation PC of the surface of load.
9.10.11 Operand ALPHA0_PC
Coefficient of definition of the stress of preconsolidation PC of the surface of load.
9.10.12 Operand ALPHA1_PC
Coefficient of definition of the stress of preconsolidation PC of the surface of load.
9.10.13 Operand ALPHA2_PC
Coefficient of definition of the stress of preconsolidation PC of the surface of load.
9.10.14 Operand ALPHA3_PC
Coefficient of definition of the stress of preconsolidation PC of the surface of load.
9.10.15 Operand ALPHA_S
Expansion factor of the solid matter constituents.
Value recommended in unit IF between 3.e-5 and 5.e-5.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
116/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
9.11 Word
key
CAM_CLAY
The Camwood-Clay model is an elastoplastic model used in soil mechanics and is
especially adapted to argillaceous materials. The model presented here is called modified Camwood-Clay.
document [R7.01.14] described the corresponding equations. This model can be used
independently of behaviors THM. The elastic characteristics must be defined under
key word ELAS.
9.11.1 Syntax
CAM_CLAY = _F
(
LAMBDA
=
lambda
,
[R]
KAPA =
kapa,
[R]
M
=
m
,
[R]
PORO =
poro,
[R]
PRES_CRIT
= prescr
, [R]
AP
=
AP
,
[R]
)
9.11.2 Operands LAMBDA
Coefficient of compressibility (plastic slope in a hydrostatic test of compression).
9.11.3 Operands KAPA
Elastic coefficient of swelling (elastic slope in a hydrostatic test of compression).
9.11.4 Operands M
Critical line slope of state.
9.11.5 Operands PORO
Initial porosity. If CAM_CLAY is used under RELATION_KIT, key word PORO indicated under
CAM_CLAY and under THM_INIT must be the same one.
9.11.6 Operands PRES_CRIT
The critical pressure equalizes with half of the pressure of consolidation.
9.11.7 Operands AP
Initial pressure corresponding to initial porosity generally equal to the atmospheric pressure.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
117/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
9.12 Key word factor CJS
The law (Cambou, Jaffani, Sidoroff) is a law of behavior for the grounds. It comprises three
mechanisms, one corresponds to nonlinear elasticity, another corresponds to a plasticization
for isotropic states of stresses, and the third mechanism corresponds to a dependant plasticization
in a state of stress déviatoire. The document [R7.01.13] described with precision the equations
corresponding.
The elastic characteristics must be defined under key word ELAS.
Law CJS covers three possible forms (CJS1, CJS2 and CJS3), according to whether one authorizes or not
the activation of the nonlinear mechanisms.
Table Ci below gives the mechanisms activated for three levels CJS1, CJS2 and CJS3:
Elastic mechanism isotropic plastic Mechanism
Plastic mechanism
déviatoire
CJS1
linear
not activated
activated, perfect plasticity
CJS2
nonlinear
activated
activated, isotropic work hardening
CJS3
nonlinear
activated
activated, kinematic work hardening
Note:
By adopting the correspondence of the parameters for the limiting states, it is possible to use
behavior CJS1 to modelize a law of Mohr Coulomb in soil mechanics.
9.12.1 Syntax
CJS = _F (
BETA_CJS = beta,
[R]
RM
=
rm,
[R]
N_CJS
=
N
,
[R]
KP
=
kp,
[R]
RC
=
rc,
[R]
A_CJS
=
has
,
[R]
B_CJS
=
B
,
[R]
C_CJS
=
C
,
[R]
GAMMA_CJS
=
G
,
[R]
MU_CJS
=
driven,
[R]
PCO
=
pco
,
[R]
AP
=
AP,
[R]
Q_INIT
=
Q
,
[R]
R_INIT
=
R
,
[R]
)

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
118/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
The various coefficients are to be informed or not according to the level which one wants to use,
in accordance with table Ci below (F for optional, O for obligatory and nothing for without object).
Symbol
Q init
_
R init
_
N
K
p
R
C
With
Key word
Q_INIT R_INIT N_CJS
KP GAMMA_CJS BETA_CJS RC
A_CJS
CJS1 F O O
CJS2 F F O
O O O O O
CJS3 F O
O O O O
Symbol
B
R
m
µ
p
Co
C
P
has
Key word
B_CJS RM M_CJS
PCO C_CJS AP
CJS1 O
O
CJS2 O
O
CJS3 O O O O O
O
We draw the attention of the user to the fact that, for the same material, the same coefficient
can take different values according to the level used. The level used is never indicated, it
is indicated by the fact that certain coefficients are indicated or not.
In addition, key word ELAS must be obligatorily indicated when one uses law CJS (under one of
its three levels). The definition of the Young modulus and the Poisson's ratio make it possible to calculate
coefficients
K
oe
and
G
O
.
9.12.2 Operand BETA_CJS
For levels CJS1, CJS2 CJS3.
Parameter
. Control the plastic variation of volume in the mechanism déviatoire.
9.12.3 Operand RM
For levels CJS1, CJS2 CJS3.
Maximum value of opening of the field of reversibility déviatoire.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
119/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
9.12.4 Operand N_CJS
For levels CJS2 CJS3.
Control the dependence of the modulus of elasticity with the mean stress.
K
K
I
Q
P
oe
init
has
N
=
+
1
3
G G
I
Q
P
O
init
has
N
=
+
1
3
9.12.5 Operand KP
For levels CJS2 CJS3.
Modulate plastic compressibility.
&
&
&
Q
K Q
K
Q
P
Q
Iso
p
COp
Iso
has
N
=
=
9.12.6 Operand RC
For levels CJS2 CJS3
Value criticizes variable R:
&
&
vdp
II
II
C
ij
ij
dp
II
S
S
S.E.
S
= -
-
1
()
S
R I
H
II
C
C
S
= -
1
9.12.7 Operand A_CJS
For levels CJS2.
Control the isotropic work hardening of the mechanism déviatoire;
R
WITH R R
R
With R
m
m
=
+
9.12.8 Operand R_INIT
For levels CJS2.
Initial value of the variable
R
. At the first calculating time, if the initial value of
R
is null, that is to say
that one did not define an initial state of the internal variables by key word ETAT_INIT of STAT_NON_LINE,
either that this initial state or no one, one will take as initial value that definite by key word R_INIT of
DEFI_MATERIAU.
9.12.9 Operand B_CJS
For levels CJS3.
Control the kinematic work hardening of the mechanism déviatoire;
&
&
.
X
B
Dev.
F
X
I
X
I
P
ij
D
D
ij
ij
has
= -
-
-
1
3
1
1
1 5

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
120/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
9.12.10 Operand C_CJS
For levels CJS3.
Control the evolution of the critical pressure
(
)
p
p
C
C
Co
v
=
-
exp
.
9.12.11 Operand PCO
For levels CJS3.
initial critical pressure
(
)
p
p
C
C
Co
v
=
-
exp
.
9.12.12 Operand GAMMA_CJS
For levels CJS1 CJS2 CJS3.
Control the form of the criterion:
()
()
(
)
()
H
S
S
S
S
II
= +
=
+
1
3
1
54
1 6
3
1 6
cos
det
/
/
9.12.13 Operand MU_CJS
For levels CJS3.
Control the value of rupture of variable R.
R
R
p
I
R
C
C
=
+
µ
ln 3
1
9.12.14 Operand AP
For levels CJS1 CJS2 CJS3.
atmospheric pressure. Must be given negative.
9.12.15 Operand Q_INIT
For levels CJS1 CJS2 CJS3.
Numerical parameter allowing to make acceptable a null state of stress. Can also be
used to define a cohesion, at least for level CJS1. The formula will be used:
Q
C
init
= - 3 cotan
.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
121/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
9.13 Key word factor LAIGLE
The law of LAIGLE [R7.01.15] is a rheological model of behavior for the modeling of
rocks. Those are characterized by the three following parameters:
·
“has” which defines the influence of the component of dilatancy in the behavior in large
deformations. This parameter depends on the level of deterioration of the rock,
·
“S” which defines the cohesion of the medium. It is thus representative of the damage of
rock,
·
“m” is a function of the mineralogical nature of the rock, and is associated a return
of experiment important.
The elastic characteristics must be definite soue key word ELAS.
9.13.1 Syntax
LAIGLE =_F (
GAMMA_ULT
= gamma_ult,
[R]
GAMMA_E =
gamma_e,
[R]
M_ULT
=
m_ult
,
[R]
M_E
=
m_e
,
[R]
A_E
=
a_e
,
[R]
M_PIC
=
m_pic,
[R]
A_PIC
=
a_pic,
[R]
ETA
=
eta
,
[R]
SIGMA_C =
sigma_c,
[R]
GAMMA
=
gamma,
[R]
KSI
=
ksi
,
[R]
GAMMA_CJS
=
gamma_cjs, [R]
SIGMA_P1
=
sigma_p1,
[R]
AP
=
AP
,
[R]
)
9.13.2 Operand GAMMA_ULT
Parameter
ult
: Plastic deformation déviatoire corresponding to the bearing.
9.13.3 Operand GAMMA_E
Parameter
E
: Plastic deformation déviatoire corresponding to the complete disappearance of
cohesion.
9.13.4 Operand M_ULT
Parameter
m
ult
: Value of
m
ultimate criterion reached
ult
.
9.13.5 Operand M_E
Parameter
m
E
: Value of
m
intermediate criterion reached in
E
.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
122/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
9.13.6 Operand A_E
Parameter
E
has
: Value of
has
intermediate criterion reached in
E
.
9.13.7 Operand M_PIC
Parameter
peak
m
: Value of
m
criterion of peak reached with the peak of stress.
9.13.8 Operand A_PIC
Parameter
peak
has
: Value of the exponent
has
with the peak of stress.
9.13.9 ETA operand
Parameter
: Exponent controlling work hardening.
9.13.10 Operand SIGMA_C
Parameter
C
: Resistance in simple compression.
9.13.11 Operands GAMMA and KSI
Parameters
and
: Parameters regulating dilatancy.
A condition to respect is that the report/ratio
remain lower than 1. In the case of hard stones very
resistant, subjected to stresses of containment relatively low, the variation of
dilatancy
sin
(according to the state of the stresses - to see [R7.01.15]) can tend towards
, which
justify this condition.
9.13.12 Operand GAMMA_CJS
Parameter
cjs
: Parameter of form of the surface of load in the déviatoire plan.
9.13.13 Operand SIGMA_P1
Parameter
1
p
: Intersection of the intermediate criterion and the criterion of peak.
9.13.14 Operand AP
Atmospheric pressure. Must be given positive.
Note:
Parameters M_E, A_E, A_PIC, SIGMA_P1, SIGMA_C and MPIC are dependant the ones
others by the relation:
E
peak
has
has
C
p
peak
p
C
E
m
m
+
=
1
1
1
. This dependence is checked with the center
code.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
123/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
9.14 Key word factor DRUCKER_PRAGER
The law of DRUCKER_PRAGER [R7.01.16] is a model of behavior for the mechanics of
grounds, it is defined by the relation:
0
)
(
1
-
+
p
R
I
eq
where
eq
is a function of the diverter of the effective stresses
,
()
= Tr
I
1
is the trace of the effective stresses,
is a coefficient of dependence in pressure,
)
(p
R
is a function of the cumulated plastic deformation.
In the linear case, the function
R
is given by:
+
=
+
=
<
<
y
ult
ult
y
ult
p
H
)
p
(
R
p
p
p
H
)
p
(
R
p
p
0
In the parabolic case,
()
p
F
)
p
(
R
y
=
where the function
()
p
F
is given by
:
()
()
=
-
-
=
<
<
y
ult
y
ult
2
ult
y
ult
y
ult
p
F
p
p
p
p
1
1
p
F
p
p
0
9.14.1 Syntax
DRUCKER_PRAGER =_F
(
WORK HARDENING =/
`LINEAR `
,
/`PARABOLIC `,
ALPHA
=
alpha,
[R]
P_ULTM
=
p_ult
,
[R]
SY
=
sy
,
[R]
H
=
H,
[R]
SY_ULTM =
sy_ult, [R]
)
9.14.2 Operand WORK HARDENING
Allows to define the type of desired work hardening.
9.14.3 Operand ALPHA
Indicate the coefficient of dependence in pressure. It is reminded the meeting that the operand ALPHA is connected to
the angle of friction
by the relation:
)
sin (
3
)
sin (
.
2
-
=
.
9.14.4 Operand P_ULTM
Indicate the ultimate cumulated plastic deformation.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
124/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
9.14.5 Operand SY
Indicate the plastic stress. This operand is related to the combination of the binding fraction
C
with the angle of friction
in the following way:
)
sin (
3
)
cos (
C
6
SY
-
=
.
9.14.6 Operand H
Indicate the module of work hardening, H < 0 if the law is lenitive. This operand is obligatory for
work hardening of a linear type (operand WORK HARDENING = `LINEAR `).
9.14.7 Operand SY_ULTM
Indicate the ultimate stress. This operand is obligatory for work hardening of a parabolic type
(operand WORK HARDENING = `PARABOLIC `).
9.15 Key word BARCELONA factor
The model of Barcelona describes the elastoplastic behavior of the unsaturated grounds coupled with
hydraulic behavior (cf [R7.01.14] for more detail). This model is reduced to the model
Cam_Clay in the saturated case. Two criteria intervene: a mechanical criterion of plasticity (that
of Cam_Clay) and a hydrous criterion controlled by suction (or capillary pressure). It cannot be
used that within the framework of behaviors THHM and HHM. Characteristics necessary to
model must be given under this key word and the key words
CAM_CLAY
and
ELAS
.
It is thus obligatory to inform the parameters of key words CAM_CLAY and ELAS.
9.15.1 Syntax
BARCELONA = _F
(
R
=
R
,
[R]
BETA =
beta,
[R]
KC
=
kc
,
[R]
PC0_INIT = Pc0 (0)
, [R]
KAPAS
=
Kappas
,
[R]
LAMBDAS =
Lambdas,
[R]
ALPHAB
=
alphab, [R]
)
9.15.2 Operands R, BETA
Adimensional coefficients intervening in the expression:
() () (
)
[
]
R
p
R
p
C
C
+
-
-
=
)
exp (
1
0
9.15.3 Operand KC
Adimensional parameter controlling the increase in cohesion with suction (pressure
thin cable).
9.15.4 Operand PCO_INIT
Initial threshold of the capillary pressure (homogeneous with stresses).
9.15.5 Operand KAPAS
Adimensional coefficient of rigidity associated the change of suction in the elastic range.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
125/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
9.15.6 Operand LAMBDAS
Coefficient of compressibility related to a variation of suction in the plastic range.
(adimensional).
9.15.7 Operand ALPHAB
Coefficient of correction of the normality of the plastic flow [R7.01.17].
Optional and adimensional corrective term allowing to better take into account results
experimental. By defect, it is calculated by Code_Aster according to the slope of the straight line of state
critical, of the coefficient of swelling and the coefficient of compressibility.
9.16 Key word factor HOEK_BROWN
Law of behavior in rock mechanics of the law type of modified HOEK-BROWN (cf.
[R7.01.18]
Mechanical characteristics elastic E, NAKED, and ALPHA must be defined in parallel under
key word ELAS.
9.16.1 Syntax
HOEK_BROWN = _F (
GAMMA_RUP
=
grup,
[R]
GAMMA_RES
=
likings,
[R]
S_END
=
send,
[R]
S_RUP
=
srup,
[R]
M_END
=
mend,
[R]
M_RUP
=
mrup,
[R]
BETA =
beta,
[R]
ALPHAHB = alphahb, [R]
PHI_RUP =
prup,
[R]
PHI_RES =
near,
[R]
PHI_END =
phiend, [R]
)
9.16.2 Operand GAMMA_RUP
Value of the parameter of work hardening to the rupture of material.
9.16.3 Operand GAMMA_RES
Value of the parameter of work hardening at the beginning of residual resistance.
9.16.4 Opérande_S_END
Value of the product S * SIGMA_c ** 2 attack with the initiation of damage.
9.16.5 Operand S_RUP
Value of the product S * SIGMA_c ** 2 attack in GAMMA_RUP.
9.16.6 Operand M_END
Value of the product M * SIGMA_c reached with the initiation of damage.
9.16.7 Operand M_RUP
Value of the product M * SIGMA_c reached in GAMMA_RUP.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
126/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
9.16.8 Operand BETA
Parameter characterizing the behavior post-rupture of material.
9.16.9 Operand ALPHAB
Parameter characterizing the behavior post-rupture of material.
9.16.10 Operand PHI_RUP
Value of the angle of friction reached in GAMMA_RUP.
9.16.11 Operand PHI_RES
Value of the angle of friction reached in GAMMA_RÉS.
9.16.12 Operand PHI_END
Value of the angle of friction to the initiation of damage (taken null by defect).

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
127/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
10 Behaviors specific to the elements 1D
10.1 Key words factor
VMIS_POUTRE
/
VMIS_POUTRE_FO
Parameters defining the total criterion of plasticity intervening in the elastoplastic behavior
elements of beam (Modelings
POU_D_E
,
POU_D_T
,
POU_D_TG
). (See [R5.03.30]).
The criterion of plasticity is defined by:
(
) (
)
()
G
p
F
R p
T Q
T Q
p
p
,
,
,
=
-
0
with
(
)
()
()
F
NR
NR
NR
With
M
With
M
M
M
p
p
y
YP
y
Z
zp
Z
px
X
T Q
p
,
.
.
=
+
+
+
2
2
2
2
2
2
()
p
R
can be calculated starting from ECRO_FLEJOU or ECRO_LINE.
With regard to the bending, the functions
()
With
y
YP
and
()
With
Z
zp
allow the progressive passage of
moment of beginning of plasticization of the section (in general,
M
I
Z
ey
y y
=
max
and
M
I
y
ez
Z y
=
max
) with
limiting moment
M
M
py
ey
=
(
M
M
pz
ez
=
). These moments are to be introduced directly by
the user, they are not calculated by the code according to the elastic limit
y
and of
geometry of the section. The value of
depends on the form of the section: conventional values
are:
·
1.5 for a rectangular section
·
4
for a hollow circular section
·
16
3
for a full circular section.
Functions
()
With
y
YP
and
()
With
Z
zp
are defined by the preceding characteristic moments, and them
numerical parameters
y
y
Z
Z
:
()
()
()
()
With
M
M
With
y
YP
YP
py
y
ey
YP
y
Z
zp
y
y
=
+
+
=
2
2
......
The normal effort limits is characterized by
NR
S
p
y
=
. The limiting torque is
M
C
px
y
=
.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
128/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
10.1.1 Syntax
/VMIS_POUTRE
/
VMIS_POUTRE_FO = _F (
NP
=Np
,
[R
] or [
function **]
MEY
=Mey,
[R
] or [
function **]
MPY
=
Mpy
,
[R
] or [
function **]
CAY
=
ay,
[R
] or [
function **]
CBY
=
by,
[R
] or [
function **]
MEZ
=
Mez
,
[R
] or [
function **]
MPZ
=
Mpz
,
[R
] or [
function **]
CAZ
=
az,
[R
] or [
function **]
CBZ
=
bz,
[R
] or [
function **]
MPX
=
Mpx
,
[R
] or [
function **]
)
10.2 Key word factor
ECRO_FLEJOU
Definition of the curve of work hardening
()
R p
:
R p
S
S
H p
p
E
L
y
p
U
U
U
y
p
()
.
=
=
+
+
=
-
1
1
with
that is to say
It is thus necessary to respect
H
E E
E E
E
E H
E H
E
E
p
p
p
p
=
-
=
+
<
.
.
This curve has the advantage of presenting a horizontal asymptote equalizes with
U
(cf [R5.03.30]).
10.2.1 Syntax
ECRO_FLEJOU = _F (
EP = ep,
[R]
SY = sy,
[R]
KNOWN = known,
[R]
THEN =
alpha
,
[R]
)

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
129/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
10.3 Key word factor
ECRO_ASYM_LINE
(cf [R5.03.09])
It makes it possible to modelize a behavior with linear isotropic work hardening, but with limits
of elasticity and different modules of work hardening in traction and compression. This is used by
the model of behavior 1D VMIS_ASYM_LINE, usable for elements of bar.
Elastic behavior in traction and compression is the same one: even Young modulus.
There are two fields of isotropic work hardening defined by R
T
and R
C.
The two fields are
independent one of the other. We adopt an index T for traction and C for compression.
YT
Effort limits in traction. In absolute value.
TESTSTEMYÇ
Effort limits in compression. In absolute value.
p
T
Plastic deformation cumulated in traction. Algebraic value.
p
C
Plastic deformation cumulated in compression. Value
algebraic.
E
TT
Slope of work hardening in traction.
E
TC
Slope D `work hardening in compression.
The equations of the model of behavior are:
()
()
()
()
()
()
&
&
&
&
&
&
&
&
&
&
&
&
&
&
p
HT
p
C
p
T
p
C
p
C
T
p
T
T
T
C
C
C
C
C
C
C
C
T
T
T
T
T
T
p
p
R p
R p
p
R p
p
R p
p
R p
p
R p
= -
-
=
+
=
=
-
- -
=
- -
<
- =
=
-
<
=
-
·
1
0
0
0
0
0
0
0
0
678
with
if
if
if
if
where:
&
CP
: speed of plastic deformation in compression,
&
Tp
: speed of plastic deformation in traction
HT
: thermal deformation of origin:
(
)
HT
ref.
T T
=
-
.
is defined under ELAS.
It is noticed that one cannot have simultaneously plasticization in traction and compression: that is to say
&p
C
= 0
, that is to say
&p
T
= 0
, that is to say both are null.
10.3.1 Syntax
ECRO_ASYM_LINE = _F (
DT_SIGM_EPSI
= RT,
SY_T =
yT,
DC_SIGM_EPSI = RC,
SY_C =
teststemyç,

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
130/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
11 Behaviors
private individuals
11.1 Key word factor LEMAITRE_IRRA
Characteristics (specific to the irradiation) of the creep of the pencils or fuel assemblies
(behavior LEMAITRE_IRRA of STAT_NON_LINE).
The elastic characteristics must be defined under key word ELAS or ELAS_FO.
The uniaxial form of the law of growth is:
() (
)
S
T
G
D
B
At
T
+
=
0
.
where
is the neutron flux and
T
D
0
fluence, recovered in STAT_NON_LINE by the key word
IRRA of VARI_COMM.
T
is in °C.
If one adopts a modeling 1D (the behavior is then applied to an element of
beam in the axial direction, cf [R5.03.09]), this uniaxial form is used just as it is.
On the other hand, for modelings 2D and 3D, the law of growth is written (cf [R5.03.08]):
() (
)
1
0
0
0
0
0
0
0
0
1
:
.
0
0
0
R
G
G
S
T
G
D
B
At
T
=
+
=
with
One must then define using operand ANGLE_REP of the MASSIVE key word of the operator
AFFE_CARA_ELEM local axes corresponding to the reference mark
R
1
(see [U4.42.01]). This operand
awaits 3 nautical angles of which one uses only the 2 first (the third can thus be
unspecified).
The parameters of growths are provided behind key words GRAN_A, GRAN_B and GRAN_S.
One informs four key words QSR_K, BETA, PHI_ZERO, L (the other parameters of creep are
identical to those of behavior LEMAITRE) and behavior in creep is then according to:
(
)
(
)
&
/
p
p
K
L
E
T
eq
Q
R T T
m
N
=
+
=
-
+
°
1
1
0
0
0
273,15 C
where
is the neutron flow calculated starting from the fluence recovered in STAT_NON_LINE by
operand IRRA of key word VARI_COMM (see [R5.03.08] or [R5.03.09] according to modeling).
T
is
in °C.
If it is wished that the behavior not depend on the fluence, but comprises
nevertheless the term in exp (- Q/RT), it is possible, only for modelings 2D and 3D,
to use key word LEMAITRE_IRRA in STAT_NON_LINE by informing key word LEMAITRE
_IRRA in DEFI_MATERIAU. It is then necessary imperatively to affect UN_SUR_K, A, B, S with zero and
PHI_ZERO with one. Under these conditions, it is not necessary to define a field of fluence.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
131/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
11.1.1 Syntax
LEMAITRE_IRRA
= _F
(
NR
=
N,
[R]
UN_SUR_K
= 1/K
, [R]
UN_SUR_M
=/1/m
, [R]
/
0.
,
[DEFECT]
QSR_K =/Q/R
, [R]
/
0.
,
[DEFECT]
BETA =/
, [R]
/
0.
,
[DEFECT]
PHI_ZERO =/
0,
[R]
/
0.
,
[DEFECT]
L =/L, [R]
/
0.
,
[DEFECT]
GRAN_A
=/has, [R]
/
0.
,
[DEFECT]
GRAN_B
=/B, [R]
/
0.
,
[DEFECT]
GRAN_S
=/S, [R]
/
0.
,
[DEFECT]
)
11.2 Key word factor
LMARC_IRRA
Élasto-viscoplastic model developed with the LMA-RC to describe the viscoplastic behavior
orthotropic of the tubes of sheaths of the fuel pin [R5.03.10], supplemented by the parameters of
growth provided behind key words GRAN_A, GRAN_B and GRAN_S.
Briefly, the relations of behavior are:
(
)
(
)
(
)
()
()
()
(
)
()
F
X
X M
X
F
M
X
X
M
X
X
NR
Q X X
X
X
X
X
=
-
-
=
-
-
=
=
-
-
=
=
-
=
-
-
-
-
~
~
~
&
&v
&v
~
~
&v
&
&
& sin
~
&
v
&
&v
sinh
v
v
v
v
R
H
K
p
Y
R
X
NR R
T
p
p T
p
N
p
m
m
0
1
0
1
0
1
3
2
3
2
2
3
2
3
()
()
()
(
)
()
()
()
=
-
-
=
-
p
Y
p
Y
p
p
1
1
2
2
2
2
2
3
2
3
v
&
&v
v
&
&v
v
v
NR
Q X
X
X
NR
Q X
with:
()
(
)
Y
Y
Y
Y
E
NR
B
T
v
v
=
+
-
=
0
3
2
X
X
X
Note:
~
represent the diverter of the stresses and
~
- X
the equivalent within the meaning of Hill.
Matrices
MR. NR R
Q
,
and
allow to describe the anisotropy of behavior
viscoplastic.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
132/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
11.2.1 Syntax
|
LMARC = = _F (
R_0
=
R0,
[R]
DE_0 =
eps
0,
[R]
NR
=
N
,
[R]
K
=
K
,
[R]
Y_0
=
y0
,
[R]
Y_I
=
yinfi,
[R]
B
=
B
, [R]
A_0
=
X0,
[R]
RM
=
rm,
[R]
M
=
m
, [R]
P
=
p
, [R]
P1
=
p1,
[R]
P2
=
p2,
[R]
M11
=
M11,
[R]
M22
=
M22,
[R]
M33
=
M33,
[R]
M66
=
M66,
[R]
N11
=
N11,
[R]
N22
=
M22,
[R]
N33
=
N33,
[R]
N66
=
N66,
[R]
Q11
=
Q11,
[R]
Q22
=
Q22,
[R]
Q33
=
Q33,
[R]
Q66
=
Q66,
[R]
R11
=
R11,
[R]
R22
=
R22,
[R]
R33
=
R33,
[R]
R66
=
R66,
[R]
GRAN_A
=/has,
[R]
/
0.
,
[DEFECT]
GRAN_B
=/B,
[R]
/
0.
, [DEFECT]
GRAN_S
=/S,
[R]
/
0.
, [DEFECT]
)
11.3 Key word factor
DIS_GRICRA
This key word makes it possible to define the parameters associated with the nonlinear behavior with the connection enters
the grid and the pencil in a fuel assembly modelized by a discrete element
(cf [R5.03.17]). The behavior usable in the controls
STAT_NON_LINE
and
DYNA_NON_LINE
starting from these parameters is DIS_GRICRA:
·
behavior being pressed on a discrete element with 2 nodes (modeling
DIS_TR
) with
degrees of freedom in translation and rotation
·
contact with friction of Coulomb for the degrees of translation, modelized by a model
elastoplastic
·
nonlinear law of behavior in rotation based on geometrical considerations and
physics (cf [R5.03.17])
A certain number of parameters additional, available for this behavior but which
do not appear in this document, are clarified in [V6.04.131].

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
133/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
11.3.1 Syntax
DIS_GRICRA =
_F (
% Behavior “DIS_GRICRA”
KN_BOS
=
/
kn_bossette,
[R]
KT_BOS
=/kt_bossette, [R]
KN_RES
=
/
kn_ressort,
[R]
KT_RES
=/kt_ressort, [R]
COUL_BOS
=/mu_bossette, [R]
COUL_RES
=
/
mu_ressort,
[R]
ECRO_BOS
=/gamma_bossette, [R]
ECRO_RES
=/gamma_ressort, [R]
FORC_SER
=/forc_serrage,
[R]
DIST_BOS
=/distance_bossette, [R]
)
11.3.2 Operands
The connection grid-pencil of the fuel assemblies consists of a system of bosses and of
springs (cf [R5.03.17]), for which one must specify the following parameters:
KN_BOS = kn_bossette
Normal rigidity of the bosses (in NR/m).
KT_BOS = kt_bossette
Tangential rigidity of the bosses (in NR/m).
KN_RES = kn_ressort
Normal rigidity of the springs (in NR/m).
KT_RES = kt_ressort
Tangential rigidity of the springs (in NR/m).
COUL_BOS = mu_bossette
Coefficient of Coulomb for the friction of the bosses.
COUL_RES = mu_ressort
Coefficient of Coulomb for the friction of the springs.
ECRO_BOS = gamma_bossette
Parameter of work hardening allowing to treat the friction of the bosses (in NR/m).
This parameter does not have a physical direction, and is introduced only to help the convergence of calculation
when there is slip (idem perfect plasticity).

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
134/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
ECRO_RES = gamma_ressort
Parameter of work hardening allowing to treat the friction of the springs (in NR/m)
This parameter does not have a physical direction, and is introduced only to help the convergence of calculation
when there is slip (idem perfect plasticity).
FORC_SER = forc_serrage
Force tightening (positive) initial pencil in the grid (equal to the force applied to the springs)
(in NR).
DIST_BOS = distance_bossette
Outdistance between the bosses (in m).
This parameter must be readjusted if one uses only one discrete to modelize several connections
grid-pencil, and thus does not correspond necessarily to the true distance between the bosses
measured on the grids of the assembly.
11.4 Key word factor
GATT_MONERIE
Thermomechanical law of behavior of fuel “GATT-Monerie” in order to simulate tests
of indentation. This law of behavior is an isotropic élasto-viscoplastic law without work hardening
whose specifities are:
· the potential of dissipation is the sum of two potentials of the Norton type (without threshold),
· the fuel having a residual porosity likely to evolve/move in compression
(thickening), this potential depends, in addition to the equivalent stress, of the stress
hydrostatic.
The two internal variables of this model are the plastiquecumulée deformation and the fraction
voluminal of porosity.
11.4.1 Syntax
GATT_MONERIE
= _F
(
D_GRAIN =
/
d_grain,
[R]
PORO_INIT
=/poro_init
, [R]
EPSI_01 =
/
eps1,
[R]
/
2.7252E-10,
[DEFECT]
EPSI_02 =
/
eps2,
[R]
/
9.1440E-41
[DEFECT]
with
D_GRAIN
:
cut combustible grain
PORO_INIT:
initial porosity
EPSI_01:
coefficient speed of forced low deformation
EPSI_02:
coefficient speed of forced strong deformation
The elastic characteristics must be indicated under key word ELAS.
11.5 Key word factor
DIS_CONTACT
This key word makes it possible to define the parameters associated with the nonlinear behaviors with contact or
shock with friction associated with the discrete elements (cf [R5.03.17]). Behaviors usable
in the controls
STAT_NON_LINE
and
DYNA_NON_LINE
starting from these parameters are:
·
DIS_CONTACT
: behavior being pressed on a discrete element with 2 nodes (modelings
DIS_T
and
DIS_TR
):
1) contact with friction of Coulomb for the degrees of translation,
2) relation of behavior of the elastoplastic type for the degrees of rotation
·
DIS_CHOC
: shock with friction of Coulomb being pressed on a discrete element with 1 or 2
nodes (modelings
DIS_T
or
DIS_TR
being pressed on meshs
POI1
or SEG2).

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
135/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
11.5.1 Syntax
DIS_CONTACT =
_F (
% Behavior “DIS_CHOC”
RIGI_NOR
=
KN,
[R]
DIST_1 =/dist1,
[R]
/
0,
[DEFECT]
DIST_2 =/dist2,
[R]
/
0,
[DEFECT]
RIGI_TAN
=/Kt,
[R]
/
0,
[DEFECT]
AMOR_NOR
=/Cn,
[R]
/
0,
[DEFECT]
AMOR_TAN
=/Ct,
[R]
/
0,
[DEFECT]
COULOMB
=/driven,
[R]
/
0,
[DEFECT]
PLAY
=
/
d0,
[R]
/
0,
[DEFECT]
% Behavior “DIS_CONTACT”
COULOMB
=/driven,
[R]
/
0,
[DEFECT]
KT_ULTM
=/ktu
, [R]
/
0,
[DEFECT]
EFFO_N_INIT =
Finished
,
[R]
/
RIGI_N_FO
= Fn, (T)
[fonction+]
/
RIGI_N_IRRA=FF, (fluence) [function]
/RELA_MZ
= f_mz,
[function]
/
ANGLE_1
=
a1,
[function]
ANGLE_2
=
a2,
[function]
ANGLE_3
=
a3,
[function]
ANGLE_4
=
a4,
[function]
MOMENT_1 =
m1,
[function]
MOMENT_2 =
m2,
[function]
MOMENT_3 =
m3,
[function]
MOMENT_4 =
m4,
[function]
C_PRAGER_MZ =/Cpr
, [R]
/
0,
[DEFECT]
)

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
136/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
11.5.2 Operands
Behavior
“DIS_CONTACT”
:
Behavior concerning the degrees of freedom of translation
COULOMB = driven
Value of the coefficient of friction.
EFFO_N_INIT = Finished
Initial normal effort in the spring (in general negative, so that there is contact at the initial moment).
KT_ULTM = ktu
Slope of regularization which simulates a nonperfect slip.
RIGI_N_FO = Fn (T)
Multiplying function (depend on time) of rigidity, in general decreasing with time,
to simulate the effect of the irradiation on the rigidity of the spring.
RIGI_N_IRRA = FF (fluence)
Multiplying function (depend on the fluence) of rigidity, in general decreasing with
fluence, to simulate the effect of the irradiation on the rigidity of the spring. To define this function, it is necessary
to use the control
DEFI_FONCTION
and to take for example as
NOM_PARA
,
“INST”
: for
the moment the fluence does not form part of
NOM_PARA
possible.
Behavior concerning the degrees of freedom of rotation
RELA_MZ = f_mz
Curve
(moment) according to DR. (degree of rotation)
ANGLE_1 = a1, MOMENT_1 = m1,
ANGLE_2 = a2, MOMENT_2 = m2,
ANGLE_3 = a3, MOMENT_3 = m3,
ANGLE_4 = a4, MOMENT_4 = m4,
Definition of the curve moment-angle of the characteristic in rotation of the connection grid-pencil, 2
parameters moment and angle depend on the temperature and the fluence.
C_PRAGER_MZ = cpr
Constant of Prager which makes it possible to define mixed work hardening.
Behavior
“DIS_CHOC”
:
COULOMB = driven
Value of the coefficient of friction
RIGI_NOR = kN
Value of the normal rigidity of shock. If RIGI_NOR is present it is this value which is taken in
count. If it is not present, the discrete elements to which one affects this material must have
their stiffness defined in addition (for example using control AFFE_CARA_ELEM with
key words DISCRETE or RIGI_PARASOL).
RIGI_TAN = Kt
Value of the tangential rigidity of shock
AMOR_NOR = Cn
Value of the normal damping of shock
AMOR_TAN = Ct
Value of the tangential damping of shock

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
137/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
DIST_1 = dist1
Outdistance characteristic of matter surrounding the first node of shock
DIST_2 = dist2
Outdistance characteristic of matter surrounding the second node of shock (shock between two structures
mobiles)
PLAY = d0
Outdistance between the node of shock and an obstacle not modelized (case of a shock between a structure
mobile and an indeformable and motionless obstacle).
Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
138/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
11.6 Key word factor
ASSE_CORN
: behavior of an assembly
bolted
11.6.1 Syntax
|
ASSE_CORN
=
_F
(
NU_1 = nu1
[R]
MU_1 = mu1
[R]
DXU_1
=
dxu1 [R]
DRYU_1
=
dryu1
[R]
C_1
=
c1
[R]
NU_2 = nu2
[R]
MU_2 = mu2
[R]
DXU_2
=
dxu2 [R]
DRYU_2
=
dryu2
[R]
C_2
=
c2
[R]
KY
=
ky
[R]
KZ
=
kz
[R]
KRX
=
krx
[R]
KRZ
=
krz
[R]
R_P0 =
/
rp0
[R]
/1.E-4
)
11.6.2 Operands
On the following figure, the plan
represent the plan of the assembly. The axis of the bolts is
perpendicular in this plan. The reader will refer to [U4.42.01]
AFFE_CARA_ELEM
for
orientation of the reference mark R
L
defining the plan of the assembly.
X
y
Z
R
L
Traces of the bolts
within assembly
The relation of behavior of the assembly is:
·
non-linear in translation according to X and rotation around Y.
·
linear according to the other degrees of freedom: DY, DZ, DRX, DRZ
Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
139/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
Behaviors in traction along axis X and rotation around axis Y.
NR
NU_1
NU_2
DXU_1
DX
C_1 * NU_1
C_2 * NU_2
DXU_2
My
MU_1
MU_2
DRYU_1
DRY
C_1 * MU_1
C_2 * MU_2
DRYU_2
The behavior of the connection is considered linear in the other directions:
KY
: stiffness in translation following Y
KZ
: stiffness in translation according to Z
KRX
: stiffness in rotation around X
KRZ
: stiffness in rotation around Z
R_P0: Slope in the beginning or of discharge
11.7 Key word factor
ARM
: behavior of a conductor arrangement
air
The arm of each armament of broken phase, represented by a discrete element, has one
non-linear behavior in force-displacement consisted the difference between displacement
maximum
dlp
end of the armament in the plastic phase and limiting elastic displacement
dle
.
11.7.1 Syntax
| ARM = _F
(
KYE
= kye
, [R]
DLE
= dle
, [R]
KYP
= kyp
, [R]
DLP
= dlp
, [R]
KYG
= kyg
, [R]
)
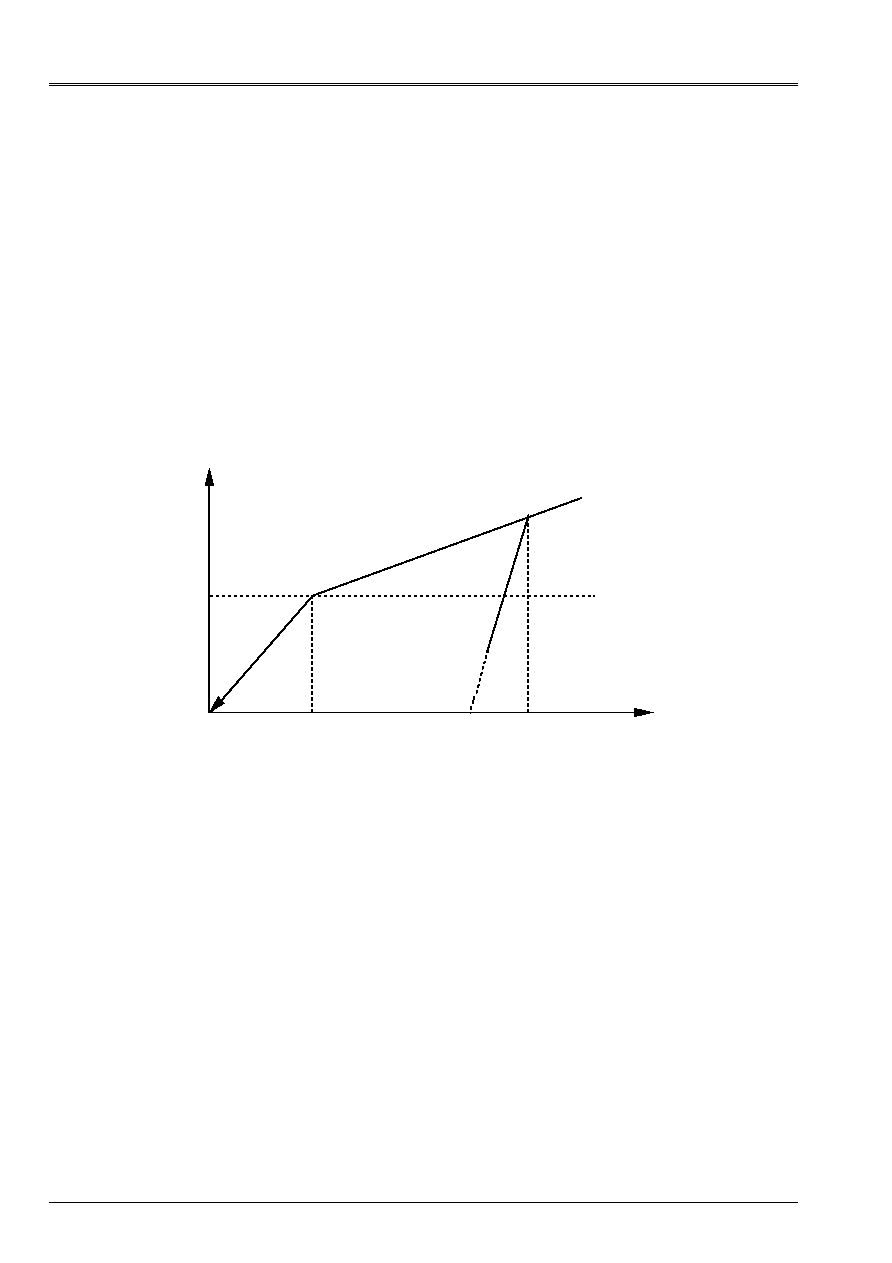
Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
140/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
11.7.2 Operand
KYE = kye
Elastic slope until a limiting effort.
DLE = dle
Displacement limits elastic strain.
KYP = kyp
Plastic slope until limiting displacement DLP.
DLP = dlp
Displacement limits plastic deformation 0.
KYG = kyg
Slope of discharge.
F
KYE
DLE
KYP
KYG
D

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
141/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
12 Behavior
fluid
12.1 Key word factor
FLUID
I
FLUID
Definitions of the constant characteristics of fluid.
12.1.1 Syntax
|
FLUID = _F
(
RHO
= rho
,
[R]
/
CELE_R
=
celr,
[R]
/
CELE_C
=
celc,
[C]
)
12.1.2 Operands
RHO
= rho
Density of the fluid. No the checking.
/CELE_R
= celr
Celerity of propagation acoustic waves in the fluid environment (standard reality).
No the checking of about size.
/
CELE_C
=
celc
Celerity of propagation acoustic waves in the fluid environment (standard complex
in particular for a porous environment). No the checking of about size.
For a modeling in
PHENOMENON: ACCOUSTICS
(control
AFFE_MODELE
[U4.41.01]) only
the definition of celerity using the key word
CELE_C
is valid.
The definition using the key word
CELE_R
conduit with a stop in error.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
142/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
13 Data Materials associated with postprocessings
13.1 Key word factor
TIRE
One will be able to refer to [R7.04.01].
13.1.1 Syntax
TIRE = _F (
/
WOHLER
=
f_wohl
,
[function]
/
A_BASQUIN
=
has
,
[R]
/
BETA_BASQUIN
=
,
[R]
/
A0
=
a0
,
[R]
/
A1
=
a1
,
[R]
/
A2
=
a2
,
[R]
/
A3
=
a3
,
[R]
/
SSL
=
SSL
,
[R]
MANSON_COFFIN
=
f_mans
,
[function]
E_REFE
=
EC.
,
[R]
D0
=
d0
,
[R]
TAU0 =
0
,
[R]
)
13.1.2 Operand
WOHLER
This operand makes it possible to introduce the curve of Wöhler of material in a form discretized not
by point. This function gives the number of cycles to the rupture NR
rupt
according to the half-amplitude
of stress
2
.
The curve of Wöhler is a function for which the user chooses the mode of interpolation:
·
LOG LOG
: interpolation logarithmic curve on the number of cycles to the rupture and on
half-amplitude of the stress (formula of Basquin per pieces),
·
FLAX FLAX
: linear interpolation on the number of cycles to the rupture and on the half amplitude
stress (this interpolation is disadvised because the curve of Wöhler is not absolutely
not linear in this reference mark),
·
FLAX LOG
: interpolation into linear on the half-amplitude of stress, and logarithmic curve on
the number of cycles to the rupture, which corresponds to the expression given by Wöhler.
The user must also choose the type of prolongation of the function on the right and on the left.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
143/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
13.1.3 Operands
A_BASQUIN
/
BETA_BASQUIN
A_BASQUIN
= has
BETA_BASQUIN =
These operands make it possible to introduce the curve of Wöhler of material in the analytical form of
BASQUIN [R7.04.01].
D = A Salt
where
With and
are two constants of material,
Salt = forced alternate of the cycle =
2
,
and D elementary damage.
Note:
Attention, in software POSTDAM, one gives constant A and
for D = A
it
who is not homogeneous with the 2 other mathematical expressions of the curve of
Wöhler.
13.1.4 Operands
A0
/
A1
/
A2
/
A3
/
SSL
A0
= a0
A1
= a1
A2
= a2
A3
= a3
SSL
= SSL
These operands make it possible to define in analytical form the curve of Wöhler in “current area”
[R7.04.01].
Salt
= alternate stress =
1
2
EC.
E
(
)
X
Salt
NR
D
NR
Salt
SSL
rupt
has
X has has X
X has
=
=
=
+
+
+
log
/
.
10
0
1
2
3
10
1
0
2
3
if
if not
This list of operands makes it possible to introduce the various parameters of this analytical form.
a0
,
a1
,
a2
and
a3
constants of material,
SSL
limit of endurance of material.
The Young modulus
E
is introduced into
DEFI_MATERIAU
(key word factor
ELAS
operand
E
).
The value of
EC.
, Young modulus associated with the curve with fatigue with material is also introduced
in
DEFI_MATERIAU
under the key word factor
TIRE
, operand
E_REFE
.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
144/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
13.1.5 Operand
MANSON_COFFIN
MANSON_COFFIN = f_mans
This operand makes it possible to introduce the curve of Manson-Whetstone sheath of material in a form
discretized point by point. This function gives the number of cycles to the rupture according to
half-amplitude of deformations
2
.
13.1.6 Operand
E_REFE
E_REFE = EC.
This operand makes it possible to specify the value of the Young modulus associated with the curve with fatigue with
material. This value allows amongst other things, to define the curve of Wöhler in “current area”
[R7.04.01].
13.1.7 Operand
D0
D0 = d0
Allows to specify the value of the limit of endurance in alternate pure traction and compression. This
value is used in the calculation of the criteria of Crossland and Dang Van Papadopoulos [R7.04.01]
by the control of
POST_FATIGUE
[U4.83.01].
13.1.8 Operand
TAU0
TAU0
=
0
Allows to specify the value of the limit of endurance in alternate pure shearing. This value is
used in the calculation of the criteria of Crossland and Dang Van Papadopoulos [R7.04.01] by
order
POST_FATIGUE
[U4.83.01].
13.2 Key word factor
DOMMA_LEMAITRE
DOMMA_LEMAITRE = _F (
S
=
S,
[function **]
EPSP_SEUIL = Pd, [function **]
EXP_S
=/
Pd, [R]
/
1.0, [DEFECT]
)
Under this key word factor are gathered all the characteristics material necessary to
calculation of the damage of Lemaitre and the law of Lemaitre-Sermage.
13.2.1 Operand
S
S = S
S
is a parameter material necessary to the calculation of the damage of Lemaitre.
S
must be one
function of the parameter
TEMP
.
13.2.2 Operand
EPSP_SEUIL
EPSP_SEUIL = Pd
Allows to specify the value of the threshold of damage
Pd
, necessary to the calculation of the damage
of Lemaitre.
13.2.3 Operand
EXP_S
XP_S = exp
Allows to define the law of Lemaitre-Sermage, the default value (1.0) corresponds to the calculation of
damage of Lemaitre

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
145/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
13.3 Key word factor CISA_PLAN_CRIT
CISA_PLAN_CRIT = _F (
MATAKE_A = has,
[R]
MATAKE_B = B,
[R]
ENDU_FT = endu_ft,
[R]
)
Under this key word factor are gathered all the characteristics material necessary to
implementation of the criteria with critical plans.
13.3.1 Operand MATAKE_A
MATAKE_A = has,
Allows to specify the value of the coefficient without dimension has, present in the criterion of MATAKE,
cf [R7.04.01] and [U4.83.02].
13.3.2 Operand MATAKE_B
MATAKE_B = B,
Allows to specify the value of the coefficient B, present in the criterion of MATAKE, cf [R7.04.01] and
[U4.83.02].
13.3.3 Operand ENDU_FT
ENDU_FT = endu_ft,
Allows to specify the value of the report/ratio of the limits of endurance in bending and alternating torsion,
cf [R7.04.01] and [U4.83.02]. This value must be higher or equal to one and lower or equal
with
3
.

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
146/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
13.4 Key word factor WEIBULL/WEIBULL_FO
Definition of the coefficients of the model of Weibull [R7.02.06].
Briefly, probability of cumulated rupture of rupture
P
R
of a structure is written, in the case of one
monotonous loading:
P
V
V
R
I
U
m
p
V
p
= -
-
1
0
exp
where the summation relates to the meshs
V
p
plasticized (i.e cumulated plastic deformation higher than
a value chosen arbitrarily
p
S
) and
m
V
U
,
,
0
are the parameters of the model of Weibull.
In the case of an unspecified way of loading:
()
P T
R
U
m
= -
-
1 exp
with:
()
{
}
()
{}
m
U T p U
I
V
m
U
V
V
=
<
>
max
~
, &
0
0
,
&p
indicating the rate of cumulated plastic deformation.
Lastly, if the stress of cleavage depends on temperature (WEIBULL_FO):
()
P T
R
U
m
= -
-
1
0
0
exp
,
0
indicating the stress of Weibull defined conventionally for
u0
data:
()
{
}
()
()
(
)
0
0
0
0
m
U T p U
V
U
I
U
m
U
U
V
V
=
<
>
max
.
, &
,
()
U
indicating the temperature in the element
V
.
13.4.1 Syntax
I
WEIBULL =
_F (
M
=
m
,
[R]
SIGM_REFE
=
U
,
[R]
VOLU_REFE
=
V0
,
[R]
SEUIL_EPSP_CUMU
=/PS
, [R]
/
10-6,
[DEFECT]
)
I
WEIBULL_FO = _F (
M
=
m
,
[R]
SIGM_REFE
=
U,
[function]
SIGM_CNV
=
0u
,
[R]
VOLU_REFE
=
V0
,
[R]
SEUIL_EPSP_CUMU
=/PS,
[R]
/
10-6,
[DEFECT]
)

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
147/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
13.4.2 Operands
M = m, SIGM_REFE:
U, SIGM_CNV:
0u, VOLU_REFE: V0
Parameters associated with the model with Weibull.
SEUIL_EPSP_CUMU = PS
Cumulated plastic deformation.
13.5 Key words factor RCCM/RCCM_FO
Definition of the sizes necessary to the use of the methods simplified defined in
payment RCC-M [R7.04.03]. These sizes are constant or function of the parameter “TEMP”.
13.5.1 Syntax
|
/
RCCM
= _F
(
SY_02 = sigm, [R]
SM
=
sigm,
[R]
KNOWN
=
sigm,
[R]
SC
=
sigm,
[R]
HS
=
sigm,
[R]
N_KE = H,
[R]
M_KE = m,
[R]
)
/
RCCM_FO
= _F (
SY_02 = sigm, [function]
SM
=
sigm,
[function]
KNOWN
=
sigm,
[function]
S = sigm, [function]
N_KE = H,
[function]
M_KE = m,
[function]
)

Code_Aster
®
Version
8.2
Titrate:
Operator
DEFI_MATERIAU
Date:
22/02/06
Author (S):
J.P. LEFEBVRE
Key
:
U4.43.01-I1
Page
:
148/148
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
13.5.2 Operand SY_02
Limit elastic with 0,2% of plastic deformation at the temperature of calculation. This operand can
to vary according to the temperature.
13.5.3 Operand SM
Acceptable stress equivalent of material to the temperature of calculation. This operand can vary in
function of the temperature.
13.5.4 Operand KNOWN
Tensile strength of material at the temperature of calculation. This operand can vary in function
temperature.
13.5.5 Operand SC
Working stress of material at the ambient temperature, cf RCCM.
13.5.6 Operand HS
Working stress of material at the maximum temperature, cf RCCM.
13.5.7 Operand S
Working stress of material. This operand varies according to the temperature, cf RCCM.
13.5.8 Operand N_KE_RCCM/M_KE_RCCM
N_KE_RCCM = N
M_KE_RCCM = m
These operands make it possible to define the values of N and m two constants of material.
These characteristics are necessary for the calculation of the elastoplastic coefficient of concentration
K
E
, which is defined by the RCC-M as being the relationship between the amplitude of real deformation and
the amplitude of deformation determined by the elastic analysis.
(
)
(
)
(
)
(
)
K
S
K
N
S
N m
S
ms
K
N
ms
E
m
E
m
m
m
E
m
=
= + -
-
-
<
<
=
1
3
1
1
3
1
1
3
3
1
3
if
if
if
/
/



















































































































































