
Code_Aster
®
Version
5.0
Titrate:
Elements of Fourier for the axisymmetric structures
Date:
21/12/00
Author (S):
X. DESROCHES
Key:
R3.06.04-A
Page:
1/12
Manual of Reference
R3.06 booklet: Machine elements and thermal for the continuous mediums
HI-75/00/006/A
Organization (S):
EDF/MTI/MN
Manual of Reference
R3.06 booklet: Machine elements and thermal for the continuous mediums
Document: R3.06.04
Elements of Fourier for the structures
axisymmetric
Summary
The elements of Fourier are intended to calculate the response of structure for axisymmetric geometry solicited
by nonaxisymmetric loadings broken up into Fourier series.
One exposes in this document a general theory of Analysis of Fourier with coupling of the symmetrical modes
and antisymmetric in the anisotropic case. The case of isotropic, or orthotropic materials of axis OZ, where
modes are uncoupled, is studied separately.
The elements of Fourier are usable in Code_Aster starting from modeling
AXIS_FOURIER
.
meshs supports of these elements are triangles and quadrangles of degree 1 and 2.
Code_Aster
®
Version
5.0
Titrate:
Elements of Fourier for the axisymmetric structures
Date:
21/12/00
Author (S):
X. DESROCHES
Key:
R3.06.04-A
Page:
2/12
Manual of Reference
R3.06 booklet: Machine elements and thermal for the continuous mediums
HI-75/00/006/A
1 Introduction
The analysis of Fourier is intended to calculate the response of structures for axisymmetric geometries
subjected to nonaxisymmetric loadings. In this case, it is necessary to develop them
loadings in Fourier series. Generally convergence is reached for 4 or 5 harmonics,
but the speed of this convergence depends on the nature of the loading: more the loading is
regular and more the corresponding series converges quickly. The most unfavourable case is that of one
force concentrated for which the practice shows that it is necessary to go to beyond (at least 7 harmonics).
In Code_Aster, the decomposition of the loading in Fourier series is supposed to be made
au préalable by the user. Code_Aster makes it possible to calculate the answers to this loading,
harmonic by harmonic (modeling
AXIS_FOURIER
), and overall after recombination of
harmonics between them (operators
COMB_CHAM_NO
and
COMB_CHAM_ELEM
).
One will expose in a first chapter the general framework of the anisotropy, while insisting on decoupling
modes in the orthotropic case. The second chapter clarifies the calculation of the matrix of rigidity
in the isotropic case.
For the use of the elements of Fourier in Code_Aster, one returns to the note of use of
modeling Fourier [U1.01.07].
2
Analyze of anisotropic Fourier
2.1 Theory
general
All the fields considered (forces, displacements, strains, stresses) are expressed in
cylindrical co-ordinates with following convention on the command of the components:
1 radial component according to R
2 axial component according to Z
3 tangential component according to
Example: (U
R
, U
Z
, U
), (F
R
, F
Z
, F
)
Z
R
U
Z
U
R
U
M
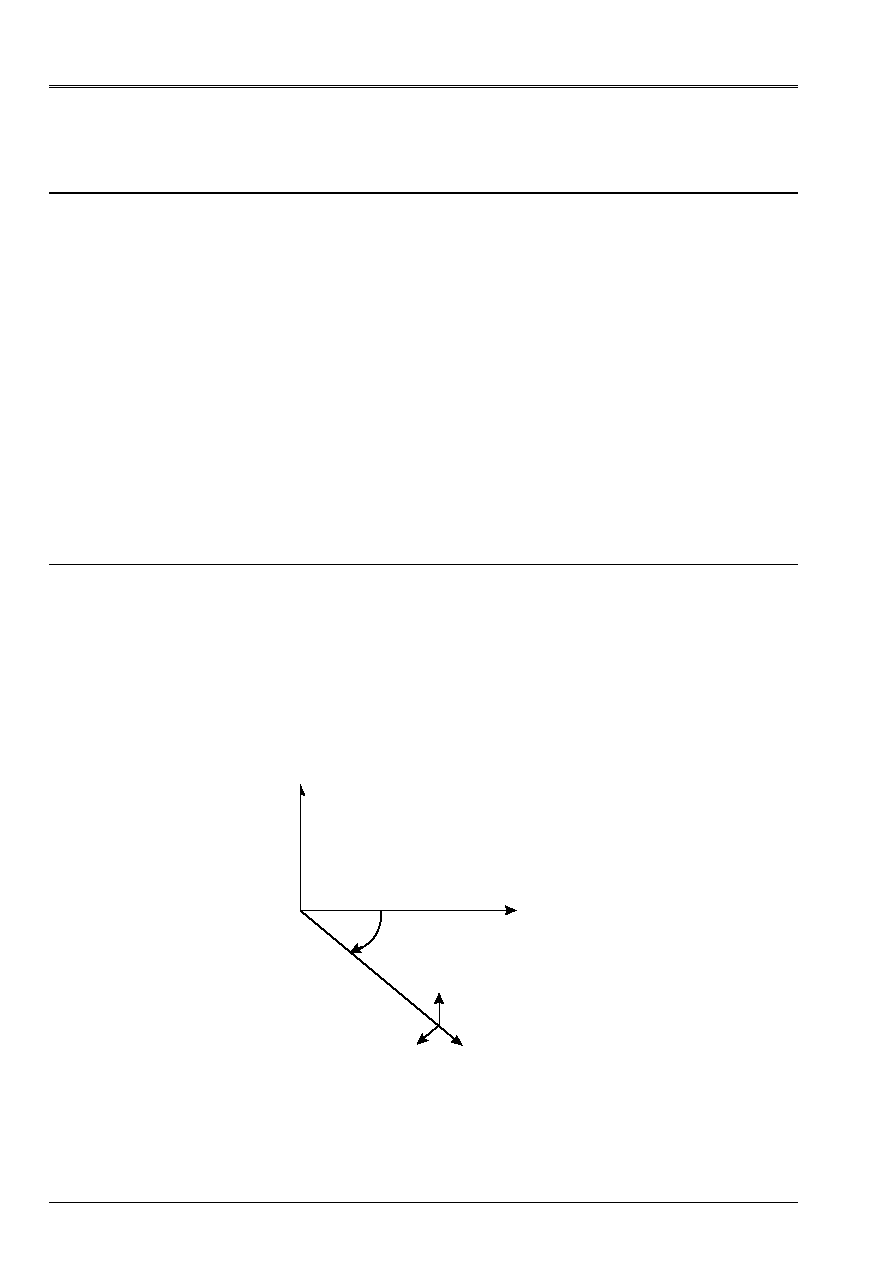
The mesh is localized in plan (R, Z), the symmetry of revolution being done around axis OZ.
trihedron (R, Z,
) is directed in the direct direction.
Code_Aster
®
Version
5.0
Titrate:
Elements of Fourier for the axisymmetric structures
Date:
21/12/00
Author (S):
X. DESROCHES
Key:
R3.06.04-A
Page:
3/12
Manual of Reference
R3.06 booklet: Machine elements and thermal for the continuous mediums
HI-75/00/006/A
Z
R
R
ez
C
E
R
Displacement is broken up
U
(or the loading
F
) according to
U U
U
U
=
+
S
has
S
where
(resp.
U
has
)
indicate the symmetrical part (resp. antisymmetric) of the development in Fourier series of
U
by
report/ratio with the variable
.
One obtains:
()
()
()
(
)
()
()
()
U
U R Z
L
U
v R Z
L
U
W R Z
L
U
U
U R Z
L
U
v R Z
L
U
W R Z
L
U
rs
ls
L
zs
ls
L
S
ls
L
S
ruffle
L
za
L
has
L
has
=
=
=
-
=
=
=
=
=
=
=
=
=
0
0
0
0
0
0
, cos
, cos
,
sin
, sin
, sin
, cos
symmetrical part
antisymmetric part
To note the choice of the sign for
U
S
, which makes it possible to simplify later calculations. If one notes
(
) (
)
U
U
ls
ls
ls
ls
L
has
U v W
=
,
resp.
L
-
ième symmetrical component (resp. antisymmetric) of
development in Fourier series of
U
, one obtains:
U
U
U
=
-
+
=
cos
cos
sin
sin
sin
cos
L
L
L
L
L
L
ls
L
has
L
0
0
0
0
0
éq 2.1-1
Code_Aster
®
Version
5.0
Titrate:
Elements of Fourier for the axisymmetric structures
Date:
21/12/00
Author (S):
X. DESROCHES
Key:
R3.06.04-A
Page:
4/12
Manual of Reference
R3.06 booklet: Machine elements and thermal for the continuous mediums
HI-75/00/006/A
If one indicates by
the vector deformation linearized, one realizes that
can be broken up into
following Fourier series:
====
=
=
=
=
cos
sin
sin
cos
,
,
,
,
L I
L I
L I
L I
ls
L
L
has
4
4 2
2 4
2
4
4 2
2 4
2
0
0
0
0
0
-
+
éq 2.1-2
with
{
}
=
R
Z
rz
R
Z
,
,
,
ls
ls ls
L
has
L
has
B
B
=
=
U
U
with (see [bib1]):
B
R
Z
R
L
R
Z
R
L
R
R
R
L
R
Z
ls
=
-
-
0
0
0
0
1
0
0
0
1
0
One has
B
B
L
ls
=
(this is due to the choice of the symmetrical development of
U
in (cos, cos, sin) with the place
of (cos, cos, sin)). One will omit starting from now the indices
has
S
and and one will note
B
L
the operator
allowing to calculate the deformations corresponding to the harmonic
L
.
2.2
Coupling and decoupling of the symmetrical and antisymmetric modes
By taking again the preceding notations, one a:
U
U
U
=
=
=
=
cos
sin
sin
cos
,
,
,
,
L I
L
L I
L
ls
L
L
L
has
2
2 1
1 2
2
2 1
1 2
0
0
0
0
-
+

Code_Aster
®
Version
5.0
Titrate:
Elements of Fourier for the axisymmetric structures
Date:
21/12/00
Author (S):
X. DESROCHES
Key:
R3.06.04-A
Page:
5/12
Manual of Reference
R3.06 booklet: Machine elements and thermal for the continuous mediums
HI-75/00/006/A
what is written, by introducing matrices
M
M
ls
and
:
(
)
U
U
U
U
U
U
=
+
=
+
M
M
M
M
ls
L
S
L
has
L
L
ls
ls
L
has
One deduces from it that:
L
L
S ls
L
with
M
M
=
+
'
'
with
M
L I
L I
M
L I
L I
ls
L
has
'
cos
sin
'
sin
cos
,
,
,
,
=
-
=
4
4 2
2 4
2
4
4 2
2 4
2
0
0
0
0
Calculation of the deformation energy
W
D dsd
ds rdrdz
D
MR. DM
ds
D
MR. DM
ds
D
MR. DM
ds
D
MR. DM
ds
MR. DM
L I
L I
L
H T L
S
T ls T ls
L
S ls
T T
L
with
S
S
T T
L
S ls
T ls T ls
L
with
S
S
L
has
L
S
=
=
=
+
+
+
=
with
Since
0
2
0
2
0
2
0
2
0
2
4
2
0
0
'
'
'
'
'
'
'
'
'
'
sin
cos
(
)
(
)
-
=
-
-
D
D
D
D
L I
L I
MR. DM
D
L
L
D
L
D
L
D
L
L
T
L
has
L
S
T
1
3
3
2
4
2
1
3
2
3
2
2
0
0
cos
sin
'
'
sin
cos
sin
cos
sin
cos
and that
sin
cos
,
L
L D
D
=
=
0
0
3
0
2
if
there is thus no term
(
) (
)
T the ls
T ls
,
,
or
in
W
.
There is then no coupling
(
) (
)
U U
U U
has
S
S
has
,
,
or
.

Code_Aster
®
Version
5.0
Titrate:
Elements of Fourier for the axisymmetric structures
Date:
21/12/00
Author (S):
X. DESROCHES
Key:
R3.06.04-A
Page:
6/12
Manual of Reference
R3.06 booklet: Machine elements and thermal for the continuous mediums
HI-75/00/006/A
2.3
Calculation of the stresses
Just as
,
can be broken up into following Fourier series:
(
)
=
+
M
M
ls
L
S
L
has
L
has
L
'
'
Law of Hooke
=
D
, one deduces:
=
-
-
+
cos
sin
cos
sin
sin
cos
sin
cos
L D
L D
L D
L D
L D
L D
L D
L D
T
L
L
S
T
L
has
1
3
3
2
1
3
3
2
Maybe, while revealing the matrices
M
M
L
S
L
has
'
'
and
:
=
+
-
+
-
+
M
D
D
D
D
M
D
D
D
D
ls
L
S
T
L
has
L
L
has
T
ls
L
has
'
'
,
,
,
,
,
,
,
,
1
4 2
2 4
2
4 4
3
3
2 2
4 4
3
3
2 2
1
4 2
2 4
2
0
0
0
0
0
0
0
0
While posing
D D
D
D
D
D
S
has
T
1
4 2
2 4
2
4 4
3
3
2 2
0
0
0
0
,
,
,
,
= -
and
, one deduces the parts from them symmetrical and
antisymmetric of the stress relating to the harmonic
L
:
L
S
S ls
with
S L ls
L has
L
has
ls has
S
L ls has
S L
D
D
D B
D B
D
D
D B
D B
=
+
=
+
= -
+
= -
+
U
U
U
U
éq 2.3-1
Note:
In the case of the orthotropism compared to OZ, one has
D
has
=
0
and [éq 2.1-1] is reduced to:
L
S
S L ls
L
has
S L
D B
D B
=
=
U
U
I.e. if displacements are symmetrical (or antisymmetric), the stresses are it
too.

Code_Aster
®
Version
5.0
Titrate:
Elements of Fourier for the axisymmetric structures
Date:
21/12/00
Author (S):
X. DESROCHES
Key:
R3.06.04-A
Page:
7/12
Manual of Reference
R3.06 booklet: Machine elements and thermal for the continuous mediums
HI-75/00/006/A
3
Calculation of the matrix of rigidity
3.1 Case
General
Are
U
and
two unspecified fields kinematically acceptable. By applying the principle of
virtual work with the element of volume
v
, one can write:
()
()
T
T
v
v
FD
U F FD
.
.
=
After decomposition in Fourier series and integration compared to
, one obtains, for fields
ls
ls
U U
,
,
A.C. unspecified and for any harmonic
L
:
(
)
(
)
T
ls
ls T
S
L
T
ls
ls T
S
L
L
L
ds
U F
U F
ds
.
.
.
.
+
=
+
Maybe, while using [éq 2.3-1] and while posing:
K
B D B ds
K
B D B ds
K
K
K
B D B ds
ls
H T S L L
S
H T S L L
S
ls
L
mow
H T has L L
S
L
L
L
=
=
=
=
=
One obtains the system of equations according to:
K U
K U
F
K U
K U
F
L ls
mow
ls
T tired ls
L
+
=
+
=
éq 3-1
where
T
mow
mow
K
K
= -
it is seen that if
D
has
0
, the decoupling of the modes in symmetrical harmonics and
antisymmetric is not possible any more. On the other hand, if
D
has
=
0
(orthotropism compared to OZ) then
K
mow
=
0
and [éq 3-1] is reduced to:
K U
F
K U
F
L
ls
ls
L
=
=
While taking for vectors displacement (resp. force) corresponding to the harmonic
L
vectors:
{
}
{
}
U
F
L
rs
zs
S
ruffle
za
has
L
L
rs
zs
S
ruffle
za
has
L
U U U U U U
F
F
F
F
F
F
=
=
,
,
,
,
,
,
,
,
Code_Aster
®
Version
5.0
Titrate:
Elements of Fourier for the axisymmetric structures
Date:
21/12/00
Author (S):
X. DESROCHES
Key:
R3.06.04-A
Page:
8/12
Manual of Reference
R3.06 booklet: Machine elements and thermal for the continuous mediums
HI-75/00/006/A
One has then:
K
K
K
K
K
K
lg
L
L
lg
L
mow
T tired
L
U
F
=
=
with
3.2 Calculation
of
K
lg
in the isotropic case
In this case one thus has
K
mow
=
0
. One details in the continuation the calculation of
K
B D B ds
L S H T S L L
L
=
In the isotropic case, one a:
D D
D
D
D
D
D
D
D
D
D
D
D
D
S
=
=
1
2
2
0
2
1
2
0
2
2
1
0
0
0
0
3
0
0
3
0
0
3
(
)
(
) (
)
(
) (
)
(
)
with
D
E
D
E
D
E
1
1
1
1 2
2
1
1 2
3 2 1
=
-
+
-
= +
-
=
+
One can write:
R
Z
rz
R
Z
L
rs
zs
S
L
T
R
Z
R
Z
R
Z
B
U
U
U
B
U
R
U
R
U
R
U
R
U
R
U
R
U
Z
U
Z
U
Z
=
=
'
,
,
,
,
,
,
,
,
0
0
0
1 0
0
0 0
0
0
0
0
0 0
0
0 1
0
1
0
0 0
0
0 0
0
0
0
0
0 1
0
1 0
0
0
1 0 0
1
0 0
0
0
0
0 0
0
0 0
1
-
-
L
L
L
fcts of form
derived from the fcts of form
with
B L
'
=

Code_Aster
®
Version
5.0
Titrate:
Elements of Fourier for the axisymmetric structures
Date:
21/12/00
Author (S):
X. DESROCHES
Key:
R3.06.04-A
Page:
9/12
Manual of Reference
R3.06 booklet: Machine elements and thermal for the continuous mediums
HI-75/00/006/A
While indicating by
{}
W
J J
N
=
1
with the functions of form of the element considered, one a:
U
U
R
U
R
U
R
U
R
U
R
U
R
U
Z
U
Z
U
Z
W
R
W
R
W
R
W
R
W
R
W
R
W
Z
R
Z
R
Z
R
Z
J
J
J
J
J
J
J
J
=
=
!
“# $
!
!
!
!
!
!
!
!
!
!
!
!
0
0
0
0
0
0
0
0
0
0
0
0
0
0
node
()
()
()
!
!
!
!
% & '
!
0
0
0
0
W
Z
W
Z
U J
U J
U J
J
P
J
R
Z
J
block
One notes
()
(
)
P
P
P
NR
=
1
,
,
!
where
NR
is the number of nodes of the element.
Then
K
P B D B P ds
L
T
T
L
L
L
S
L
=
'
'
K
L
symmetrical and is made of blocks
()
K
L
I J
,
3 3
×
:
()
K
P B D B P ds
L
I J
T I H T
L
J
L
S
L
,
'
'
=

Code_Aster
®
Version
5.0
Titrate:
Elements of Fourier for the axisymmetric structures
Date:
21/12/00
Author (S):
X. DESROCHES
Key:
R3.06.04-A
Page:
10/12
Manual of Reference
R3.06 booklet: Machine elements and thermal for the continuous mediums
HI-75/00/006/A
The calculation of the blocks
()
K
L
I J
,
is clarified below:
(
)
(
)
Tb D B
D
D
L D
D
D
lD
D
L D
lD
L D
D
L D
D
lD
D
lD
D
lD
D
D
D
D
lD
D
D
D
D
D
lD
D
D
lD
D
L
L
'
'
=
+
-
+
-
+
+
-
-
-
-
-
-
1 1
3
0
1
3
2
0
3
0
2
0
0
3
0
0
0
0
0
0
3
1
3
0
1
3
2
0
3
0
2
0
2
0
2
1
0
0
0
2
0
0
0
0
0
3
0
3
0
0
3
0
3
0
0
3
0
0
0
0
0
0
0
3
0
3
0
0
2
0
2
2
0
0
0
1
0
0
3
0
0
0
0
0
0
3
2
2
2
()
=
× =
=
+
+
+
T I H T
L
J
ijl
I J
I J
I J
I J
I J
I J
I J
I J
I J
I J
I
J
I
J
I
J
P B D B P
K
I J
K
K
K
K
K
K
K
K
K
K
D
L D
R
W W
D Wr Wr D Wz Wz
'
'
,
,
,
,
,
,
,
,
,
,
,
3 3
1
3
1
3
11
12
13
21
22
23
31
32
33
11
2
2
with
+
+
=
+
+
=
+
+
+
-
+
D
R W
W
R
W
W
R
K
L D
R
W W
D
W
R
W
R
D Wz Wz
K
L D
D
R
W W
D
W
R
W
R
W
Z
W
Z
D
R W
W
R
W
R W
I
J
J
I
I J
I
J
I
J
I
J
I J
I
J
I
J
I
J
I
J
I
J
2
3
3
1
1
3
3
3
22
2
2
33
2
2
,
,
(
)
(
)
K
D
W
R
W
Z
D
W
Z
W
R
D
R W
W
Z
K
D
W
R
W
Z
D
W
Z
W
R
D
R W
W
Z
K
L
R
D
D W W
L
R D W
W
R
L
R D W
W
R
K
L
R
D
D W W
L
R D W
I J
I
J
I
J
I
J
I J
I
J
I
J
J
I
I J
I
J
J
I
I
J
I J
I
J
I
12
21
13
2
31
2
2
3
2
3
2
2
1
3
2
3
1
3
2
,
,
,
,
=
+
+
=
+
+
= -
+
-
+
= -
+
-
W
R
L
R D W
W
R
K
L
R D
W
Z W
L
R D W
W
Z
K
L
R D W
W
Z
L
R D
W
Z W
J
J
I
I J
I
J
I
J
I J
I
J
I
J
+
= -
+
= -
+
3
2
3
2
3
23
32
,
,
Blocks
K
I J
,
are not symmetrical except for
I
J
=
(on the diagonal of
K
). One notices in
fact that blocks
K
I J
,
can be written for any harmonic (
L
=
0
included/understood).

Code_Aster
®
Version
5.0
Titrate:
Elements of Fourier for the axisymmetric structures
Date:
21/12/00
Author (S):
X. DESROCHES
Key:
R3.06.04-A
Page:
11/12
Manual of Reference
R3.06 booklet: Machine elements and thermal for the continuous mediums
HI-75/00/006/A
K
K
L D
R W W
K
K
L D
R W W
K
K
L D
R W W
K
K
K
K
K
L K
K
L K
K
L K
K
L K
I J
I J
I
J
I J
I J
I
J
I J
I J
I
J
I J
I J
I J
I J
I J
I J
I J
I J
I J
I J
I J
I J
11
11
2
2
22
22
2
2
33
33
2
2
12
12
21
21
13
13
31
31
23
23
32
32
0
3
0
3
0
1
0
0
0
0
0
0
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
=
+
=
+
=
+
=
=
= -
= -
= -
= -
where blocks
K
I J
0
,
are independent of the harmonic
L
.
4 Loadings
It is supposed that the loading was broken up according to the same base which displacements, that is to say:
F
F
F
=
-
+
=
cos
cos
sin
sin
sin
cos
L
L
L
L
L
L
ls
L
0
0
0
0
0
There is not coupling for the same harmonic between the parts symmetrical and antisymmetric of
loading because of orthogonality of the goniometrical functions
sin
cos
L
L
and
, this for all
types of loading. This wants to say in particular that the equivalent nodal forces are them
same for the harmonics symmetrical and antisymmetric if amplitudes
F
F
ls
and
are them
same.
For the nature of the acceptable loadings with Fourier modeling, one returns to the note
of use [U1.01.07].

Code_Aster
®
Version
5.0
Titrate:
Elements of Fourier for the axisymmetric structures
Date:
21/12/00
Author (S):
X. DESROCHES
Key:
R3.06.04-A
Page:
12/12
Manual of Reference
R3.06 booklet: Machine elements and thermal for the continuous mediums
HI-75/00/006/A
5
Conclusion and Outlines
Currently, it is supposed that the decomposition of the loading was made as a preliminary by the user,
i.e.
{
}
F F
ls
the L
,
0
is known. This decomposition could be carried out by an operator
of Code_Aster which would project the loading on the modes of Fourier.
For the moment, only the nonanisotropic case is established, i.e. it y forever coupling of
modes. The extension to the anisotropy can constitute a later development.
6 Bibliography
[1]
DUVAUT G.: “Mechanical of the continuous mediums” p282
[2]
ASKA HS. : “Axisymmetric Structures in Fourier series”, May 1982, ISD











