
Code_Aster
®
Version
6.2
Titrate:
Note of use of the model of thin hull thermal
Date:
22/01/02
Author (S):
A. Mr. DONORE, F. VOLDOIRE
Key
:
U2.03.03-A
Page
:
1/6
Instruction manual
U2.03 booklet: Thermomechanical
HT-66/02/003/A
Organization (S):
EDF/AMA
Instruction manual
U2.03 booklet: Thermomechanical
Document: U2.03.03
Note of use of the mean model of hull
thermics
Summary
Determination of the field of temperature in a mean structure subjected to various conditions
thermics can be done advantageously using the model of thin hull thermal describes in [R3.11.01].
The temperature is described by three scalar fields, noted
TEMP, TEMP_INF
,
TEMP_SUP
defined on
surface average (X
) of the hull, which will have to be with a grid, and by a distribution in thickness X
3
data by
:
T (X
, X
3
) =
TEMP
(X
)
P
1
(X
3
) +
TEMP_INF
(X
)
P
2
(X
3
) +
TEMP_SUP
(X
)
P
3
(X
3
)
functions
P
1,
P
2
and
P
3
being given. In this model, the curvature of the hull does not intervene.
One can treat the stationary situations, as well as the problems of evolution. The latter must however
to respect a limitation: it is necessary that the moments T
C
characteristics of the evolution of the loadings
are such as:
T
C
> C
33
H
2
with:
·
C: voluminal heat of material constitutive of the hull,
·
H: half thickness of the hull,
·
33
: coefficient of transverse conductivity.
One gives here the description of the Aster controls useful for calculation, classified by chronological functionalities.
Code_Aster
®
Version
6.2
Titrate:
Note of use of the model of thin hull thermal
Date:
22/01/02
Author (S):
A. Mr. DONORE, F. VOLDOIRE
Key
:
U2.03.03-A
Page
:
2/6
Instruction manual
U2.03 booklet: Thermomechanical
HT-66/02/003/A
1
Management of work: mesh
The process of the most general mesh of an unspecified surface in
IR
3
being the triangularisation,
one must thus constitute a mesh by triangles of the average surface of the hull, plunged in
IR
3
. That can be done with
IDEAS
and procedure
PRE_IDEAS
for the conversion of the universal file
IDEAS
[U4.13.01].
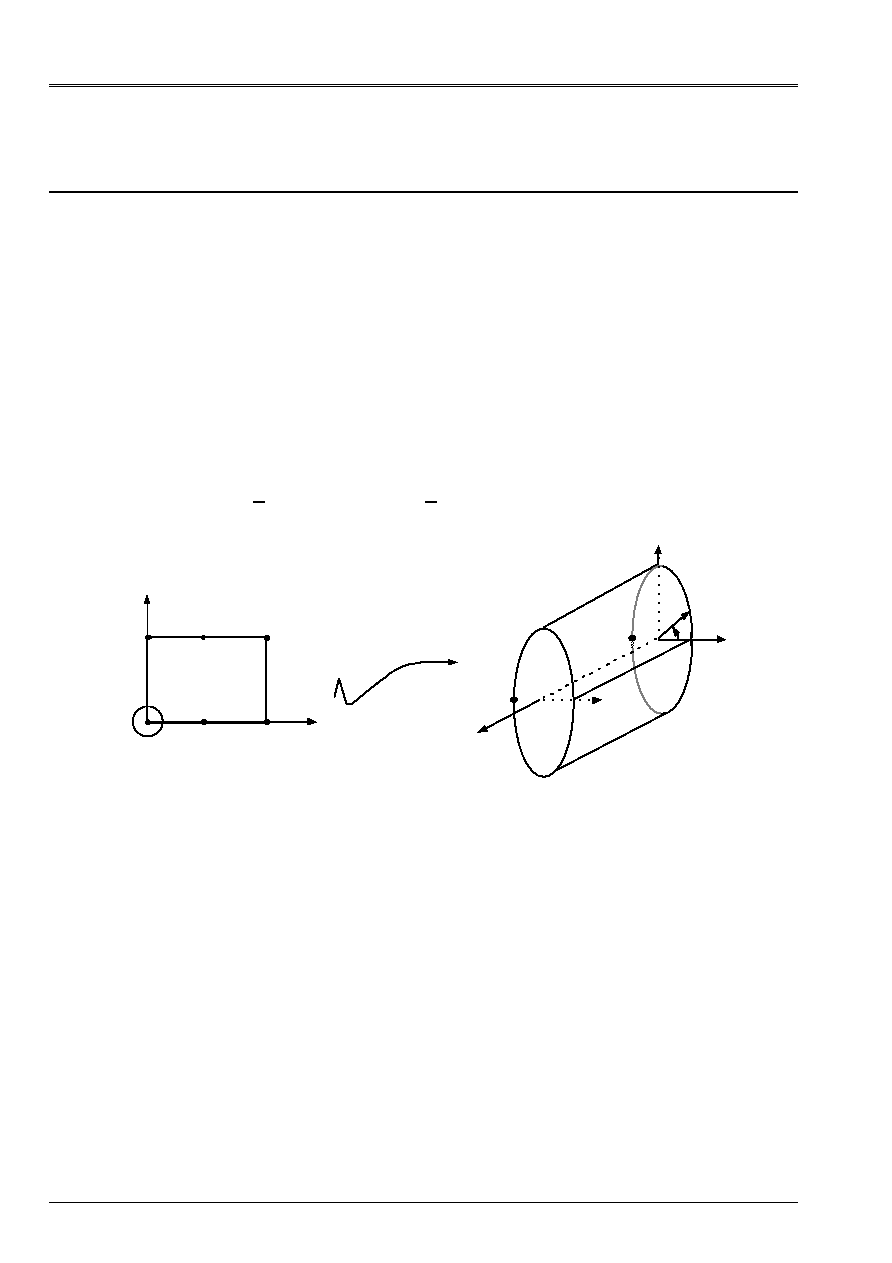
In the case of a plate or of a cylinder, one can use
Ali-baba
and procedure
PRE_ALIBABA
for the conversion [U4.13.02], which generates a mesh plunged in IR
3
.
Example:
PRE_ALIBABA
(
PLATE
: /“YES”
/
“NOT”
[DEFECT]
ROLL:
(R: radius)
);
In the case of the cylinder plane mesh
(X, Y)
of
Ali-baba
is transformed into a mesh:
(X = R cos X
R
, y = R sin X
R
, Z = Y)
in
IR
3
, where
R
is the radius.
X
y
Y
0
X
2
R
Z
D
B
F
With
C
E
X/R
F
D
C
B
With
E
Z
The cylinder created by rolling up of the plate 2D is of axis
Z
>
0
; the wall external with the cylinder
corresponds to the face higher 2D
Z
>
0
.
The equations of the thermics of hull being of command 2, one will be able to use to net:
·
triangles with 3 nodes (which will give P1 elements),
·
triangles with 6 nodes (for of P2).

Code_Aster
®
Version
6.2
Titrate:
Note of use of the model of thin hull thermal
Date:
22/01/02
Author (S):
A. Mr. DONORE, F. VOLDOIRE
Key
:
U2.03.03-A
Page
:
3/6
Instruction manual
U2.03 booklet: Thermomechanical
HT-66/02/003/A
2
Modeling, characteristics, material, loadings
·
To describe for example the materials, the loadings…, one can use constants,
functions or of the tablecloths with the operators
DEFI_CONSTANTE
,
DEFI_FONCTION
or
DEFI_NAPPE
[U4.21.01, - .02, - .03].
·
To affect the finite elements on the mesh, the operator is used
AFFE_MODELE
way
following:
MOD = AFFE_MODELE
(
MESH:
my
[mesh]
AFFE:
(
ALL
:
“YES”
PHENOMENON: “THERMAL”
MODELING:
“HULL”)
);
·
To assign the geometrical characteristics to the elements, in fact the thickness, one must
to use the operator
AFFE_CARA_ELEM
[U4.24.01]:
= AFFE_CARA_ELEM will cara
(
MODEL: MOD
[model]
HULL:
(
ALL
:
“YES”
THICK: thick
);
·
The definition of materials and their assignment with the mesh are made in a usual way [U4.23.01 and
- .02].
·
The assignment of the thermal loadings is done using the operators
AFFE_CHAR_THER
or
AFFE_CHAR_THER_F
[U4.25.02]. The various key words usable are:
I
TEMP_IMPO
:
(
/NODE
: lno
/
GROUP_NO
: lgno
I
TEMP
:
T
1
[R]
or
[function]
I
TEMP_INF
: T
2
[R]
or
[function]
I
TEMP_SUP
: T
3
[R]
or
[function]
);
One can thus choose
ddl
who will have specified values.
I
EXCHANGE
:
(
/
ALL
:
“YES”
/
NET
:
lma
/
GROUP_MA
:
lgma
I
COEF_H_INF
:
hinf [R]
or
[function]
TEMP_EXT_INF
:
tinf [R]
or
[function]
I
COEF_H_SUP
:
hsup [R]
or
[function]
TEMP_EXT_SUP
:
tsup [R]
or
[function]
);
One thus gives the coefficients of exchange and the outside air temperatures on the walls
higher and lower. It should be noted that the coefficients of exchange also intervene in
the expression of “rigidity” in the equations, and not only (as for the temperatures
external) in the second members.

Code_Aster
®
Version
6.2
Titrate:
Note of use of the model of thin hull thermal
Date:
22/01/02
Author (S):
A. Mr. DONORE, F. VOLDOIRE
Key
:
U2.03.03-A
Page
:
4/6
Instruction manual
U2.03 booklet: Thermomechanical
HT-66/02/003/A
Note:
The model considered here neglects the curvature of the hull. However [R1.03.01.] if the thickness
hull is not weak enough compared to the average radius of curvature, it is preferable
to correct the values of the coefficients of exchange, or else one makes an error on
temperature about:
hinf - hsup
hinf + hsup
* thick
radius
The correction is as follows:
COEF_H_INF
: the value
hinf
multiplied by (
1 - thick X courbure_moyenne
).
COEF_H_SUP
: the value
hsup
multiplied by (
1 + thick X courbure_moyenne
),
·
For the plates, that does not take place to be.
·
For the cylinders, the correction will be respectively:
(1 + thick/radius)
,
(1 - thick/radius)
.
I
FLUX_REP
:
(
/
ALL
:
“YES”
/
NET
:
lma
/
GROUP_MA
: lgma
I
FLUX_INF
: finf [R]
or
[function]
I
FLUX_SUP
: fsup [R]
or
[function]
)
One thus provides the values of the flows imposed on the 2 faces of the hull.
Note:
As for the coefficients of exchange (see above), one can be brought to correct them
flow in higher or lower wall by:
(
thick 1±. courbure_moyenne
).

Code_Aster
®
Version
6.2
Titrate:
Note of use of the model of thin hull thermal
Date:
22/01/02
Author (S):
A. Mr. DONORE, F. VOLDOIRE
Key
:
U2.03.03-A
Page
:
5/6
Instruction manual
U2.03 booklet: Thermomechanical
HT-66/02/003/A
3
TOTAL control: elementary calculation, assembly,
resolution
One can be useful oneself of the total control
THER_LINEAIRE
for a stationary calculation [U4.33.02].
temp =
THER_LINEAIRE
(
MODEL: MOD
CHAM_MATER
:
chechmate
TEMP_INIT
:
(
STATIONARY: “yes”)
EXCIT:
(
CHARGE: cht
FONC_MULT: coeff
[function]
)
CARA_ELEM: will cara
);
Or one can use the core operators:
mel =
CALC_MATR_ELEM
(
OPTION
:
“RIGI_THER”
[U4.41.01]
MODEL
: MOD
,
CHAM_MATER
:
chechmate
,
CARA_ELEM
: will cara,
CHARGE
: cht
);
vel =
CALC_VECT_ELEM
(
OPTION
:
“CHAR_THER”
[U4.41.02]
MODEL
: MOD
,
CHAM_MATER
:
chechmate
,
CARA_ELEM
: will cara,
CHARGE
: cht
);
naked
= NUME_DDL
(
MATR_RIGI
: mel
);
[U4.42.01]
my =
ASSE_MATRICE
(
MATR_ELEM
: mel
[U4.42.02]
NUME_DDL
: naked
);
vecas =
ASSE_VECTEUR
(
VECT_ELEM
: vel
[U4.42.03]
NUME_DDL
: naked
);
&ma
=
FACT_LDLT
(
MATR_ASSE
: my
);
[U4.51.01]
temper = RESO_LDLT
(
MATR_FACT
: my,
[U4.51.02
]
CHAM_NO
:
vecas
);
If one wishes to solve a problem of evolution, one will be able to use a decomposition on
space clean modes [R1.03.01].
One must initially build the matrix of “mass”, then to solve the problem with the eigenvalues
associated. For that one uses the succession of the operators (with the concepts created previously
described:
mel
,
naked
,
my
).

Code_Aster
®
Version
6.2
Titrate:
Note of use of the model of thin hull thermal
Date:
22/01/02
Author (S):
A. Mr. DONORE, F. VOLDOIRE
Key
:
U2.03.03-A
Page
:
6/6
Instruction manual
U2.03 booklet: Thermomechanical
HT-66/02/003/A
melma =
CALC_MATR_ELEM
(
OPTION
:
“MASS_THER”
[U4.41.01]
MODEL
: MOD
,
CHAM_MATER
:
chechmate
,
CARA_ELEM
: will cara,
CHARGE
: cht
);
mama =
ASSE_MATRICE
(
MATR_ELEM
:
melma
[U4.42.02]
NUME_DDL
: naked
,
);
modeth = MODE_ITER_INV
(
MATR_A
:
my
,
[U4.52.01]
MATR_B
: mama,
CALC_FREQ: (LIST_FREQ: l_f)
);
4
Post processing of calculation
The calculation of the heat transfer rates in the structure can be done using the following operator:
flu = CALC_CHAM_ELEM
(
MODEL
:
MOD
CHARGE
:
cht
TEMPLE
: temper
CARA_ELEM
: will cara
CHAM_MATER
:
chechmate
OPTION
:
/
“FLUX_ELNO_TEMP”
/
“FLUX_ELGA_TEMP”
);
The option
“FLUX_ELNO_TEMP”
allows to calculate flows with the nodes of each element by
interpolation (the concept result is well a field with the elements).
The option
“FLUX_ELGA_TEMP”
allows to calculate flows at the points of GAUSS of each element.
5
Impressions of results
The procedure will be used
IMPR_RESU
:
IMPR_RESU
(
MODEL
: MOD
RESU
:
(
CHAM_GD: nom_cham)
);
nom_cham
, indicating a concept of the type:
temperature
,
flow
… (field with the nodes or field with
elements).
Example:
IMPR_RESU
(MODEL
: MOD
RESU:
(CHAM_GD: temper),
RESU
:
(CHAM_GD
:
flu)
);





