
Code_Aster
®
Version
8.2
Titrate:
Operators
AFFE_CHAR_THER
and
THER_F
Date:
22/02/06
Author (S):
X. DESROCHES
Key
:
U4.44.02-I1
Page
:
1/28
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
Organization (S):
EDF-R & D/AMA
Instruction manual
U4.4- booklet: Modeling
Document: U4.44.02
Operators
AFFE_CHAR_THER
and
AFFE_CHAR_THER_F
1 Goal
To affect loadings and boundary conditions thermal on a model.
For the operator
AFFE_CHAR_THER,
the affected values do not depend on any parameter and are
defined by actual values.
For the operator
AFFE_CHAR_THER_F
, the values are related to one or two parameters to be chosen
as a whole (
INST, X, Y, Z
) or of the temperature
TEMP
in nonlinear thermics.
These functions must be defined beforehand by the call to one of the operators:
·
DEFI_CONSTANTE
[U4.31.01]
·
DEFI_FONCTION
[U4.31.02]
·
DEFI_NAPPE
[U4.31.03]
·
CALC_FONC_INTERP
[U4.32.01]
The produced concept is of char_ther type.

Code_Aster
®
Version
8.2
Titrate:
Operators
AFFE_CHAR_THER
and
THER_F
Date:
22/02/06
Author (S):
X. DESROCHES
Key
:
U4.44.02-I1
Page
:
2/28
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
2 Syntax
general
CH [char_ther] = AFFE_CHAR_THER
(
MODEL
= Mo,
[model]
|
TEMP_IMPO =
(see key word TEMP_IMPO
[§
4.4]
)
|
FLUX_REP =
(see key word FLUX_REP
[§ 4.5])
|
RADIATION
=
(see key word RADIATION
[§ 4.7])
|
EXCHANGE =
(see key word EXCHANGE
[§ 4.8])
|
SOURCE =
(see key word SOURCE
[§ 4.9])
|
GRAD_TEMP_INIT
=
(see key word GRAD_TEMP_INIT [§ 4.10])
|
LIAISON_DDL
=
(see key word LIAISON_DDL
[§ 4.11])
|
LIAISON_GROUP = (see key word LIAISON_GROUP
[§ 4.12])
|
LIAISON_MAIL =
(see key word LIAISON_MAIL [§
4.13])
|
ECHANGE_PAROI = (see key word ECHANGE_PAROI
[§ 4.14])
|
LIAISON_UNIF =
(see key word LIAISON_UNIF [§
4.15])
|
LIAISON_CHAMNO= (see key word LIAISON_CHAMNO [§ 4.16])
|
CONVECTION=
(see key word CONVECTION
[§ 4.17])
)
CH [char_ther] = AFFE_CHAR_THER_F
(
MODEL
= Mo,
[model]
|
TEMP_IMPO =
(see key word TEMP_IMPO
[§
4.4]
)
|
FLUX_REP =
(see key word FLUX_REP
[§ 4.5])
|
FLUX_NL =
(see key word FLUX_NL
[§ 4.6])
|
RADIATION
=
(see key word RADIATION
[§ 4.7])
|
EXCHANGE =
(see key word EXCHANGE
[§ 4.8])
|
SOURCE =
(see key word SOURCE
[§ 4.9])
|
GRAD_TEMP_INIT= (see key word GRAD_TEMP_INIT [§ 4.10])
|
LIAISON_DDL
=
(see key word LIAISON_DDL
[§ 4.11])
|
LIAISON_GROUP = (see key word LIAISON_GROUP
[§ 4.12])
|
ECHANGE_PAROI = (see key word ECHANGE_PAROI
[§ 4.14])
|
LIAISON_UNIF =
(see key word LIAISON_UNIF [§
4.15])
|
CONVECTION =
(see key word CONVECTION
[§ 4.17])
)

Code_Aster
®
Version
8.2
Titrate:
Operators
AFFE_CHAR_THER
and
THER_F
Date:
22/02/06
Author (S):
X. DESROCHES
Key
:
U4.44.02-I1
Page
:
3/28
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
3 General information
Possible error messages related to the control
AFFE_CHAR_THER
It happens sometimes that a thermal ordering of calculation (
THER_LINEAIRE
,
THER_NON_LINE
,…)
stop in fatal error during the calculation of the second elementary members due to the loadings
defined in the controls
AFFE_CHAR_THER_xx
.
When the code stops during these elementary calculations, important information of the message
of error is the name of the option of calculation requested by the code.
The name of this option is in general unknown to the user and it is thus difficult for him to include/understand
the message.
In the table below, one gives in with respect to the names of the options of calculation, the name of
order and key word factor which make it possible to activate this option.
Elementary option of calculation
Order
Key word factor
CHAR_THER_FLUNL AFFE_CHAR_THER_F
FLUX_NL
CHAR_THER_FLUN_F AFFE_CHAR_THER_F
FLUX_REP
CHAR_THER_FLUN_R AFFE_CHAR_THER
FLUX_REP
CHAR_THER_FLUTNL AFFE_CHAR_THER
CONVECTION
CHAR_THER_FLUTNL AFFE_CHAR_THER_F
CONVECTION
CHAR_THER_FLUX_F AFFE_CHAR_THER_F
FLUX_REP
CHAR_THER_FLUX_R AFFE_CHAR_THER
FLUX_REP
CHAR_THER_GRAI_F AFFE_CHAR_THER_F
GRAD_TEMP_INIT
CHAR_THER_GRAI_R AFFE_CHAR_THER
GRAD_TEMP_INIT
CHAR_THER_PARO_F AFFE_CHAR_THER_F
ECHANGE_PAROI
CHAR_THER_PARO_R AFFE_CHAR_THER
ECHANGE_PAROI
CHAR_THER_SOUR_F AFFE_CHAR_THER_F
SOURCE
CHAR_THER_SOUR_R AFFE_CHAR_THER
SOURCE
CHAR_THER_TEXT_F AFFE_CHAR_THER_F
EXCHANGE
CHAR_THER_TEXT_R AFFE_CHAR_THER
EXCHANGE

Code_Aster
®
Version
8.2
Titrate:
Operators
AFFE_CHAR_THER
and
THER_F
Date:
22/02/06
Author (S):
X. DESROCHES
Key
:
U4.44.02-I1
Page
:
4/28
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
4 Operands
4.1
General information on the operands
4.1.1 Two forms of operands under a key word factor
The operands under a key word factor are of two forms:
·
operands specifying the topological entities where the loadings (key words are affected
GROUP_NO
and
GROUP_MA
, etc…). The arguments of these operands are identical for both
operators.
·
operands specifying the affected values (
TEMP
,
COEF_H
, etc…). Significance of
these operands is the same one for the two operators but the arguments of these operands are
all the real type for the operator
AFFE_CHAR_THER
and of the type
function
(created by one of
operators
DEFI_FONCTION
,
DEFI_NAPPE
,
DEFI_CONSTANTE
or
CALC_FONC_INTERP
) for
the operator
AFFE_CHAR_THER
_F
.
We will thus not distinguish in this document, except mention express of the opposite, both
operators
AFFE_CHAR_THER
and
AFFE_CHAR_THER_F
.
4.1.2 Topological entities of assignment of the loadings
In a general way, the topological entities on which values must be affected are
defined:
·
by nodes and in this case:
-
maybe by the operand
GROUP_NO
allowing to introduce a list of group of nodes,
-
maybe by the operand
NODE
allowing to introduce a list of nodes.
·
by mesh and in this case:
- is
by
GROUP_MA
allowing to introduce a list of groups of meshs,
- is
by
NET
allowing to introduce a list of meshs.
Regulate:
To define the field of assignment most simply possible, one uses the rule of
overload it is the last assignment which precedes.
4.2 Operand
MODEL
MODEL
= Mo,
Concept produced by the operator
AFFE_MODELE
[U4.41.01] where the types of elements are defined
stop affected on the mesh.

Code_Aster
®
Version
8.2
Titrate:
Operators
AFFE_CHAR_THER
and
THER_F
Date:
22/02/06
Author (S):
X. DESROCHES
Key
:
U4.44.02-I1
Page
:
5/28
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
4.3 Key word
TEMP_IMPO
4.3.1 Drank
Key word factor usable to impose, on nodes or groups of nodes, a temperature.
According to the name of the operator called, the values are provided directly (
AFFE_CHAR_THER
) or
via a concept of the type
function
(
AFFE_CHAR_THER_F)
.
4.3.2 Syntax
·
for
AFFE_CHAR_THER
TEMP_IMPO = _F (
|
ALL =
“YES”,
|
NODE =
lno,
[l_noeud]
|
GROUP_NO
=
lgno,
[l_gr_noeud]
|
NET
= lma, [l_maille]
|
GROUP_MA
= lgma,
[l_gr_maille]
/TEMP =
T,
[R]
/
|
TEMP = T,
[R]
|
TEMP_INF
= tinf,
[R]
|
TEMP_SUP
= tsup,
[R]
)
·
for
AFFE_CHAR_THER_F
TEMP_IMPO = _F (
|
ALL =
“YES”,
|
NODE =
lno,
[l_noeud]
|
GROUP_NO
=
lgno,
[l_gr_noeud]
|
NET
= lma, [l_maille]
|
GROUP_MA
= lgma,
[l_gr_maille]
/
TEMP =
tf,
[function]
/
|
TEMP = tf,
[function]
|
TEMP_INF
=
tinf,
[function]
|
TEMP_SUP
=
tsupf,
[function]
/
EVOL_THER
=
evth,
[evol_ther]
DDL
=
“TEMP”,
)
4.3.3 Operands
/TEMP
=
Value of the temperature imposed on (S) the node (S) specified (S).
/
For the elements of thermal hull only
(
Modeling:
“HULL”):
|
TEMP
Temperature on the average layer imposed on (S) the node (S) specified (S).
|
TEMP_INF
Temperature imposed on the lower wall of the hull.

Code_Aster
®
Version
8.2
Titrate:
Operators
AFFE_CHAR_THER
and
THER_F
Date:
22/02/06
Author (S):
X. DESROCHES
Key
:
U4.44.02-I1
Page
:
6/28
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
|
TEMP_SUP
Temperature imposed on the higher wall of the hull: cf “Note of use of the model
of thermal thin hull " in booklet [U2].
These options make it possible to represent a parabolic variation of the temperature in
the thickness.
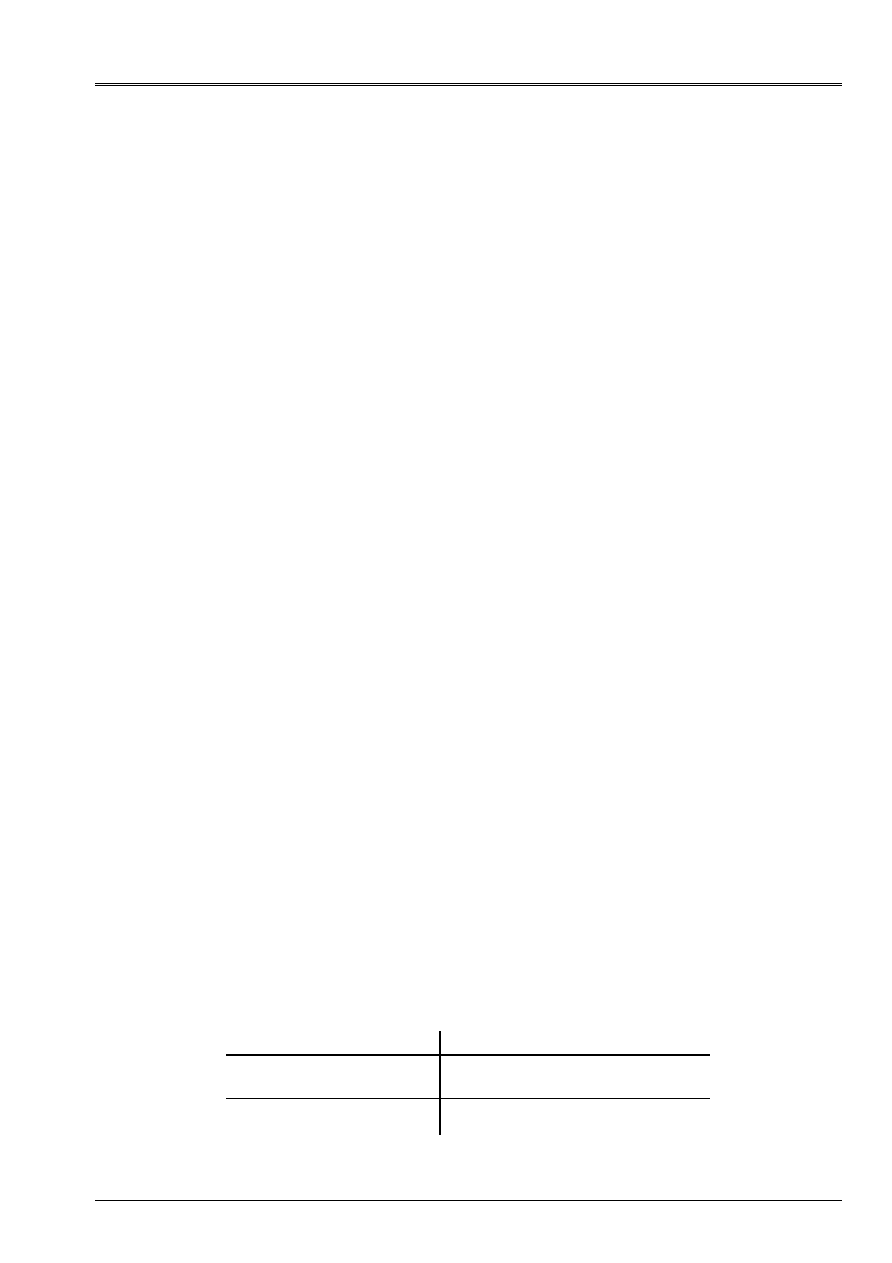
Note:
The hull is directed by the connectivity of the nodes of the associated mesh (cf [U3.01.00]).
That is to say
N
the normal vector directing the hull:
Lower wall
N
Higher wall
/EVOL_THER
=
(for
AFFE_CHAR_THER_F
only)
Allows to affect on nodes an imposed temperature given via a structure of data
evol_ther calculated beforehand. In each node, one extracts from the evol_ther a function
TEMP = F (INST) and one affects this function like imposed temperature.
This possibility exists currently only for the degree of freedom “TEMP”.
Code_Aster
®
Version
8.2
Titrate:
Operators
AFFE_CHAR_THER
and
THER_F
Date:
22/02/06
Author (S):
X. DESROCHES
Key
:
U4.44.02-I1
Page
:
7/28
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
4.4 Word
key
FLUX_REP
4.4.1 Drank
Key word factor usable to apply normal flows, with a face of voluminal element or of
thermal hull defined by one or more meshs or of the groups of meshs of the triangle type or
quadrangle. This key word also makes it possible to apply a normal flow to an edge (in
2D
PLAN
or
AXIS
or
AXIS_FOURIER
) on meshs of the segment type.
According to the name of the operator called, the values are provided directly (
AFFE_CHAR_THER
) or
via a concept of the type
function
(
AFFE_CHAR_THER_F)
.
4.4.2 Syntax
·
for
AFFE_CHAR_THER
FLUX_REP = _F
(
/
ALL =
“YES”,
/
|
NET
= lma, [l_maille]
|
GROUP_MA
= lgma,
[l_gr_maille]
/
FLUN =
fl,
[R]
/
|
FLUN_INF
= flin,
[R]
|
FLUN_SUP
= flsup,
[R]
)
·
for
AFFE_CHAR_THER_F
FLUX_REP = _F
(
/
ALL =
“YES”,
/
|
NET
= lma, [l_maille]
|
GROUP_MA
= lgma,
[l_gr_maille]
/
FLUN
=
flf, [function]
/
|
FLUN_INF
= flinf,
[function]
|
FLUN_SUP
= flsupf, [function]
/
|
FLUX_X
= flx, [function]
|
FLUX_Y
= fly, [function]
|
FLUX_Z
= flz, [function]
)
4.4.3 Operands
/
FLUN: fl
normal flow imposed on the mesh.
This loading applies to the types of meshs and following modelings:
Net Modélisation
TRIA3, TRIA6,
QUAD4, QUAD8, QUAD9
3D, 3d_DIAG
SEG2, SEG3
PLAN, AXIS, AXIS_FOURIER,
PLAN_DIAG, AXIS_DIAG
Code_Aster
®
Version
8.2
Titrate:
Operators
AFFE_CHAR_THER
and
THER_F
Date:
22/02/06
Author (S):
X. DESROCHES
Key
:
U4.44.02-I1
Page
:
8/28
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
More precisely the boundary condition applied is:
(
)
grad.
T N
=
fl
where is thermal conductivity and
N
is the normal directed in the direction of the classification of
nodes of the mesh. The convention of orientation is that used in
AFFE_CHAR_MECA
[U4.44.01].
/
|
FLUN_INF = flin
|
FLUN_SUP = flsup
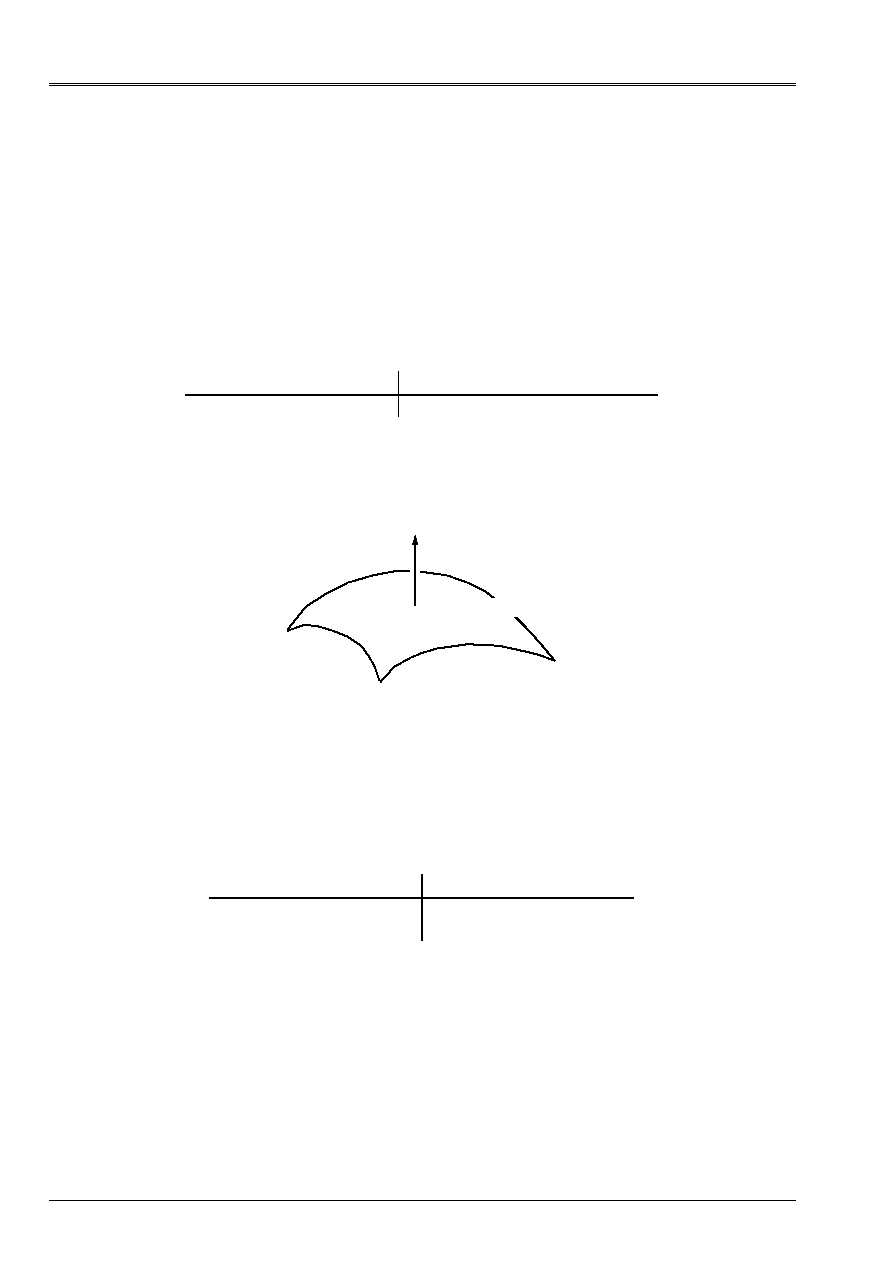
Normal flow imposed on the walls lower and higher of a thermal hull.
These loadings apply to the types of meshs and following modelings:
Net Modélisation
TRIA3, TRIA6
HULL
N
being the normal directing surface [U4.44.01], the boundary condition applied is:
(
)
grad.
T
N
=
flin
where
flin
is the normal flow imposed on the lower wall of the hull,
(
)
grad.
T
N
=
flsup
where
flsup
is the normal flow imposed on the higher wall of the hull.
Lower wall
N
Higher wall
/
|
FLUX_X = flx
|
FLUX_Y = fly
|
FLUX_Z = flz
Vectorial flow in the total reference mark (only for
AFFE_CHAR_THER_F)
that one projects on
the normal with the element (for the definition of the normal [U4.44.01]).
This loading applies to the types of meshs and modelings:
Net Modélisation
SEG2, SEG3
PLAN
PLAN_DIAG

Code_Aster
®
Version
8.2
Titrate:
Operators
AFFE_CHAR_THER
and
THER_F
Date:
22/02/06
Author (S):
X. DESROCHES
Key
:
U4.44.02-I1
Page
:
9/28
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
4.5 Key word
FLUX_NL
4.5.1 Drank
Key word factor usable to apply normal flows functions of the temperature, with a face
of voluminal element defined by one or more meshs or of the groups of meshs of the triangle type
or quadrangle. This key word also makes it possible to apply a normal flow to an edge (in
2D
PLAN
or
AXIS
) on meshs of the segment type. One can thus modelize a condition of radiation of
law type of STEPHAN. This type of flow is used only by the controls
THER_NON_LINE
[U4.54.02] and THER_NON_LINE_MO [U4.54.03].
The values are provided by a concept of the type
function
.
4.5.2 Syntax
·
For
AFFE_CHAR_THER_F
FLUX_NL = _F (
/
ALL =
“YES”,
/
|
NET
= lma, [l_maille]
|
GROUP_MA
= lgma,
[l_gr_maille]
FLUN =
fl, [function]
)
4.5.3 Operands
FLUN:
normal flow imposed on the mesh.
This loading applies to the types of meshs and following modelings:
Net Modélisation
TRIA3, TRIA6,
QUAD4, QUAD8, QUAD9
3D, 3d_DIAG
SEG2, SEG3
PLAN, AXIS
PLAN_DIAG, AXIS_DIAG
More precisely the boundary condition applied is:
(
)
grad.
T
N
=
fl
where is the normal directed in the direction of the classification of the nodes of the mesh. Orientation
used in
AFFE_CHAR_MECA
document [U4.44.01].

Code_Aster
®
Version
8.2
Titrate:
Operators
AFFE_CHAR_THER
and
THER_F
Date:
22/02/06
Author (S):
X. DESROCHES
Key
:
U4.44.02-I1
Page
:
10/28
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
4.6 Key word
RADIATION
4.6.1 Drank
Key word allowing to define the flow radiated ad infinitum according to the formula:
by the data of emissivity, the Boltzmann constant
and the temperature ad infinitum
expressed
into Centigrade. The temperature T will be it also expressed into Centigrade, it is thus necessary to take care, by coherence, with
to use only degrees Celsius for all the study.
4.6.2 Syntax
·
for
AFFE_CHAR_THER
RADIATION = _F (
/
ALL =
“YES”,
/
|
NET =
lma,
[l_maille]
|
GROUP_MA =
lgma,
[l_gr_maille]
SIGMA
=
sigma,
[R8]
EPSILON
=
epsilon,
[R8]
TEMP_EXT=
tex, [R8]
)
·
for
AFFE_CHAR_THER_F
RADIATION = _F (
/
ALL =
“YES”,
/
|
NET =
lma,
[l_maille]
|
GROUP_MA =
lgma,
[l_gr_maille]
SIGMA
=
sigma,
[function]
EPSILON
=
epsilon,
[function]
TEMP_EXT=
tex, [function]
)
4.6.3 Operands
SIGMA =
sigma
EPSILON =
epsilon
TEMP_EXT
= tex
This loading applies to following modelings:
Net Modélisation
TRIA3, TRIA6,
QUAD4, QUAD8, QUAD9
3D, 3d_DIAG
SEG2, SEG3
PLAN,
AXIS
PLAN_DIAG, AXIS_DIAG
sigma:
Boltzmann constant,
= 5.67 10
8
in units IF (W/m
2
.K
4
) (attention with this
value if the units of mesh change),
epsilon: emissivity,
tex:
temperature ad infinitum in degrees Celsius.

Code_Aster
®
Version
8.2
Titrate:
Operators
AFFE_CHAR_THER
and
THER_F
Date:
22/02/06
Author (S):
X. DESROCHES
Key
:
U4.44.02-I1
Page
:
11/28
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
4.7 Key word
EXCHANGE
4.7.1 Drank
Key word factor usable to apply conditions of exchange with an outside air temperature
with a face of voluminal elements or hulls, defined by one or more meshs or of the groups
meshs of the triangle type or quadrangle. This key word also makes it possible to apply conditions
of exchange to an edge (in 2D
PLAN
or
AXIS
or
AXIS_FOURIER
) on meshs of the segment type.
According to the name of the operator called, the values are provided directly (
AFFE_CHAR_THER
) or
via a concept of the type
function
(
AFFE_CHAR_THER_F)
.
4.7.2 Syntax
·
for
AFFE_CHAR_THER
EXCHANGE = _F (
/
ALL =
“YES”,
/
|
NET
= lma, [l_maille]
|
GROUP_MA
= lgma,
[l_gr_maille]
/
COEF_H
= H,
[R]
TEMP_EXT
= tex, [R]
/
|
COEF_H_INF =
hin, [R]
TEMP_EXT_INF
=
texin,
[R]
|
COEF_H_SUP =
hsup,
[R]
TEMP_EXT_SUP = texsup,
[R]
)
·
for
AFFE_CHAR_THER_F
EXCHANGE = _F (
/
ALL =
“YES”,
/
|
NET
= lma, [l_maille]
|
GROUP_MA
= lgma,
[l_gr_maille]
/
COEF_H =
HF, [function]
TEMP_EXT
= texf,
[function]
/
|
COEF_H_INF =
hinf,
[function]
TEMP_EXT_INF =
texinf,
[function]
|
COEF_H_SUP =
hsupf,
[function]
TEMP_EXT_SUP =
texsupf,
[function]
)
Code_Aster
®
Version
8.2
Titrate:
Operators
AFFE_CHAR_THER
and
THER_F
Date:
22/02/06
Author (S):
X. DESROCHES
Key
:
U4.44.02-I1
Page
:
12/28
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
4.7.3 Operands
/
COEF_H = H,
TEMP_EXT = tex,
This loading applies to the types of meshs and following modelings:
Net Modélisation
TRIA3, TRIA6,
QUAD4, QUAD8, QUAD9
3D, 3d_DIAG
SEG2, SEG3
PLAN, PLAN_DIAG
AXIS, AXIS_FOURIER,
AXIS_DIAG
More precisely the boundary condition applied is:
where
N
is the normal directed in the direction of the classification of the nodes nodes (orientation
used in
AFFE_CHAR_MECA
[U4.44.01]).
/
|
COEF_H_INF =
hin,
TEMP_EXT_INF
= texin,
|
COEF_H_SUP =
hsup,
TEMP_EXT_SUP
= texsup,
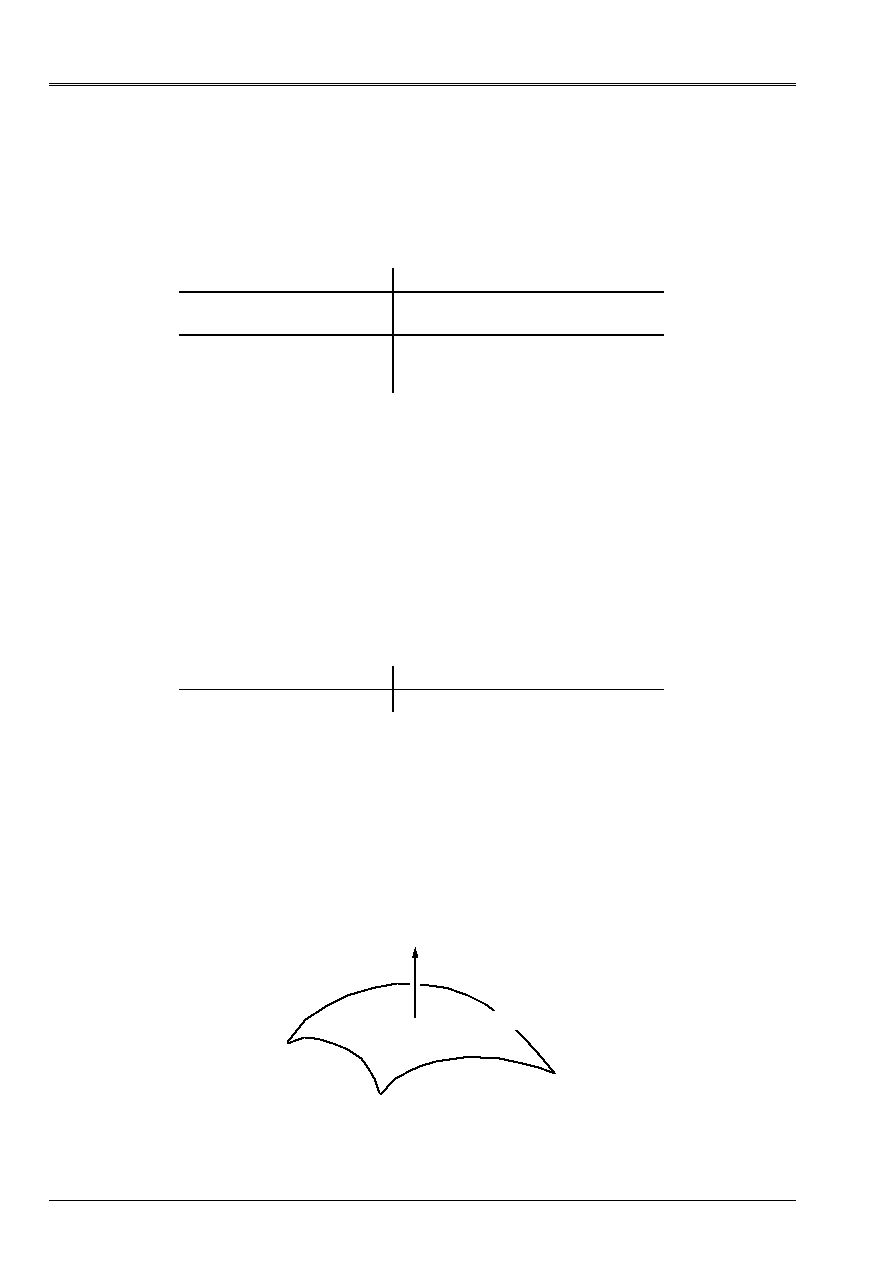
This loading applies to the types of meshs and following modelings:
Net Modélisation
TRIA3, TRIA6
HULL
N
being the normal directing surface [U3.01.00], the boundary condition applied is:
where
hin
coefficient of exchange on the lower wall of the hull,
and
texin
outside air temperature, with dimensions lower wall.
where
hsup
coefficient of exchange on the higher wall of the hull,
and
texsup
outside air temperature, with dimensions external wall.
Lower wall
N
Higher wall

Code_Aster
®
Version
8.2
Titrate:
Operators
AFFE_CHAR_THER
and
THER_F
Date:
22/02/06
Author (S):
X. DESROCHES
Key
:
U4.44.02-I1
Page
:
13/28
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
4.8 Key word
SOURCE
4.8.1 Drank
Key word factor usable to apply voluminal sources (2D or 3D) to a definite field
by one or more meshs or groups of meshs of the voluminal type.
According to the name of the operator called, the values are provided directly (
AFFE_CHAR_THER
) or
via a concept of the type
function
(
AFFE_CHAR_THER_F)
.
4.8.2 Syntax
·
for
AFFE_CHAR_THER
SOURCE=_F
(
/
ALL =
“YES”,
/
|
NET =
lma,
[l_maille]
|
GROUP_MA
= lgma,
[l_gr_maille]
SOUR =
S,
[R]
/
SOUR_CALCULEE
=
chs, [cham_elem_sour_R]
)
·
for
AFFE_CHAR_THER_F
SOURCE=_F
(
/
ALL =
“YES”,
/
|
NET =
lma,
[l_maille]
|
GROUP_MA
= lgma,
[l_gr_maille]
SOUR =
sf,
[function]
)
4.8.3 Operands
This loading applies to the types of meshs and following modelings:
Net Modélisation
HEXA8, HEXA20, HEXA27
PYRA5, PYRA13,
PENTA6, PENTA15
TETRA4, TETRA10
3D, 3d_DIAG
TRIA3, TRIA6,
QUAD4, QUAD8, QUAD9
PLAN, PLAN_DIAG,
AXIS, AXIS_FOURIER
AXIS_DIAG
/
SOUR = S,
Value of the presumedly constant source on the element.
/
SOUR_CALCULEE = chs,
Name of
cham_elem_sour_R
containing on each element the values of the source
discretized at the points of Gauss (1
era
family).

Code_Aster
®
Version
8.2
Titrate:
Operators
AFFE_CHAR_THER
and
THER_F
Date:
22/02/06
Author (S):
X. DESROCHES
Key
:
U4.44.02-I1
Page
:
14/28
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
4.9 Key word
GRAD_TEMP_INIT
4.9.1 Drank
Key word factor usable to apply to an element 3D or 2D (
PLAN
,
AXIS
) a gradient of
presumedly uniform temperature in the element. This “initial” variation in temperature is usable by
example to solve the elementary problems determining the correctors of linear thermics
stationary in the basic airframe (2D, 3D), in periodic homogenization.
The coefficients of homogenized conductivity are obtained while calculating by operator POST_ELEM
[U4.81.22] key word ENER_POT the energy dissipated thermically with balance in linear thermics with
to leave the correctors.
Because of the thermal analogy, this step can be exploited to obtain the correctors in
elasticity antiplane in the basic 2D cell, as well as in electric conduction.
The assignment can be done on one or more meshs, one or more groups of meshs or on all
elements of the model.
4.9.2 Syntax
·
for
AFFE_CHAR_THER
GRAD_TEMP_INIT = _F (
/
ALL =
“YES”,
/
|
NET
= lma, [l_maille]
|
GROUP_MA
= lgma,
[l_gr_maille]
|
FLUX_X
=
flx, [R]
|
FLUX_Y
=
fly, [R]
|
FLUX_Z
=
flz, [R]
)
4.9.3 Operands
This loading applies to the types of meshs and following modelings:
Net Modélisation
TRIA3, TRIA6,
QUAD4, QUAD8, QUAD9
PLAN, AXIS,
PLAN_DIAG, AXIS_DIAG
HEXA8, HEXA20,
HEXA27
PENTA6, PENTA15,
TETRA4, TETRA10
PYRA5, PYRA13
3D, 3d_DIAG
|
FLUX_X = flx (flxf)
|
FLUX_Y = fly (flyf)
|
FLUX_Z = flz (flzf) (in 3D only)
Components of the variation in temperature
in the total reference mark.
The second calculated elementary member is:
where
is the tensor of
thermal conductivities.

Code_Aster
®
Version
8.2
Titrate:
Operators
AFFE_CHAR_THER
and
THER_F
Date:
22/02/06
Author (S):
X. DESROCHES
Key
:
U4.44.02-I1
Page
:
15/28
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
The gradients can be a function of the geometry and/or time.
·
for
AFFE_CHAR_THER_F
GRAD_TEMP_INIT = _F (
/ALL =
“YES”,
/MESH =
lma,
[l_maille]
/
GROUP_MA
= lgma,
[l_gr_maille]
|
FLUX_X
=
flxf,
[function]
|
FLUX_Y
=
flyf,
[function]
|
FLUX_Z
=
flzf,
[function]
)

Code_Aster
®
Version
8.2
Titrate:
Operators
AFFE_CHAR_THER
and
THER_F
Date:
22/02/06
Author (S):
X. DESROCHES
Key
:
U4.44.02-I1
Page
:
16/28
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
4.10 Key word
LIAISON_DDL
4.10.1 Drank
Key word factor usable to define a linear relation between degrees of freedom of two or
several nodes.
According to the name of the operator called, the values are provided directly (
AFFE_CHAR_THER
) or
via a concept
function
(
AFFE_CHAR_THER_F
).
4.10.2 Syntax
·
for
AFFE_CHAR_THER
LIAISON_DDL = _F (
/NODE =
lno,
[l_noeud]
/
GROUP_NO
= lgno,
[l_gr_noeud]
DDL
=
|
“TEMP”, [DEFECT]
|
“TEMP_INF”,
|
“TEMP_SUP”,
COEF_MULT
=
I
,
[l_R]
COEF_IMPO
=
,
[R]
)
·
for
AFFE_CHAR_THER_F
LIAISON_DDL = _F (
/NODE =
lno,
[l_noeud]
/
GROUP_NO
= lgno,
[l_gr_noeud]
DDL
=
|
“TEMP”, [DEFECT]
|
“TEMP_INF”,
|
“TEMP_SUP”,
COEF_MULT
=
I
,
[l_R]
COEF_IMPO
=
F
,
[function]
)
4.10.3 Operands
The list of the nodes NR
I
(I = 1, R) defined by
GROUP_NO
or
NODE
is ordered in a natural way:
·
in the order of the list of group of nodes, and for each group of nodes, in the order
of definition of the group by
GROUP_NO
.
·
in the order of the list of nodes for
NODE
.
The argument of
DDL
must be a list of degrees of freedom T
I
(I = 1, R) of R texts taken among:
“TEMP”
“TEMP_SUP”
“TEMP_INF”
If the key word
DDL
is omitted, by defect the linear relation will relate to the degrees of freedom
“TEMP”
.
The argument of
COEF_MULT
must be a list
I
(I = 1, R) of coefficients (of real type for
AFFE_CHAR_THER
and
AFFE_CHAR_THER_F
).

Code_Aster
®
Version
8.2
Titrate:
Operators
AFFE_CHAR_THER
and
THER_F
Date:
22/02/06
Author (S):
X. DESROCHES
Key
:
U4.44.02-I1
Page
:
17/28
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
The argument of
COEF_IMPO
is a coefficient for
AFFE_CHAR_THER
, a function of space
for
AFFE_CHAR_THER_F
.
The following kinematic condition is applied:
Note:
Components
“TEMP_SUP”
and
“TEMP_INF”
can intervene only in
combinations only assigned to nodes which belong to elements of hull
(modeling
“HULL”
).
In the case of a linear relation between the degrees of freedom of the same node, one will repeat
behind the key word
NODE
the name of the node as many time as there are degrees of freedom in
relation. Example: to impose T
sup
= T
inf
on the N1 node, one will write:
LIAISON_DDL = _F (NODE = (N1, N1),
DDL
=
(“TEMP_SUP”,
“TEMP_INF”),
COEF_MULT
=
(1., - 1.),
COEF_IMPO
=
0.,
)
It is important to note that with an occurrence of the key word factor
LIAISON_DDL
one corresponds and
only one linear relation.
If one wants to impose the same relation between 2 groups of nodes
GRN01
and
GRN02
(even
temperature node with node for example) one cannot write:
LIAISON_DDL = _F
(GROUP_NO = (GRN01,
GRN02),
DDL
=
(“TEMP”,
“TEMP”),
COEF_MULT
=
(1., - 1.),
COEF_IMPO
=
0.,
)
This writing has direction only if
GRN01
and
GRN02
contain each one one node. It
will be necessary in the case to above clarify each linear relation, node by node.
The key word
LIAISON_GROUP
on the other hand allows to condense the writing of the relations
linear between 2 groups of nodes in opposite.

Code_Aster
®
Version
8.2
Titrate:
Operators
AFFE_CHAR_THER
and
THER_F
Date:
22/02/06
Author (S):
X. DESROCHES
Key
:
U4.44.02-I1
Page
:
18/28
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
4.11 Key word
LIAISON_GROUP
4.11.1 Drank
Key word factor usable to define linear relations between couples of nodes, these couples
nodes being obtained while putting in opposite two lists of meshs or nodes.
According to the name of the operator called, the values are provided directly (
AFFE_CHAR_THER
) or
via a concept
function
(
AFFE_CHAR_THER_F
).
4.11.2 Syntax
·
for
AFFE_CHAR_THER
LIAISON_GROUP=_F
(
/
/
MAILLE_1 = lma1, [l_maille]
/
GROUP_MA_1 =
lgma1,
[l_gr_maille]
/
MAILLE_2 = lma2, [l_maille]
/
GROUP_MA_2 =
lgma2,
[l_gr_maille]
/
/
NOEUD_1 = lno1,
[l_noeud]
/
GROUP_NO_1 =
lgno1,
[l_gr_noeud]
/
NOEUD_2 = lno2,
[l_noeud]
/
GROUP_NO_2 =
lgno2,
[l_gr_noeud]
/
SANS_NOEUD =
lno, [l_noeud]
/
SANS_GROUP_NO
=
lgno,
[l_gr_noeud]
DDL_1 =
|
“TEMP”, [DEFECT]
|
“TEMP_INF”,
|
“TEMP_SUP”,
DDL_2 =
|
“TEMP”, [DEFECT]
|
“TEMP_INF”,
|
“TEMP_SUP”,
COEF_MULT_1 =
1i
,
[l_R]
COEF_MULT_2 =
2i
,
[l_R]
COEF_IMPO
=
,
[R]
|
CENTER
=
Lr
,
[l_R]
|
ANGL_NAUT
=
Lr
,
[l_R]
|
TRAN =
Lr
,
[l_R]
SUMMIT
=
“YES”,
)
Code_Aster
®
Version
8.2
Titrate:
Operators
AFFE_CHAR_THER
and
THER_F
Date:
22/02/06
Author (S):
X. DESROCHES
Key
:
U4.44.02-I1
Page
:
19/28
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
·
for
AFFE_CHAR_THER_F
LIAISON_GROUP=_F
(
/
/
MAILLE_1 = lma1, [l_maille]
/
GROUP_MA_1 =
lgma1,
[l_gr_maille]
/
MAILLE_2 = lma2, [l_maille]
/
GROUP_MA_2 =
lgma2,
[l_gr_maille]
/
/
NOEUD_1 = lno1,
[l_noeud]
/
GROUP_NO_1 =
lgno1,
[l_gr_noeud]
/
NOEUD_2 = lno2,
[l_noeud]
/
GROUP_NO_2 =
lgno2,
[l_gr_noeud]
/
SANS_NOEUD =
lno, [l_noeud]
/
SANS_GROUP_NO
=
lgno,
[l_gr_noeud]
DDL_1 =
|
“TEMP”, [DEFECT]
|
“TEMP_INF”,
|
“TEMP_SUP”,
DDL_2 =
|
“TEMP”, [DEFECT]
|
“TEMP_INF”,
|
“TEMP_SUP”,
COEF_MULT_1 =
1i
,
[l_R]
COEF_MULT_2 =
2i
,
[l_R]
COEF_IMPO
=
F
,
[function]
|
CENTER
=
Lr
,
[l_R]
|
ANGL_NAUT
=
Lr
,
[l_R]
|
TRAN =
Lr
,
[l_R]
SUMMIT
=
“YES”
)
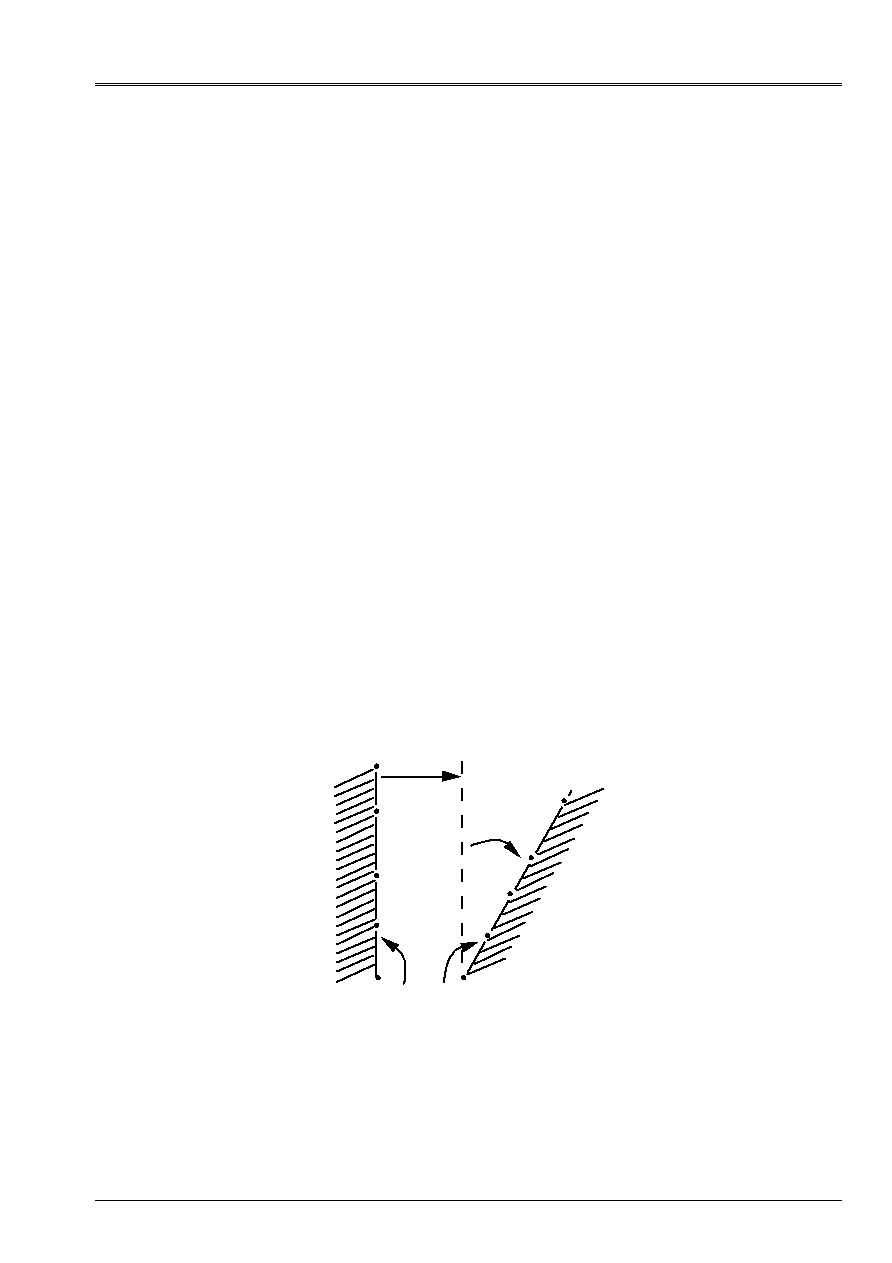
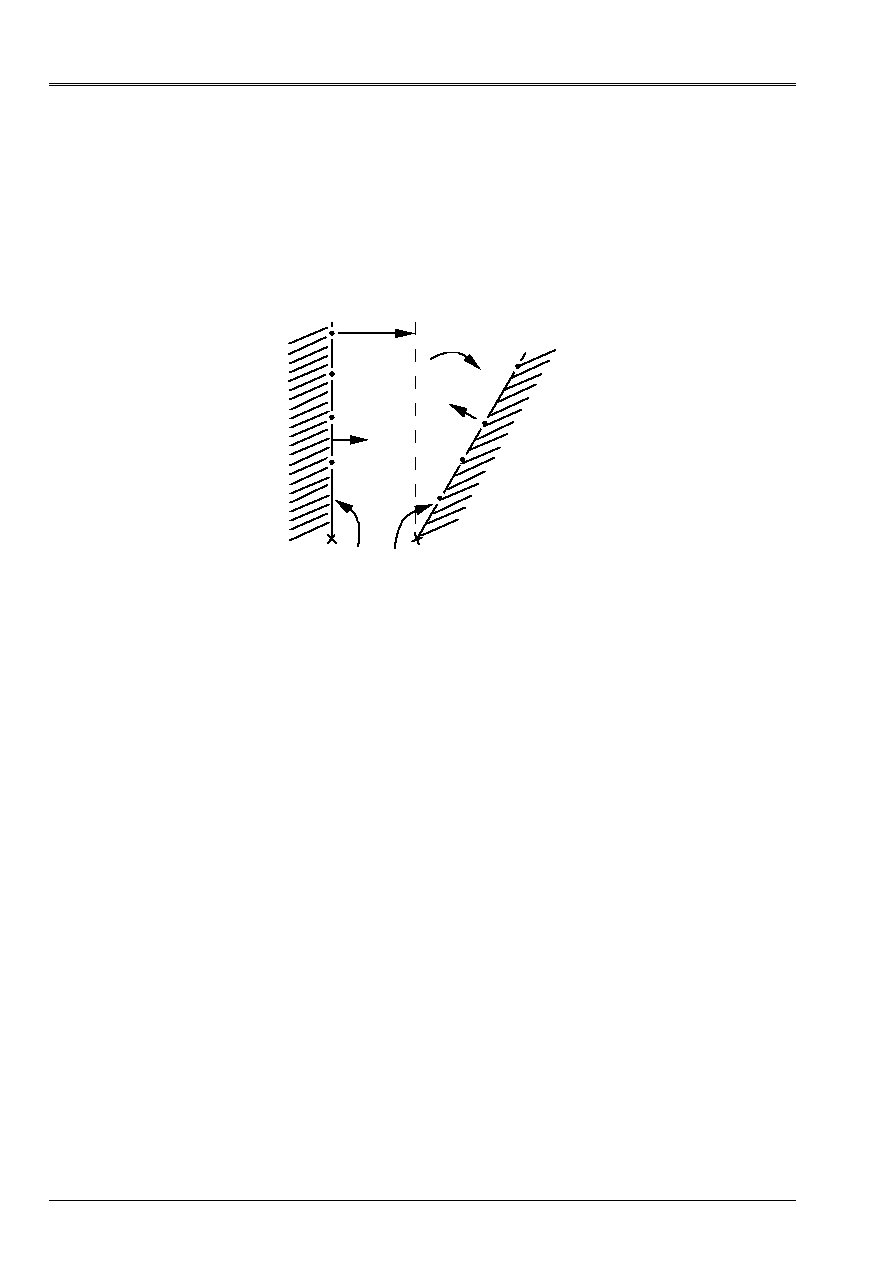
4.11.3 Operands
1
2
T
O
Appear geometrical 4.11.3-a: Transformation
of a border in another

Code_Aster
®
Version
8.2
Titrate:
Operators
AFFE_CHAR_THER
and
THER_F
Date:
22/02/06
Author (S):
X. DESROCHES
Key
:
U4.44.02-I1
Page
:
20/28
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
Kinematic condition “general”:
/
/MAILLE_1
=
/
GROUP_MA_1
=
These operands define
via the meshs which make it up.
/MAILLE_2
=
/
GROUP_MA_2
=
These operands define
2
via the meshs which make it up.
/
/NOEUD_1
=
/
GROUP_NO_1
=
These operands define
via the nodes which make it up.
/NOEUD_2
=
/
GROUP_NO_2
=
These operands define
2
via the nodes which make it up.
/SANS_GROUP_NO
=:
/
SANS_NOEUD
=
These operands make it possible to remove list of the couples of nodes in opposite all
the couples of which at least one of the nodes belongs to the list of nodes described by these
operands.
That makes it possible to avoid the accumulation of linear relations on the same node during
various iterations on the key word factor
LIAISON_GROUP
what leads the majority of
time with a singular matrix.
COEF_MULT_1 (
resp.
COEF_MULT_2)
List realities dimensioned exactly with the number of degrees of freedom declared in
DDL_1
(resp.
DDL_2
) corresponding to the multiplying coefficients of the linear relation.
COEF_IMPO:
coefficient of blocking of the linear relation:
: reality
for
AFFE_CHAR_THER
F
: function
for
AFFE_CHAR_THER_F
CENTER
:
co-ordinates of the center of rotation
ANGL_NAUT
:
nautical angles in degrees defining rotation (see AFFE_CARA_ELEM
[U4.42.01] key word ORIENTATION)
TRAN:
components of the vector translation
These operands make it possible to define a virtual transformation (rotation and/or translation)
approximate of
1
in
2
in order to ensure the bijectivity of the function opposite.
DDL_1
(
resp.
DDL_2):
List texts taken among:
“TEMP”, “TEMP_INF”, “TEMP_SUP”
“TEMP_INF”
and
“TEMP_SUP”
can be used only for elements of hull
thermics (modeling:
“HULL”
).
By defect, the degree of freedom considered for all the nodes of the linear relations is
“TEMP”
.

Code_Aster
®
Version
8.2
Titrate:
Operators
AFFE_CHAR_THER
and
THER_F
Date:
22/02/06
Author (S):
X. DESROCHES
Key
:
U4.44.02-I1
Page
:
21/28
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
SUMMIT = “YES”
When the meshs of edge are quadratic, the use of
SUMMIT: “YES”
force
the algorithm of pairing to associate the nodes nodes other nodes nodes. In
the case of fine mesh, that makes it possible in certain cases to avoid the problems of conflicts of
opposite.
4.11.4 Use of
LIAISON_GROUP
·
LIAISON_GROUP
generate linear relations only between 2 nodes (one on
1
, one on
2
)
To generate linear relations on more than 2 nodes, to use the key word
LIAISON_DDL
.
·
determination of the couples of nodes in opposite:
initially, one draws up the two lists of nodes to be put in opposite (IE at
to pair), for each occurrence of the key word factor
LIAISON_GROUP
:
·
for the key words
GROUP_NO_1
and
GROUP_NO_2
, they are the nodes constituting them
groups of nodes,
·
for the key words
GROUP_MA_1
and
GROUP_MA_2
, they are the nodes of the meshs
setting up the groups of meshs.
The redundancies being eliminated, the two lists of nodes obtained must have the same one
length.
The determination of the couples of nodes in opposite is done in several stages:
·
for each N1 node of the first list, one seeks the node image N2 = F (N1) of
second list. If F is not injective (a node N2 is the image of two distinct nodes
N1 and N1'), the error message according to is transmitted:
<F> <AFFE_CHAR_THER> <PACOAP> CONFLICT IN OPPOSITE
NODES
THE NODE N2 EAST IT WITH RESPECT TO THE NODES N1 AND N1'
·
for each node N2 of the second list, one seeks the node N1 image = G (N2) of
first list. If G is not injective (a N1 node is the image of two distinct nodes
N2 and N2'), the error message according to is transmitted:
<F> <AFFE_CHAR_MECA> <PACOAP> CONFLICT IN OPPOSITE
NODES
THE NODE N1 EAST IT WITH RESPECT TO THE NODES N2 AND N2'
·
it is checked that G = F
1
, i.e. the couples obtained by the stages has) and b) are them
same (one wants to have a bijection F between the two lists of nodes). If F is not
surjective, the error message according to is transmitted:
<F> <AFFE_CHAR_MECA> <PACOAP> CONFLICT IN OPPOSITE GENERATE
SUCCESSIVELY FROM LISTS LIST1 AND LIST2
The NODE OF the FIRST N1 LIST IS NOT the IMAGE Of ANY NODE BY
CORRESPONDENCE
OPPOSITE
For a node NR given, one calls node image F (NR) the node of the other list of nodes which
carry out the minimum of the distance with NR. to facilitate pairing, in particular in the case
particular geometries (where borders
1
and
2
could “almost” result one from
the other by the composition of a translation and a rotation), one makes it possible to make
a virtual geometrical transformation of the first group of nodes (translation and rotation
(cf [Figure 4.11.3-a]) before calculating the distances (key words
TRAN
,
CENTER
and
ANGL_NAUT
).
For each occurrence of the key word factor
LIAISON_GROUP
, one builds the list thus of
new couples in opposite. When all the occurrences were swept, one removes
list the couples in double.

Code_Aster
®
Version
8.2
Titrate:
Operators
AFFE_CHAR_THER
and
THER_F
Date:
22/02/06
Author (S):
X. DESROCHES
Key
:
U4.44.02-I1
Page
:
22/28
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
Note:
In the couples of nodes in opposite, the command of the nodes is important. If for
first occurrence of
LIAISON_GROUP
, a node NR belonged to the first group of
nodes and a node M with the second group of nodes, and that for the second occurrence
of
LIAISON_GROUP
, it is the reverse, one will obtain with the exit pairing the couples (NR,
M) and (M, NR). They will not be eliminated during detection of the redundancies; on the other hand,
stamp obtained will be singular. Thus, one advises to keep same logic at the time of
description of the edges in opposite.
4.12 Key word
LIAISON_MAIL
4.12.1 Drank
Key word factor allowing “to thermically restick” two edges of a structure. These edges can
to be with a grid differently (incompatible mesh) but must result one from the other by rotation
and/or translation.
4.12.2 Syntax
·
in
AFFE_CHAR_THER
only
LIAISON_MAIL
=_F
(
|
GROUP_MA_MAIT
=
lgma_mait,
|
MAILLE_MAIT =
lma_mait,
|
GROUP_MA_ESCL
=
lgma_escl,
|
MAILLE_ESCL =
lma_escl,
|
GROUP_NO_ESCL
=
lgno_escl,
|
NOEUD_ESCL =
lno_escl,
|
TRAN =
(tx, ty, [tz]),
[l_R]
|
CENTER =
(teststemxç, teststemyç, [zc]),
[l_R]
ANGL_NAUT = (alpha, [beta, gamma]),
[l_R]
)
Face 1 is called face “Master”, face 2 face “slave”.
4.12.3 Operands
4.12.3.1 GROUP_MA_ESCL/MAILLE_ESCL/GROUP_NO_ESCL/NOEUD_ESCL
These key words make it possible to define the whole of the nodes of the face slave. One takes all them
nodes specified by key words GROUP_NO_ESCL and NOEUD_ESCL more possibly nodes
carried by the meshs specified by key words GROUP_MA_ESCL and MAILLE_ESCL.
4.12.3.2 GROUP_MA_MAIT/MAILLE_MAIT
These key words make it possible to define the whole of the meshs where they with respect to the nodes will be sought
face slave.
One should not give the meshs of surface (in 3D) composing the face Master, but the meshs
voluminal adjacent with the face Master. The specified meshs are candidates for search
opposite. One can give too much of it.

Code_Aster
®
Version
8.2
Titrate:
Operators
AFFE_CHAR_THER
and
THER_F
Date:
22/02/06
Author (S):
X. DESROCHES
Key
:
U4.44.02-I1
Page
:
23/28
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
4.12.3.3 CENTER/ANGL_NAUT/TRAN
These operands make it possible to define the geometrical transformation (rotation and/or translation)
allowing to pass from the face main slave to the face. The control carries out initially rotation
then translation.
Caution: the transformation is in the direction slave-Master.
This boundary condition applies to plane modelings (“PLAN” or “AXIS”) or voluminal
(“3D”).
4.13 Key word
ECHANGE_PAROI
4.13.1 Drank
Key word factor usable to apply conditions of heat exchange between 2 definite walls
each one by one or more meshs or one or more groups of meshs.
4.13.2 Syntax
·
for
AFFE_CHAR_THER
ECHANGE_PAROI=_F
(
/
GROUP_MA_1
=
lgma,
[l_gr_maille]
/
MAILLE_1
= lma, [l_maille]
/
GROUP_MA_2
=
lgma,
[l_gr_maille]
/
MAILLE_2
= lma, [l_maille]
COEF_H
=
H,
[R]
|
TRAN
=
Lr,
[l_R]
|
ANGL_NAUT
=
Lr,
[l_R]
|
CENTER
=
Lr,
[l_R]
)
·
for
AFFE_CHAR_THER_F
ECHANGE_PAROI=_F
(
/
GROUP_MA_1
=
lgma,
[l_gr_maille]
/
MAILLE_1
= lma, [l_maille]
/
GROUP_MA_2
=
lgma,
[l_gr_maille]
/
MAILLE_2
= lma, [l_maille]
COEF_H
=
HF,
[function]
|
TRAN
=
Lr
,
[l_R]
|
ANGL_NAUT
=
Lr
,
[l_R]
|
CENTER
=
Lr
,
[l_R]
)
Code_Aster
®
Version
8.2
Titrate:
Operators
AFFE_CHAR_THER
and
THER_F
Date:
22/02/06
Author (S):
X. DESROCHES
Key
:
U4.44.02-I1
Page
:
24/28
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
4.13.3 Operands
/GROUP_MA_1
/
MAILLE_1
/GROUP_MA_2
/
MAILLE_2
1
2
T
N
2
N
1
O
Appear 4.13.3-a
These operands make it possible to define the 2 lists of meshs representing for the list
subscripted _1 the wall
1
for the subscripted list _2 the wall
2
.
The walls are in correspondence and must comprise the same number of meshs and
nodes.
The limiting condition applied between these 2 walls is:
F representing the bijection which puts in opposite a node of
1
and a node of
2
.
/COEF_H
=
Coefficient of constant exchange enters the 2 walls:
reality for the operator
AFFE_CHAR_THER
, function for the operator
AFFE_CHAR_THER_F
.
|
TRAN =
components of the vector translation
|
ANGL_NAUT
=
nautical angles defining rotation
|
CENTER
=
co-ordinates of the center of rotation
These operands make it possible to define a virtual transformation (rotation and/or translation)
approximate of
1
in
2
in order to ensure the bijectivity of the function in opposite.
Code_Aster
®
Version
8.2
Titrate:
Operators
AFFE_CHAR_THER
and
THER_F
Date:
22/02/06
Author (S):
X. DESROCHES
Key
:
U4.44.02-I1
Page
:
25/28
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
TRAN
:
characterize a translation
T
in 2D one thus has
:
TRAN =
(tx, ty)
in 3D one has
:
TRAN =
(tx, ty, tz)
ANGL_NAUT
:
nautical angle allowing to define a rotation
in 2D
:
1 angle
in 3D
:
3 angles (cf [U4.42.01])
CENTER
:
center of rotation
in 2D
:
(OX, OY)
in 3D
:
(OX, OY, OZ)
4.13.4 Use of
ECHANGE_PAROI
The user gives two lists of meshs from which the couples from paired nodes will result. These lists
are initially sorted by type of mesh: the paired nodes will come from meshs of the identical type.
For each mesh of the first list, one determines the mesh nearest in the second list
by calculating all the distances from the nodes taken two to two (one traverses all the permutations
possible). The distance minimum obtained defines at the same time the mesh in opposite and the couples of
nodes paired for the two meshs concerned. As in
LIAISON_GROUP
[§4.11], it is
possible to carry out a virtual geometrical transformation (rotation and/or translation) before
to calculate the distances.
4.13.5 Meshs and modelings supporting this loading:
Net edge
Modeling
Net coupling generated
SEG2, SEG3
PLAN, PLAN_DIAG
AXIS, AXIS_DIAG
SEG22, SEG33
TRIA3, TRIA6,
QUAD4, QUAD8, QUAD9
3D, 3d_DIAG
TRIA33, TRIA66,
QUAD44, QUAD88, QUAD99

Code_Aster
®
Version
8.2
Titrate:
Operators
AFFE_CHAR_THER
and
THER_F
Date:
22/02/06
Author (S):
X. DESROCHES
Key
:
U4.44.02-I1
Page
:
26/28
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
4.14 Key word
LIAISON_UNIF
4.14.1 Drank
Key word factor allowing to impose the same value (unknown) on the temperatures of a unit
nodes.
These nodes are defined by the groups of meshs, the meshs, the groups of nodes or the list of
nodes to which they belong.
4.14.2 Syntax
·
for
AFFE_CHAR_THER
and
AFFE_CHAR_THER_F
LIAISON_UNIF
=_F
(
/MESH
= lma
,
[l_maille]
/
GROUP_MA
=
lgma,
[l_gr_maille]
/
NODE
=
lno, [l_noeud]
/
GROUP_NO
=
lgno,
[l_gr_noeud]
DDL =
|
“TEMP”
,
[DEFECT]
|
“TEMP_INF”,
|
“TEMP_SUP”,
)
4.14.3 Operands
/MESH
/
GROUP_MA
/
NODE
/
GROUP_NO
These operands make it possible to define a list of nodes
from which one eliminated them
redundancies (for
NET
and
GROUP_MA
, they are connectivities of the meshs).
DDL
This operand makes it possible to define a list of degrees of freedom
texts taken
among:
“TEMP”
,
“TEMP_INF”
,
“TEMP_SUP”
.
conditions “kinematics” resulting are:
Note:
Components
“TEMP_SUP”
,
“TEMP_INF”
can intervene only for nodes
elements of hull.

Code_Aster
®
Version
8.2
Titrate:
Operators
AFFE_CHAR_THER
and
THER_F
Date:
22/02/06
Author (S):
X. DESROCHES
Key
:
U4.44.02-I1
Page
:
27/28
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
4.15 Key word
LIAISON_CHAMNO
4.15.1 Drank
Key word factor usable to define a linear relation between all the temperatures present
in a concept
CHAM_NO
.
4.15.2 Syntax
LIAISON_CHAMNO = _F (
CHAM_NO = chamno,
[cham_no]
COEF_IMPO =
,
[R]
NUME_LAGR
=
/
“NORMAL”,
[DEFECT]
/
“AFTER”
,
)
4.15.3 Operands
CHAM_NO =
Name of
chamno
who is used to define the linear relation. The temperatures connected are all those
present in
chamno
. The coefficients to be applied to the temperatures are the values of these
temperatures in
chamno
.
Example:
Let us suppose that one has one
chamno
relating to 3 nodes of name N01, N02 and N03.
Let us suppose that the values of the temperatures in these 3 nodes in the chamno are
respectively 2., 5.4 and 9.1. The linear relation that one will impose is 2.* Temp (N01) +
5.4 * temp (N02) + 9.1 * temp (N03) =
COEF_IMPO =
It is the value of the real coefficient
with the second member of the linear relation.
NUME_LAGR =
If
“NORMAL”
, the 2 multipliers of Lagrange associated with the relation will be such as the first will be
located before all the terms implied in the relation and the second after, in the assembled matrix.
If
“AFTER”
, the 2 multipliers of Lagrange associated with the relation will be located after all them
terms implied in the relation, the assembled matrix.
This choice has the advantage of having an assembled matrix whose overall dimension is weaker but
has the disadvantage to be able to reveal a singularity in the matrix.

Code_Aster
®
Version
8.2
Titrate:
Operators
AFFE_CHAR_THER
and
THER_F
Date:
22/02/06
Author (S):
X. DESROCHES
Key
:
U4.44.02-I1
Page
:
28/28
Instruction manual
U4.4- booklet: Modeling
HT-62/06/004/A
4.16 Key word
CONVECTION
4.16.1 Drank
Key word usable to take into account the term of transport of heat by convection of which
the expression is
, appearing in the expression of the particulate derivative
.
In the case of a liquid medium,
V
indicate the speed imposed of the fluid particle on the current point.
In the case of a mobile solid medium,
V
indicate the speed of the solid. In all the cases, one supposes
that the field speed is known a priori. The case of a mobile solid is rather frequent in practice. It
relate to in particular the applications of welding or surface treatment which bring into play one
heat source moving in a given direction and at a speed.
The thermal problem is then studied in a reference frame related to the source (cf THER_NON_LINE_MO
[U4.54.03]).
4.16.2 Syntax
CONVECTION = _F (
SPEED
=
v
[cham_no_depl_R])
4.16.3 Operand
For
AFFE_CHAR_THER
and
AFFE_CHAR_THER_F
,
SPEED =
Name of the field speed at the moment when calculation is carried out.
This field is a concept
cham_no
of type
cham_no_depl_R
. It must have been defined on all it
model for which one carries out calculation.




























