PROPERTIES OF THE ATMOSPHERE
SOFTWARE DOWNLOADS
1. International Standard Atmosphere
1.1 Sea Level Conditions
Pressure	101.3 kPa	2116.7 lbf/ft2
Density	1.225 Kg/m3	0.002378 slug/ft3
Temperature	15oC or 288.2 K	59oF or 518 R
Speed of Sound	340.3 m/s	1116.4 ft/s
Viscosity	1.789 x 10-5 Kg/m/s	3.737 x 10-7 slug/ft/s
Kinematic Viscosity	1.460x10-5 m2/s	1.5723x10-4 ft2/s
Thermal Conductivity	0.02596 W/m/K	0.015 BTU/hr/ft/oR
Gas Constant	287.1 J/Kg/K	1715.7 ft lbf/slug/oR
Specific Heat Cp	1005 J/Kg/K	6005 ft lbf/slug/oR
Specific Heat Cv	717.98 J/Kg/K	4289 ft lbf/slug/oR
Ratio of Specific Heats	1.40
Gravitational Acceleration	9.80665 m/s2	32.174 ft/s2

1.2 Variation with Altitude

Figure 1 : Atmospheric temperature at different altitudes Figure 2 : Troposphere and Stratosphere Pressure, temperature, density, viscosity and speed of sound variation for the international standard atmosphere (ISA) can be calculated for a range of altitudes from sea level upward. This is done using an exact solution to the hydrostatic equation for a column of air. The air is assumed to be a perfect gas. In the lower region, the troposphere, the atmosphere has a lapse rate (L) of 6.5K/Km. At an altitude of 36089 ft the stratosphere starts and the temperature remains constant at 217K. The hydrostatic equation, perfect gas law and the lapse rate equation are

where the variables used are P -- Pressure (Pa); T -- Temperature (K); -- Density (Kg/m3); g -- Gravitational acceleration (9.8 m/s2); To -- Standard sea level temperature (288 K); R -- Gas constant for air (287 m2/s2/K); h -- Altitude above sea level (m) and L -- Lapse rate (0.0065 K/m). Solving the hydrostatic equation with a constant lapse rate gives the resulting pressure variation in the troposphere. where Po is set at 101.3 kPa. Solving the hydrostatic equation with a constant temperature gives the resulting pressure variation in the stratosphere. where conditions with subscript (s) are values of altitude (hs), pressure (Ps) or temperature (Ts) at the tropopause, the start of the stratosphere, the line dividing the two distinct atmospheric regions. Once pressure has been calculated at a particular altitude, density is then calculated using the perfect gas law. Viscosity and kinematic viscosity are found by applying the Sutherland law And finally speed of sound is found as where is the Ratio of Specific Heats for air and is equal to 1.4

Based on the above equations, an application is available which shows atmospheric properties for a specific altitude. This application can also be used to predict Mach Number, Dynamic Pressure and other altitude dependent properties if an input speed and reference length are given.

Application : International Standard Atmosphere Calculator Data : International Standard Atmosphere Tabulated Data

2. Correction for Air Density due to Humidity

The density of the air for a given level of humidity can be found by applying a correction factor to the above calculated perfect gas density.

The correction factor, Kh, can be found by using wet and dry bulb temperature measurements to predict relative humidity as shown in the following table.

Relative Humidity (%)
Dry Bulb oC	Temperature Difference,oC TDRY - TWET 1 2 3 4 5 6 7 8 9 10 11 12
0	81 64 46 29 13 - - - - - - -
2	84 68 52 37 22 7 - - - - - -
4	85 71 57 43 29 16 - - - - - -
6	86 73 60 48 35 24 11 - - - - -
8	87 75 63 51 40 29 19 8 - - - -
10	88 77 66 55 44 34 24 15 6 - - -
12	89 78 68 58 48 39 29 21 12 - - -
14	90 79 70 60 51 42 34 26 18 10 - -
16	90 81 71 63 54 46 38 30 23 15 8 -
18	91 82 73 65 57 49 41 34 27 20 14 7
20	91 83 74 66 59 51 44 37 31 24 18 12
22	92 83 76 68 61 54 47 40 34 28 22 17
24	92 84 77 69 62 56 49 43 37 31 26 20
26	92 85 78 71 64 58 51 46 40 34 29 24
28	93 85 78 72 65 59 53 48 42 37 32 27
30	93 86 79 73 67 61 55 50 44 39 35 30
32	93 86 80 74 68 62 57 51 46 41 37 32
34	93 87 81 75 69 63 58 53 48 43 39 35
36	94 87 81 75 70 64 59 54 50 45 41 37

---

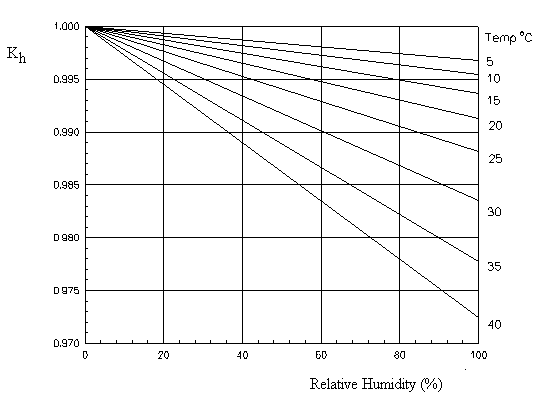
The relative humidity can be used to obtain the density correction factor from the following graph.

Density Correction due to Humidity