|
The theorem we have stated is a very general one, but by no means
limited to Fluid Mechanics. It is used in diversified fields such
as Botany and Social Sciences and books and volumes have been
written on this topic. But we do not need much theory to be able
to apply it. What we will consider is a procedure to use the
theorem and arrive at non-dimensional numbers for a given flow.
- List all the variables that govern the process. These
variables should be independent of each other. For example,
one should not choose density, gravity and specific weight.
Density and Specific Weight should do. For our problem we have F, D, V,
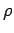 and and 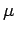 . We have n = 5. . We have n = 5.
- Mark the Repeating variables. In our case these are D, V and
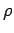 making k = 3 . making k = 3 .
- Decide how many non-dimensional numbers are there. For
our case we have n - k = 2. Our problem has 2 non-dimensional numbers,
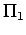 and and
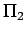 . .
- Define the non-dimensional numbers by grouping the
variables into n - k groups so that each group has all the
repeating variables and one non-repeating variable. Thus for
our problem we have
- Now express each variables in terms of its dimensions. Let
us use the MLT system according to which the variables for our
problems have the following dimensions.
| Variable |
Dimensions |
| F, Force |
M L / T2 or
M L T-2 |
| D, Diameter: |
L |
| V, Velocity |
L/T or LT-1 |
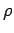 , Density: , Density: |
M/L3 or ML-3 |
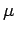 , Viscosity , Viscosity |
ML-1T-1 |
Substituting these dimensions into Eqn. 5.2, we have
Noting that 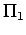 and and 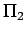 are non-dimensional we have, are non-dimensional we have,
| a + b - 3c + 1 = 0; -b - 2 = 0, c + 1 = 0 |
|
| e + f - 3g - 1 = 0; -f - 1 = 0;g + 1 = 0 |
(5.6) |
Solving the equations yields,
| a = -2, b = -2, c = -1 |
|
| e = -1, f = -1, g = -1 |
(5.7) |
Now our non-dimensional numbers become,
Thus we have found the non-dimensional numbers for the flow of
interest, namely, drag about a circular cylinder. The functional
relationship between the two numbers may be expressed as
But note that the form of term 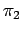 we have derived is somewhat
different from what we assumed at the beginning. The right hand
side of the equation is actually the inverse of Reynolds number!
This points to the drawback of the analysis that the exact
functional form between the we have derived is somewhat
different from what we assumed at the beginning. The right hand
side of the equation is actually the inverse of Reynolds number!
This points to the drawback of the analysis that the exact
functional form between the 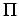 numbers cannot be obtained. Any
coefficient or index obtained cannot be determined by this
analysis. This should be determined by experimentation or by
computations. But since the numbers are non-dimensional we can
always write, numbers cannot be obtained. Any
coefficient or index obtained cannot be determined by this
analysis. This should be determined by experimentation or by
computations. But since the numbers are non-dimensional we can
always write,
(c) Aerospace, Mechanical & Mechatronic Engg. 2005
University of Sydney
|

