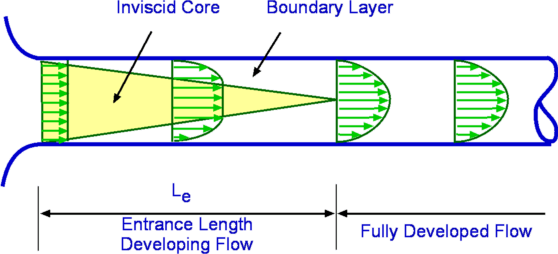
Figure 7.4: Flow at the entrance to a pipe
Consider a flow entering a pipe. Let us think of the entering flow
being uniform, so inviscid. As soon as the flow 'hits' the pipe
many changes take place. The most important of these is that
viscosity imposes itself on the flow and the "No Slip" condition
at the wall of the pipe comes into effect. Consequently the
velocity components are each zero on the wall, ie., u = v = 0. The
flow adjacent to the wall decelerates continuously. We have a
layer close to the body where the velocity builds up slowly from
zero at wall to a uniform velocity towards the center of the pipe.
This layer is what is called the Boundary Layer. Viscous effects
are dominant within the boundary layer. Outside of this layer is
the inviscid core where viscous effects are negligible or absent.
The boundary layer is not a static phenomenon; it is dynamic. it
grows meaning that its thickness increases as we move downstream.
From Fig. it is seen that the boundary layer from the walls grows
to such an extent that they all merge on the centreline of the
pipe. Once this takes place, inviscid core terminates and the flow
is all viscous. The flow is now called a Fully Developed
Flow. The velocity profile becomes parabolic. Once the flow is
fully developed the velocity profile does not vary in the flow
direction. In fact in this region the pressure gradient and the
shear stress in the flow are in balance. The length of the pipe
between the start and the point where the fully developed flow
begins is called the Entrance Length. Denoted by Le, the
entrance length is a function of the Reynolds Number of the flow.
In general,
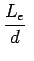 |
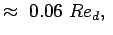 for a Laminar Flow for a Laminar Flow |
(7.1) |
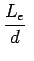 |
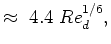 for a Turbulent Flow for a Turbulent Flow |
(7.2) |
At critical condition, i.e.,
Red =2300, the Le/d for a
laminar flow is 138. Under turbulent conditions it ranges from 18(at Red = 4000) to 95 (at
Red=108)
Application decides whether a long enough entrance length is
required or a shorter one is required. Take wind tunnel for
instance. Here the aim is to have a uniform flow over the model in
the test section. So one desires to have a longer entrance length.
Subsections
(c) Aerospace, Mechanical & Mechatronic Engg. 2005
University of Sydney
|

