| Translation is the type of motion where the element retains its shape. Its side do not undergo any change in length and the four angles do remain square. The square element ABCD, we have considered is bodily shifted from its position to a new one A`B`C`D`. If the motion is without acceleration in a steady, uniform flow it is easy to calculate the position of any particle in the fluid at different instants of time. But it should be noted that the fluid particles may undergo acceleration. |
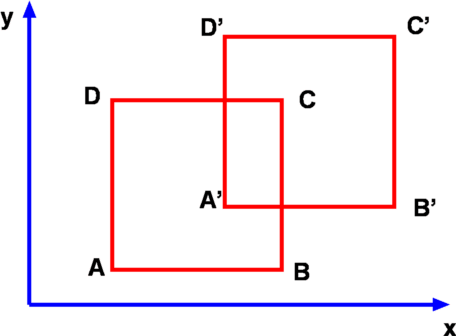
Figure 4.7: Translation of A fluid Element |
Considering now a particle in the fluid element we can write down
an expression for its acceleration. At time t, the particle is
at (x,y,z) and its velocity is given by,
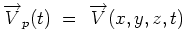 |
(4.25) |
where
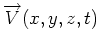 is the fluid velocity. At time
(t+dt) the particle will find itself at a different location and
its velocity now is given by, is the fluid velocity. At time
(t+dt) the particle will find itself at a different location and
its velocity now is given by,
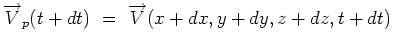 |
(4.26) |
Consequently the change in velocity is given by,
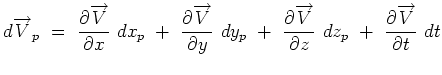 |
(4.27) |
The acceleration of the particle is obtained by dividing
throughout by dt. Accordingly,
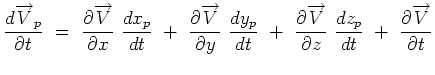 |
(4.28) |
Now denoting the speed in x-direction, dx/dt by u, speed in
y-direction dy/dt by v and speed in z-direction dz/dt by w, we
have,
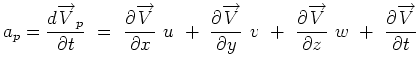 |
(4.29) |
where ap is the particle acceleration. The derivative dVp/dt is usually denoted by DV/Dt and is called Material
Derivative or the Particle Derivative or the Total Derivative.
(c) Aerospace, Mechanical & Mechatronic Engg. 2005
University of Sydney
|

