|
Consider a radial flow going away from the origin at a velocity
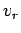 as shown in Fig.4.19. This constitutes a Source
Flow. This is a purely radial flow with no component of velocity
in the tangential direction, i.e., as shown in Fig.4.19. This constitutes a Source
Flow. This is a purely radial flow with no component of velocity
in the tangential direction, i.e.,
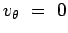 . If m is the
volumetric flow rate we have . If m is the
volumetric flow rate we have
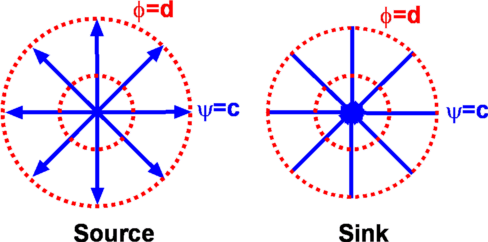
Figure 4.19: Source Flow and Sink Flow.
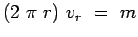 |
|
i.e., 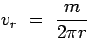 |
(4.74) |
We can now write down velocity potential and stream function for
this flow -
It is easily verified that
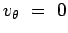 for this flow. Further,
the equation we started out with , namely, Eqn.4.74 is
the continuity equation for the source flow. It states that the
Volumetric flow rate (mass flow rate when multiplied by density)
is constant in a radial direction and is equal to m, which is
called the Strength of the source. for this flow. Further,
the equation we started out with , namely, Eqn.4.74 is
the continuity equation for the source flow. It states that the
Volumetric flow rate (mass flow rate when multiplied by density)
is constant in a radial direction and is equal to m, which is
called the Strength of the source.
Another point to make is that the radial velocity 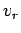 becomes
infinite at r = 0. So the origin is a singularity of the flow. becomes
infinite at r = 0. So the origin is a singularity of the flow.
If m is negative we have a flow which flows inwards and is
called a Sink flow, which again has a singularity at the
origin.
(c) Aerospace, Mechanical & Mechatronic Engg. 2005
University of Sydney
| 
