|
The stagnation points we saw in Fig. 4.33 are for the
case when the circulation imposed on the cylinder was such that
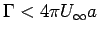 . But from Eqn. 4.131 it is
evident that angle . But from Eqn. 4.131 it is
evident that angle 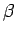 , hence the position of the stagnation
points is a strong function of circulation, , hence the position of the stagnation
points is a strong function of circulation, 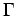 . This is
illustrated in Fig.4.34. With zero circulation the
stagnation points lie at . This is
illustrated in Fig.4.34. With zero circulation the
stagnation points lie at 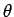 = o, = o, 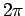 . As circulation . As circulation
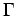 increases the stagnation points move (upwards or
downwards depending upon the direction of rotation). When increases the stagnation points move (upwards or
downwards depending upon the direction of rotation). When
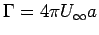 they coincide at they coincide at 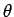 = =
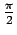 or or
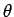 = - = -
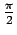 . If circulation is further increased
the stagnation point will no longer be found on the cylinder
surface, but will appear in the flow as shown in D in Fig.
4.34. . If circulation is further increased
the stagnation point will no longer be found on the cylinder
surface, but will appear in the flow as shown in D in Fig.
4.34.
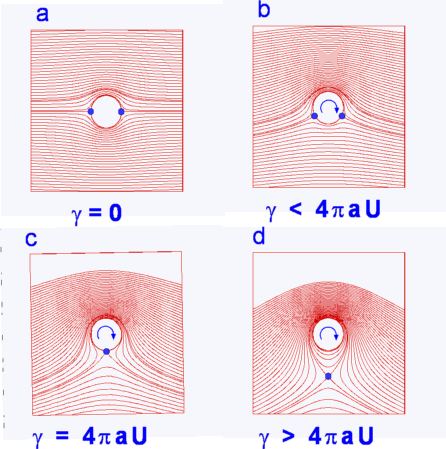
Figure 4.34: Effect of circulation on flow about a cylinder
(c) Aerospace, Mechanical & Mechatronic Engg. 2005
University of Sydney
|

