 Prandtl Lifting Line Theory (3-D Potential Flow) |
|
SOFTWARE DOWNLOADS |
|
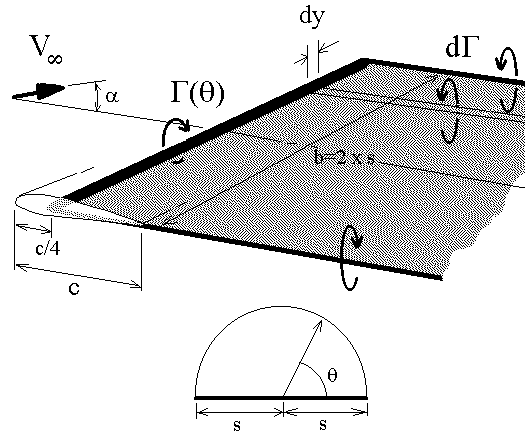
A simple solution for unswept three-dimensional wings can be obtained by using Prandtl's lifting line model. For incompressible, inviscid flow, the wing is modelled as a single bound vortex line located at the 1/4 chord position and an associated shed vortex sheet.
The span-wise lift distribution is assumed to be elliptical with a small modification due to wing planform geometry. The assumed vortex line strength is thus a Fourier series approximation.
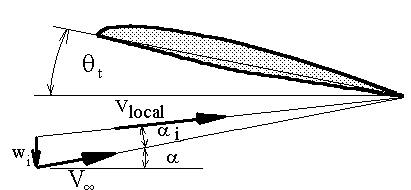
The required strength of the distribution coefficients (An) for a given geometry and set of freestream conditions can be calculated by applying a surface flow boundary condition. The equation used is based on the usual condition of zero flow normal to the surface. For 3-D wings the condition is applied at several span-wise sections by matching flow and surface angles. The local flow angle of incidence for a 2-D section of the wing must be equal to the sum of the wing's angle of attack, the section twist and the downwash induced flow angle. This downwash component is caused by the induced flow from the trailing vortex sheet.
where The vortex strength distribution in the trailing sheet will be a function of the changes in vortex strength along the wing span. The mathematical function describing the vortex sheet strength is thus obtained by differentiating the bound vortex distribution.
A solution for the magnitude of the Fourier coefficients A1,A2,A3... is obtained by firstly predicting the downwash velocity induced on the wing by the trailing sheet.
Then find the 2-D section lift coefficient as a function of the local flow incidence and the bound vortex strength at this span location.
where ao is the section lift curve slope (¶ Cl/¶a ), a o is the zero lift angle and c is the section chord. Rearranging and substituting for the local angle of incidence.
Substituting for G and a i in terms of the Fourier series approximations then a final boundary condition equation is obtained. The equation contains the unknown coefficients and the known geometric properties of the wing.
If a fixed number of coefficients (A1,A2,A3,A4...AN) is used then a set of simultaneous linear equations will be obtained by applying the above equation at "N" spanwise locations. A cosine distribution of spanwise locations should be used to match the assumed wing loading distribution. The number of coefficients used will determine the accuracy of the solution. If the wing loading is highly non-elliptical then a larger number of coefficients should be included. The solution for coefficients (A1,A2,A3,A4...AN) is obtained by the reduction of the resulting matrix of equations. It should be noted that in cases were the wing loading is symmetric then even coefficients (A2,A4,A6,....) will be zero and can be deleted from the calculation. The lift coefficient for the wing at a given angle of attack will be obtained by integrating the spanwise vortex distribution.
so that The downwash velocity induced at any span location can be calculated once the strength of the wing loading is known. The variation in local flow angles can then be found. A consequence of this downwash flow is that the direction of action of each section's lift vector is rotated relative to the freestream direction. The local lift vectors are rotated backward and hence give rise to a lift induced drag. By integrating the component of section lift coefficient that acts parallel to the freestream across the span, the induced drag coefficient can be found.
so that
No real information about pitching moment coefficient can be deduced from lifting line theory since the lift distribution is collapsed to a single line along the 1/4 chord.
Special Case of Elliptical LoadingIf the wing planform is elliptical, then it can be assumed that the wing load distribution is also a purely elliptical function.
In this case a single general boundary condition equation results containing only one unknown, the vortex line strength at the wing root. The exact solution of this equation leads to the following simple answer for lift coefficient and induced drag coefficient.
Prandtl Lifting Line Program The following computer program allows the user to define wing planforms (without sweep) and to define wing root and wing tip section properties. The program assumes a linear variation of section properties between wing root and tip and that the loading will be symmetric about the wing root. The program uses the above lifting line equations to get solutions for lift coefficient versus angle of attack and induced drag coefficient versus lift coefficient2. For a given angle of attack the program will display the resulting distribution of section lift coefficient across the span. A flapped section can also be input. The percentage of wing span with flap must be input to create a flapped wing section. The flap section properties are assumed to be those entered for the wing root section. These section properties will be kept constant across the flapped portion of the span. The section properties used outboard of the flap will also be constant and assumed to be equal to those of the wing tip. SOFTWARE Executable Program : Lifting-Line (3-D) Theory (249k) Reference: "Aerodynamics for Engineering Students" Houghton & Carruthers, Arnold Ed 3 1982. © AMME, University of Sydney, 1998-2006 |
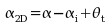
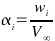
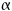 is the 3-D
wing angle of attack,
is the 3-D
wing angle of attack, 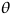 tis the
wing twist angle and wi is the velocity induced by trailing
vortex sheet.
tis the
wing twist angle and wi is the velocity induced by trailing
vortex sheet.
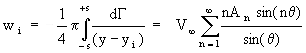
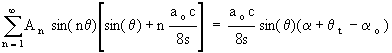
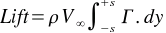
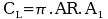 , where AR is wing aspect ratio.
, where AR is wing aspect ratio.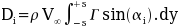
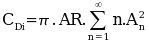
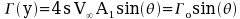
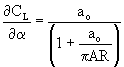 ,
,