Miscellaneous strength topics problems

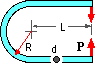
1. A spring is formed by bending a rod of diameter d into a U-shape of radius R and leg length L, where R, L >> d.
   Show that the spring's compliance (reciprocal stiffness) is 32( 4L³ +6πRL² +24R² L +3πR³ )/ 3πEd⁴
    
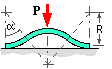2. A spring is made by curving a strip of rectangular cross-section into four identical arcs of radius R and included angle α, as shown. Neglecting friction, show that the deflection, δ, experienced by the load P is :-      δ = ( PR³ /4EI )[ 3( 2α +sin2α ) - 4α cos2α - 8 sinα ]
    
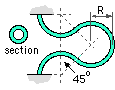3. The flexible pipe loop may be placed between a steam boiler and process plant to reduce the forces caused by thermal expansion of the pipe. Determine the force and moment developed by a temperature rise of T over that at installation. Hint: allow the pipe to expand freely then load it to negate the expansion.
   [ 0.228 EI αT/R² ]
    
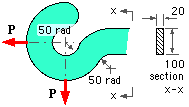4. A hook, of uniform rectangular cross-section and made from a steel whose design stress is 100 MPa, may support a load, P, in either of the two positions shown. What maximum load can the hook sustain ?
   [ 12.6 kN ]
    
5. Find the stresses at the inner and outer surfaces of the trapezoidal section A-A of the riveting frame for a load P of 2 kN.
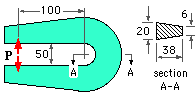
   [ 119 MPa (t), 83 MPa (c) ]
    
    
6. Show that, for a thick curved beam of circular cross-section   2 √ r_d = √ r_i + √ r_o
    
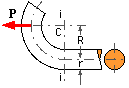7. The end of a straight round rod of radius r is bent to a circular arc of mean radius R. The severity of curvature is characterised by the ratio   λ = r/R.
   The rod supports a force P which acts through the centre of curvature C, normal to the interface i-i between straight and curved portions.
   If   σ_d = P/A is the direct stress, show that the maximum stress is
       σ_d. [λ/(1-λ)] [ 1 +√(1-λ² )] / [ 1 -√(1-λ² )] in a cross-section just to the left of i-i, and
       σ_d. ( 1 + 4 / λ )     in a cross-section just to the right of i-i as sketched.
   Plot these expressions versus   λ   ( 0≤λ≤1 ), comment on the trends displayed, and evaluate the curvature-induced stress concentration for   λ = 0.05, 0.5, 0.95.
   [ 1.04, 1.55, 6.96 ]
    
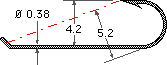8. A fish hook is forged from wire having a yield strength of 2.3 GPa. Assuming a straight pull from the leader through the point, estimate the load which would cause the hook to yield.
   [ 2.2 N ]
    
9. Re-work the derivation of equations ( vi) & ( 4) showing all steps clearly.
    
10. Calculate the centroidal second moments of area of the Z-beam's cross-section. If the components of bending moment at the section illustrated are 50 and 10 kNm about the x- and y-axes respectively, ascertain the safety factor at the section. The material's yield is 250 MPa.
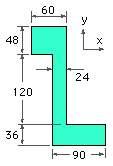
    [ 1.52 ]
     
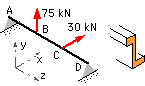11. The beam ABCD, simply supported at A and D and otherwise identical to that above, is loaded by 75 kN at B, in line with the web, and by 30 kN at C parallel to the flanges (AB=BC=CD=1 m). Determine the safety factor.
    [1.12]
     
12. The 10 mm diameter ball end of the steel link is socketed into the 10.1 mm diameter spherical seating of the valve-operating linkage. Properties of materials used in the joint are :

    		steel	bronze	cast iron
    	elastic modulus ( GPa )	207	110	100
    	Poisson's ratio	0.29	0.30	0.21
    	design stress ( MPa )	400	240	100(t), 350(c)

    Determine the maximum allowable linkage force, F, if :
    1. the socket material is bronze and failure occurs due to lubrication breakdown occasioned by the contact pressure exceeding 200 MPa. [ 1.70 kN ]
    2. failure is due to material strength limitations. [ 13.6 kN ]
    3. as (b), but the socket material is cast iron. [ 11.0 kN ]
        
13. A rod passes through a hole of length L and is loaded by a radial force F. Both rod and hole are of nominal diameter d, and the small diametral clearance between them is   c∗d where   c is a fraction. Show that the peak contact pressure is   √( 2cFE*/ πdL ).
     
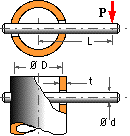14. A wrench, required to produce a torque of 300 Nm, is made from a tube of 50 mm mean diameter and wall thickness t, through which two diametrically opposite holes are drilled. A detachable solid handle, of nominal diameter d, fits through these holes with a diametral clearance of 1%. The torque is generated by a force applied at some distance along the handle. Both components are of steel with design (tensile) stresses of 200 and 300MPa for tube and handle respectively.
    Suggest suitable dimensions for the wrench.
    Indicate the effect on the selected dimensions if the diametral clearance is changed to 5%, to facilitate handle engagement.