Stress, strength and safety problems

1. The tensile test on a steel specimen, of 12.5 mm diameter and 50 mm gauge length, gave the following results :

   	Load	(kN)	26	36	46.5	54.5	71	75	80.5	85
   	Elongation	(mm)	0.05	0.07	0.09	0.11	0.15	0.20	0.31	0.41

   Estimate the 0.2% yield strength and the elastic modulus. [ 640 MPa, 207 GPa ]
    
2. A

   Grade	A	B	C	D
   Yield (MPa)	320	360	410	450
   Relative cost	1.00	1.09	1.14	1.20

   rod of length 800 mm has to withstand a tensile force of 2 kN without its length increasing by more than 1 mm. The safety factor is laid down as 2.5 minimum.
   Steel rod is available off-the-shelf in any one of the four grades shown, and in the following diameters (mm) :     2     2.5     3     4     5     6     8     10     12     16     20     24     30
   Select a suitable grade and rod diameter for this duty.
    
3. This example introduces concepts which will be used later in the treatment of flanged joints. The 18 mm diameter eyebolt (1) is assembled through the 20 mm bore hole in the 35 mm O.D. sleeve (2), with the nut just fitting snugly. The nut is then tightened to produce an initial force in the assembly, and the load, P, finally applied. The maximum allowable stresses are 550 and 80 MPa for the bolt and sleeve respectively, and the corresponding moduli of elasticity are 207 and 50 GPa.
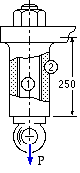
   What is the maximum load that the assembly can withstand without loss of contact, and what initial force is necessary ?
   Hint : Plot vs load the magnitudes of the forces internal to the components.   [ 136, 52 kN ]
    
4. Three 0.5 m long bars which are nominally identical and made from a 250 MPa yield steel, are connected by two pins and loaded by a force of 15 kN. The bars were designed on the assumption of equal load sharing and a safety factor of 2.5. However manufacturing inaccuracies lead to the central bar's length differing by 0.2 mm from the outers' length, thus requiring one of the pins to be forced in. Neglecting buckling, determine the actual safety factor of the assemblage if
   1. the central bar is the longest   [ 2.0 ]
   2. the central bar is the shortest   [ 1.6 ]
   
   
5. The sketch illustrates the essentials of a reinforced concrete composite member which may be loaded longitudinally either in tension, as indicated, or in compression - depending upon loads on the adjacent structure.
   The 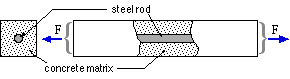member consists of a steel rod embedded in a concrete matrix. By itself, the rod would be weak in compression due to buckling; however the compressively strong concrete prevents any buckling. Conversely, concrete by itself would be weak in tension, but the steel component protects it from undue tensile effects. The two components of the composite are thus seen to complement one another.
   The member is manufactured and prestressed as follows. The steel rod is stretched by a temporary load F_o, and the concrete poured into a mould surrounding it. When the concrete has set, the mould and the load F_o are removed. Since there is no relative longitudinal displacement between steel and concrete, the steel relaxes somewhat and compresses the concrete - this prestressing occurs before external loading of the composite.
   An external tensile load, F, is finally applied to the composite member.
   Ascertain the tensile force in the concrete matrix when the composite member is loaded, in terms of the loads F_o and F, together with the longitudinal stiffness of the steel rod, k_s, and of the concrete matrix, k_c.   [   F_concrete =   ( F - F_o )/( 1 + k_s/k_c ) ]
    
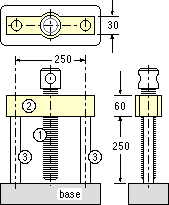6. A press consists of the central screw 1 threaded through the beam 2 which is connected to the base by the two identical tie-rods 3. All components are steel; their effective dimensions are
   1. the pitch of the central screw is 3 mm, its diameter is 20 mm and its length 250 mm;
   2. the beam is 30 mm wide, 60 mm deep, and spans 250 mm;
   3. the 250 mm long tie-rods are each 15 mm diameter.
   The screw is rotated manually until it bottoms snugly on the base. What is the stress in the tie rods when the screw is thereafter rotated by quarter of a turn? Neglect base deflections and buckling effects.   [ 209 MPa ]
    
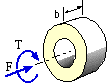7. (More difficult)   The annular disc, of radii r_i and r_o and thickness b, is supported around its outer periphery. A load is transmitted uniformly to its inner periphery by shear. Assuming that the shear in the disc at radius r is uniform, estimate the stiffness experienced by the load if it is :-
   1. an axial force, F     [ 2 π b G / ln ( r_o/r_i ) ]
   2. a torque, T     [ 4 π b G /( 1/r_i² - 1/r_o² ) ]
   
   
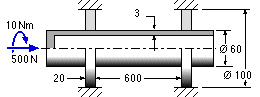8. (More difficult)   A hollow plastic tube is bonded to two identical circular rubber support collars. The allowable shear stress in the adhesive is 100 kPa. An axial force and a torque are applied to one end of the tube as shown.
   Use the results of the previous problem to deduce the bond's safety factor.
   Values of E, ν are : for plastic 2 GPa, 0.35;     for rubber 2 MPa, 0.5.     [1.05]
    
9. A plastic ball is inflated to produce membrane stresses σ_x = σ_y = 2 MPa.
   The radial thickness of the material is 0.7 mm before inflation. By how much will the thickness change after inflation if the moduli of elasticity and of rigidity are 3.5 and 1.4 GPa respectively ?     [ 0.2 mm ]
    
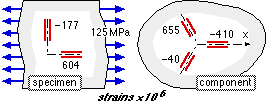10. A tensile testat 125 MPa is conducted on a specimen of a component's material. Strain gauges attached to the specimen and to the component in service indicate the strains shown.
    Find the principal stresses in the loaded component.
    [ -80, 120 MPa, -70^o ]
     
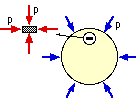11. When a solid shaft of circular cross-section is subjected to a uniform pressure, p ( due to the interference fit of a pulley boss for example ) the radial and circumferential stresses in the shaft are compressive, of magnitude p, as sketched for a typical element.
    Using the maximum shear stress failure theory, derive the design equation for a shaft cross-section of section modulus Z, loaded by such a pressure in addition to a bending moment, M, and a torque, T.
    [   n √{ (M/Z + p)² + (T/Z)² }  =   S ]
     
12. The components of the stress resultant at a particular cross-section of a 50 mm diameter ductile rod are as shown - a tensile force of 120 kN, a vertical shear force of 120 kN, a bending moment of 0.5 kNm and a torque of 1.5 kNm.
    What is the maximum equivalent stress at this cross-section?     [ 292 MPa ]
     
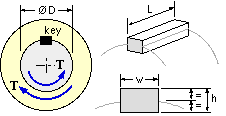13. A key's rectangular cross-section is w x h, its length is L, and it is made from a ductile material whose design tensile stress is S.
    The key is provided to transfer the load torque T between the shaft and the collar (eg. the boss of a pulley or gear). The key is fitted closely into slots machined in these components, whose common interface diameter is D, where D >> h.
    Identify the modes by which the key may fail, and derive the corresponding design inequalities which must be satisfied by the dimensions.
     
14. Determine for each of the following two-dimensional stress states (MPa) the principal stresses and the orientation of the maximum principal. Sketch the principally-oriented elements.
    1. σ_x   =       80   ;   σ_y   =   170   ;   τ_xy   =     60 c.w.       [     50,   200 MPa,   116.6^o ]
    2. σ_x   =   -220   ;   σ_y   =   -70   ;   τ_xy   =   180 c.c.w.     [ -340,   50 MPa,   56.3^o ]
    3. σ_x   =   -205   ;   σ_y   = -445   ;   τ_xy   =     35 c.w.       [ -450,  -200 MPa,  -8.1^o ]
        
15. Find the safety factors for the two-dimensional states of problem 14, if the following apply :
    1. plane stress, ductile material with yield strength of 500 MPa
       • via distortion energy theory, or       [ 2.77, 1.36, 1.28 ]
       • via maximum shear stress theory     [ 2.50, 1.28, 1.11 ]
    2. as (a), but plane strain ( ν = 0.3 )
       • via distortion energy theory, or       [ 3.59, 1.46, 1.98 ]
       • via maximum shear stress theory       [ 3.33, 1.28, 1.96 ]
    3. plane stress, brittle, with 250 and 800 MPa ultimates       [ 1.25, 1.78, 1.78 ]
    4. as (c), but plane strain ( ν = 0.2 )       [ 1.25, 1.78, 1.78 ]
        
16. Show that the distortion energy failure locus degenerates to the following alternate forms for a plane stress state :
    1.   σ_e² =   σ₁² - σ₁σ₂ + σ₂²                     where   σ₁ and σ₂ are the biaxial principals, or
    2.           =   σ_m² + 3 σ_a²                             in terms of the 'basic' components, or
    3.           =   σ_x² - σ_xσ_y + σ_y² + 3 τ_xy²   in terms of the Cartesian components.
    What ratio between shear and tensile strengths does this predict ?       [ 0.577 ]
    Plot the failure locus in ( σ₁, σ₂ ) space and superimpose the failure locus of the maximum shear stress theory for plane stress.
     
17. ( important )   The two variables y₁ and y₂ are each linearly dependent upon x in the interval 0 ≤ x ≤ L. The variable z is defined as   z   =   √( y₁² + λ² y₂² )   where λ is a constant - all parameters being real.
    Prove that any maximum of z must occur either at   x = 0   or at   x = L   - a result which will be found very useful.
     
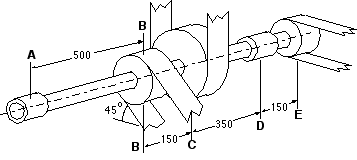18. A uniform solid shaft ABCDE is supported in bearings at A and D, and rotates at 900 rev/min (rpm).
    50 kW are delivered to the shaft through the 560 mm diameter belt pulley at C. 30 kW are extracted via the 280 mm diameter pulley at B, and 20 kW at the 210 mm diameter pulley at E. At each pulley, the two belt strands are parallel and the ratio of tensions in them is 3:1.
    Determine the minimum acceptable shaft diameter if the design stress of 100 MPa incorporates an allowance for fatigue.       [ 40 mm diameter ]
     
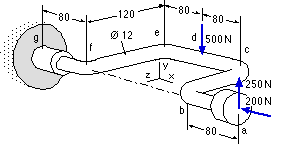19. The drill brace abcdefg   is made from a bent rod of 450 MPa yield steel, and is loaded as shown by the operator. The simple support at g also provides the torque reaction necessary for equilibrium.
    What is the factor of safety?
    [ maximum shear stress 1.21; or distortion energy 1.22 ]
     
20. The horizontal shaft ABCD is mounted in bearings at B and D as shown. A belt passes around the 250 mm diameter pulley fixed to the shaft at A, and a gear pinion of 150 mm pitch diameter is mounted on the shaft at C. Shaft diameters and axial disposition of the components are as sketched. The belt strand tensions are horizontal and in the ratio F₁/F₂ = 4, while the vertical reaction on the pinion, P, acts tangentially to the pinion's pitch circle.
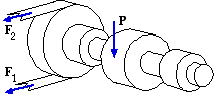
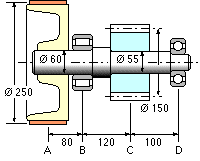
    Ascertain the shaft's safety factor when transferring 20 kW from belt to pinion at a steady 7.5 Hz, taking the yield strength of the ductile shaft material to be 500 MPa. Fatigue and stress concentration are neglected here - a large safety factor caters (?) for this neglect.
    [ maximum shear stress 14.5   or distortion energy 15.6 ]