EXAMPLE

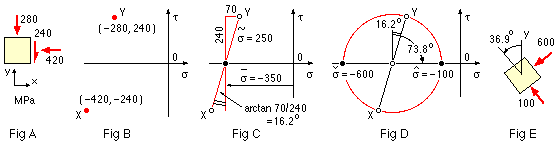
An element is stressed as in Fig A below. All stresses are in MPa.
Sketch the element oriented principally. Employing the conventions outlined above, one technique for constructing Mohr's circle is as follows :-

Fig B

By the convention, the stress state defined by Cartesian components is σ_x = -420,   σ_y = -280,   τ_xy = -240 MPa; so the points X ( σ_x, τ_xy) and Y ( σ_y, τ_yx= -τ_xy = 240 MPa) are plotted in τ-σ   space.

Fig C

Since the line X-Y is the diameter of the circle, the trigonometry of the circle requires :
                circle centre :   σ_m =   ( -280 -420)/2   = -350 MPa
                circle radius :   σ_a   = √( 70² + 240²)   = 250 MPa
                inclination of X-Y diameter to vertical = arctan( 70/240 ) = 16.2^o

Fig D

The circle is completed, noting that the two principals from ( 5) are σ_max = -100, σ_min = -600 MPa. We choose here to define the principal orientation by reckoning σ_max at 73.8^o clockwise from Y on the circle, so . . .

Fig E

. . . σ_max on the element lies at 73.8/2 = 36.9^o anticlockwise from y, which enables completion of the sketch of the principally oriented element. Alternatively the minimum might be reckoned from y, or from x, etc.

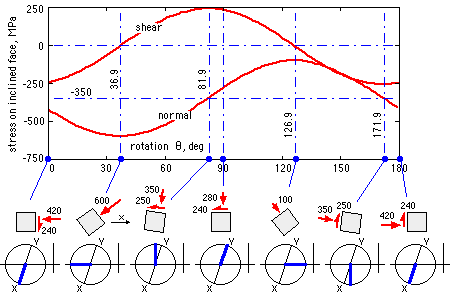
The variations of the normal and shear stresses with inclination θ, calculated from ( 4a), are plotted below together with the Mohr's circles corresponding to the inclinations of principals, of maximum shear etc. The reader should appreciate the trends indicated.

The foregoing should not be construed as being the only way for resolving a two-dimensional stress state, but it lends itself to rapid interpretation.