EXAMPLE

Given the surface strain state :   ε_x = 2 E-4 (ie. 2x10^-4),   ε_y = 10 E-4,   γ_xy = -6 E-4     determine the principal stresses, the planes in which they occur, and the stress components on the t-plane inclined at 30^o from the x-reference. Take E = 200 GPa, ν = 0.25   (ie. the material is not steel).

Analytic Approach
Transforming the given strain Cartesian components into the basic strain triad via ( 3b):-
                ε_m   =   6 E-4,       ε_a   =   5 E-4,       θ_p   =   108.4^o
Transforming from strain to stress via ( 6) :-
                σ_m   =   160 MPa,       σ_a   =   80 MPa,       ( θ_p   =   108.4^o)
So the principal stresses are :-
                σ_max   =   σ_m + σ_a   =   240 MPa   at   θ_p =   108.4^o
                σ_min   =   σ_m   - σ_a   =     80 MPa     at   θ_p ± 90^o =   18.4^o
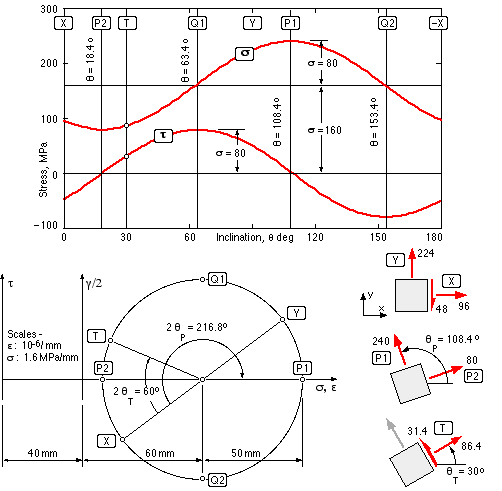
and, from ( 4a) the components at the general angle θ^o are :-
                σ   =   160 + 80 cos 2 ( 108.4- θ )^o     ;     τ   = 80 sin 2 ( 108.4- θ )^o     which are plotted below.
When θ = 30^o in the t-direction, then   σ = 86.4,     τ = 31.4 MPa.
Graphical Approach
Select a strain scale of, say $_ε = 1 E-5 per mm, in which case the points X ( 20, -30 mm ) and Y ( 100, 30 mm ) define the ends of Mohr's circle diameter.   Keep track of the units!
The strain circle is then drawn as shown, it being found that the centre lies at C_ε = 60 mm from the shear strain axis.
Converting to the stress circle via ( 7) gives $_σ = 1.6 MPa/mm, C_σ = 100 mm, which latter figure enables the shear stress axis to be located with respect to the circle centre.
Locate T at 2 x 30 = 60^o clockwise from X, hence T ( 54.0, 19.6 mm ) by measurement.
Scaling these stress components :       σ = 54.0 x 1.6 = 86 MPa ;       τ = 19.6 x 1.6 = 31 MPa       (graphics, so not more than say two sigfigs)

Finally - and this is what's important, no matter which convention or technique is used - the stresses on the oriented element should be drawn.