Answer to the double bar problem

component 1 :	n1 = ( A S / P )1	= 100 x 600 / 50 E3	= 1.2
component 2 :	n2 = ( A S / P )2	= 200 x 400 / 50 E3	= 1.6
assembly :	n   = minimum ( n1, n2)	= 1.2

On the face of it therefore the assembly (and every component thereof) is safe, since all safety factors exceed unity.

BUT . . . .

Equation ( 1b) was derived on the assumption that the stress is uniform across the cross-section, so equation ( 1b) can be applied

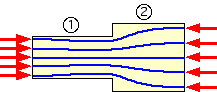
But clearly the stress cannot be uniform in component #2 at least, since the load is transmitted through the 100 sq.mm contact area at the LHE of #2 as suggested by the force pathson the sketch. Assuming that the stress is approximately uniform across the contact area, then

component 2 :	n2 = ( A S / P )2	= 100 x 400 / 50 E3	= 0.8
assembly :	n   = minimum ( n1, n2)	= 0.8

It is concluded that the assembly is NOT safe.

It is apparent that although the cross-sectional area of #2 is constant from one end to the other, the effective area through which the load is channeled is not constant. So when we refer to the safety factor of #2 as being 0.8, we're referring to the minimum safety factor which corresponds to the LHE here.