DANotes: Stress etc: Cantilever analysis example

EXAMPLE

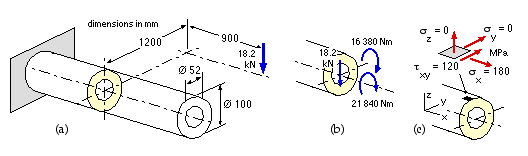
The cantilevered shaft of fig (a) is loaded only by the 18.2 kN force. Ascertain the factor of safety at the hatched cross-section if the shaft is

ductile with a yield of 350 MPa, or
brittle with tensile and compressive ultimates of 300 and 750 MPa.

Find all loads on member, resolving any static indeterminacies if necessary

The 18.2kN force is the sole load here.

Identify load building blocks and potentially critical element(s); evaluate corresponding stress components

Constructing a free body embracing the load(s) and the required cross-section, the load building blocks are found here to include bending, torsion and direct shear - fig (b). The cross-sectional element of fig (c) is identified as the most critically loaded; the stress components on it are :

bending : σ_x = My/I = 16380 x 50 x 64 / π (100⁴ -52⁴) = 180 MPa

torsion : τ_xy = Tr/J = 21840 x 50 x 32 / π (100⁴ -52⁴) = 120 MPa

The direct shear stress maximises in the centroidal x-y plane at 4V/3A = 4 x 18.2 E3 x 4 / 3 x π (100² -52²) = 4 MPa Mohrs circle for shaft example

but vanishes at the element in question; its neglect is justified. Other stresses on the element are zero.

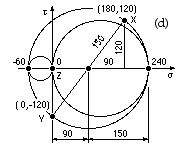
Resolve stresses to ascertain the three principals
Stresses on the x-y faces of the element are resolved by Mohr's circle fig (d) to give the principals in the x-y plane. Since there are no z-stresses, the three principals are 240, 0, -60 MPa.

Apply the relevant failure theory
Ductile :

Distortion energy ( 8) σ_e = √{ [ (240 -0)² + (0 -(-60))² + (-60 -240)² ] /2 } = 275 MPa ; n = 1.27

Max.shear stress ( 9) σ_e = 240 - (-60) = 300 MPa ; n = S_y /σ_e = 1.17
Either theory may be applied to ductiles; the maximum shear stress is clearly more conservative as it predicts a higher equivalent stress.

Brittle :

Modified Mohr ( 10) 1/n = max( 240/300 , 60/750 , 240/300 -180/750 ) = 0.8 ; n = 1.25