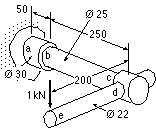
EXAMPLE
 
The torque wrench is made from a 350 MPa yield steel and loaded by 1 kN. Ascertain the safety factor based on the maximum shear stress theory.

First identify those cross-sections which appear likely to be critical - a, b and c are all subjected to a torque of 200 Nm.   c is of the same diameter as b and the bending moment there is less than that at b, so c may be neglected as being less critical than b.

cross-section	a	b	d
M   (Nm)	300	250	200
T   (Nm)	200	200	-
Me = √( M2 + T2 ) (Nm)	361	320	200
diameter, D (mm)	30	25	22
Z   (mm3) = π D3 / 32	2650	1535	1045
σe   (MPa)   =   Me / Z	136	208	191
n   =   Sy / σe	350/136	350/208	350/191
	= 2.6	= 1.7	= 1.8

Although the bending moment at b is less than at a, the diameter is also less, so it is not immediately clear which of the two sections is the more critical. At d, although there is no torque, the diameter is again different so the degree of safety is not obvious. Cross-sections a, b and d must therefore all be included in the search for the weakest link.

From this table, it is evident that cross-section b is the most critical, since its safety factor is the smallest. The shaft safety factor is   min ( 2.6, 1.7, 1.8 )   =   1.7