DANotes: Brakes: Short shoe analysis example

EXAMPLE

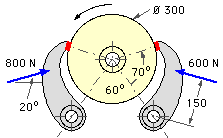
A brake consists of two identical short shoes arranged and actuated as shown. The distance between drum and hinge centres is 240 mm.
Assuming a friction coefficient of 0.5, determine :

the total braking torque on the drum, T_o
the sensitivity S of each shoe
the load R_H on each shoe hinge
the load supported by the drum shaft, R_O
the brake's practicability given that the contact area of each lining is 100 mm².


common shoe geometry - refer to short shoe sketch ( a) above
	r = 150 mm ; a = 240 mm ; e = 150 mm ; θ_m = 70^o ; so from ( 6a)
	m = 1/0.5 x 240/150 x cos 70^o = 3.007 ; and n = 1 - 240/150 x sin 70^o = 0.4528
	The "significant figures" quoted here for checking purposes are anything but - the friction coefficient accuracy is two sigfigs at the very most !
individual shoe parameters
						LEFT SHOE	RIGHT SHOE
		Shoes are external so Δ = +1				leading so δ = -1	trailing so δ = +1
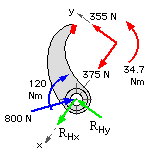
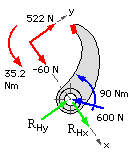
		P			(N)	800	600
		M	=	Pe	(Nm)	0.15x800 = 120	0.15x600 = 90
	(6a)	N	=	M/μr( m - δΔn)	(N)	120/0.5x0.15( 3.007+0.453) = 462	90/0.5x0.15( 3.007-0.453) = 470
	(vii)	η	=	1/( m - δΔn)		1/( 3.007+0.453) = 0.289	1/( 3.007-0.453) = 0.392
	(viii)	S	=	mη		3.007x0.289 = 0.869	3.007x0.392 = 1.177
	(5a)	F_x	=	N( Δ cosθ_m - δμ sinθ_m)	(N)	462(0.342+0.5x0.940)=375	470(0.342-0.5x0.940)= -60
	(5a)	F_y	=	N( δμ cosθ_m+ Δ sinθ_m)	(N)	462(-0.5x0.342+0.940)=355	470(0.5x0.342+0.940)=522
	(5a)	T	=	μNr or = ηM	(Nm)	0.5x462x0.15 = 34.7	0.5x470x0.15 = 35.2
		So for the brake as a whole, T_o = T_L + T_R = 34.7 + 35.2 = 69.9 Nm
		Shoe free bodies with actuation, drum contact and hinge reaction components
		R_Hx		from Σ F_x = 0	(N)	800 cos40^o -375 = 238	600 cos40^o +60 = 520
		R_Hy		from Σ F_y = 0	(N)	800 sin40^o -355 = 159	600 sin40^o -522 =-136
		R_H		by Pythagoras	(N)	286	537
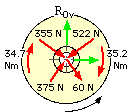
		Drum free body with reactions to above shoe-drum contacts at drum centre, and horizontal & vertical components of drum shaft support
		R_Oh		from Σ F_horiz = 0	(N)	(522-355) cos30^o - (60+375) sin30^o = -73
		R_Ov		from Σ F_vert = 0	(N)	(522+355) cos60^o + (60-375) sin60^o = 166
		R_O		by Pythagoras	(N)	181

If the brake is to be practicable then the average lining pressure p_m = N/A ( 5a) cannot exceed a value which experience has shown to be feasible - around 700 kPa for a drum brake ( see earlier R_p table). The pressure resultant N is higher for the right shoe here so the highest average lining pressure in the brake is p_m = 470/100 = 4.7 >> 0.7 MPa. The brake is clearly not practicable unless actuations and resulting braking torque are reduced to 0.7/4.7 = 15% of their values above.
Short shoe brakes just don't have enough lining area to give useful braking effects with sustainable lining pressures, however they may be applicable to one-off emergency situations.

The left shoe is counter-actuating hence requires a larger actuation than the self-actuating right shoe for approximately the same braking torque.
If the left shoe's LH coordinate system causes difficulty in comprehension, then the brake should be viewed from the rear - the left shoe in the front view becomes the right in the rear view.
We shall consider later the practical means for applying different actuation forces to the two shoes from a single control signal (eg. a car driver's stamping on the brake pedal).
The brake illustrates how the two opposed linings tend to balance one another so that the net load on drum shaft and bearings is small.