Repeat the preceding example if the mechanism is imperfect, the imperfection being characterised by an initial out- of- straightness   θ_o when the springs are free.

 
The analysis is similar to the above except that the free position is defined by   θ =   θ_o   rather than by   θ = 0.   So, as the initial deflections must increase :
          δ₁   =   2b [ ( cosθ + α sinθ ) - ( cosθ_o + α sinθ_o ) ]   ;       |θ| ≥ |θ_o|
          δ₂   =   2b [ ( cosθ - α sinθ ) - ( cosθ_o - α sinθ_o ) ]
          y - y_o   =   4b ( cosθ - cosθ_o )

For the system therefore - normalising and differentiating as before :-
        U   =   Σ k δ²/2 + P ( y - y_o )
        u   =   U/8kb²   =   ¹/₂ [ ( cosθ - cosθ_o )² + α² ( sinθ - sinθ_o )² ] + p ( cosθ - cosθ_o )
( C)       u'   =   ( cosθ_o - cosθ ) sinθ + α² ( sinθ - sinθ_o ) cosθ - p sinθ
( D)       u"   =   ( cosθ_o cosθ - cos2θ ) + α² ( sinθ_o sinθ + cos2θ ) - p cosθ

The equilibrium path, from ( 1a) and ( C) is evidently : <
( E)       p   =   cosθ_o - cosθ + α² ( 1 - sinθ_o / sinθ ) cosθ   ;       |θ| ≥ |θ_o|
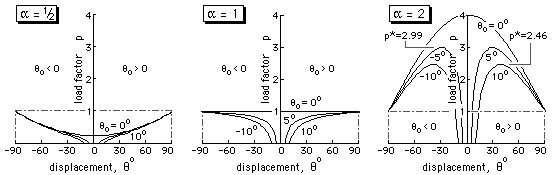
                  which is plotted below for the same three mechanism proportions as previously, for the perfect case ( θ_o = 0 ), and for positive and negative imperfections   |θ_o| = 5^o and 10^o.

Considering stability, inserting ( E) into ( D) yields :-
        u"   =   sin²θ [ 1 + α² ( sinθ_o / sin³θ - 1 ) ]

Thus, for the positive branches, stability is lost if
( F)       u"   ≤   0     ie. if       sinθ   ≥   [ α² sinθ_o / ( α² - 1) ]^1/3
                  and can only occur if   α > 1; the corresponding maximum load capacity   p* from ( F) being :
        p*   =   cosθ_o + [ ( α² - 1 )^2/3 - ( α² sinθ_o )^2/3 ]^3/2   ;       α > 1
Some values of   p* are shown above for   α = 2.