Buckling problems

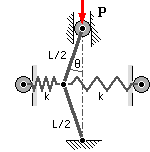
1	Show that the post-buckling paths for the perfect mechanism are :   p = 2P/kL = cosθ. Plot the   p-θ paths, and ascertain whether equilibrium is stable, neutral or unstable. If the mechanism is imperfect, with an initial out- of- straightness θo when the springs are free, show that the maximum load capacity is :   p* = [ 1 - ( sinθo )2/3 ]3/2 Plot   p* versus   θo , and also the equilibrium paths for some representative   θo .
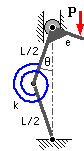2	The links of the mechanism are connected by a torsion spring of stiffness   k (Nm/rad) whose strain energy is   1 /2 kΔ2   where   Δ is the spring's angular deflection. The mechanism may embody either one of two imperfections : ( i) The load is not coaxial with the mechanism's axis, but is offset by the moment arm :   e = ε L   measured perpendicular to the upper link. ( ii) The mechanism is not straight initially, the links being inclined at   θo - in which configuration the spring is undeformed. Plot the equilibrium paths for the perfect mechanism and - for the imperfect mechanism ( i) with   θo = 0 and   ε = 0, 0.05, 0.1, 0.2, 0.5 - for the imperfect mechanism (ii) with   ε   = 0 and   θo = 0, 2.5, 5, 10, 20o Comment on the paths' shapes. Show that the mechanism is always stable.
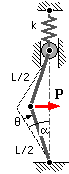3	The mechanism is inclined initially at angle   α, when the spring is free. Application of the load   P causes displacement through angle   θ. Show that the equilibrium path is       p   =   P/2kL   =   sinφ ( 1 - cosα / cosφ )     where       φ = α - θ             and plot this for   α = 22.5o   in the range   -10o ≤ θ ≤ 50o. Prove that the local maximum/minimum loads are   p* = [ 1 - ( cosα )2/3 ]3/2   and state clearly what happens when   P increases from zero.
4	A sub-sea pipeline, of nominal size   100 mm and   400 MPa yield strength, lies at   200 m. Using a safety factor of   2, select a suitable pipe wall thickness from AS 1835 to withstand buckling. A corrosion allowance of   1 mm is applicable both inside and outside the pipe. [ 6.3 mm ]
5	( a) A straight steel rod,   20 mm diameter and   200 mm long, is fixed at one end. The free end is subjected to a compressive load offset from the rod's centreline by   1 mm. What load is permissible if the maximum stress is limited to   200MPa ?   [ 37.1 kN] ( b) Repeat ( a) but with rod diameter halved.   [ 4.2 kN] ( c) Repeat ( a) but with rod length doubled.   [ 19.6 kN] ( d) Repeat ( a) but with load eccentricity doubled.   [ 28.6 kN]
6	A column is characterised by   S = 200 MPa and   σc = 150 MPa. Determine the maximum permissible compressive stress predicted by each of the three imperfect column models - equations ( h) - for   η = 0.1 and for   η = 1.0. Comment on the significance of the form and magnitude of the imperfections demonstrated by these values.   [ 121.7, 124.6, 125.0;   66.7, 69.3, 69.7 MPa]
7	A   1 m long pin-ended column is made from a   250 MPa yield,   10 mm thick, 80x80 mm equal angle section. Assuming an equivalent eccentricity of   L/1000, determine the maximum allowable load with a safety factor of   2.   [ 153 kN] Repeat this if the column is nominally perfect with   ση = 60 MPa.   [ 156 kN]
8	( a) The critical Euler stress of a column is   σc and the eccentricity ratio is   η. It is made from a brittle material with compressive and tensile strengths   Sc and St respectively. Prove the following algorithm from which the direct compressive stress   σd may be calculated :       If         1/( Sc - St ) - η/( Sc + St )   <   1/( 2 σc )       then     σ2d + σd [ St - ( 1 - η ) σc ] - St σc   =   0       else       σ2d - σd [ Sc + ( 1 + η ) σc ] + Sc σc   =   0       Hint : Apply equation ( g) to the convex side where bending stresses are tensile ( b) A   400 mm long end-fixed column is made from a cast iron whose compressive strength is   765 MPa. The cross-section is square,   20x20 mm, and due to fears of casting inaccuracies, an eccentricity ratio of   1 is assumed for estimating purposes. What maximum load can the column withstand on this basis ?   [ 85kN]
9	Trial-and-error methods must be employed when applying equation ( 3) to the design of ductile columns. Input constraints necessary for the design process include the column equivalent length,   L, the actual load,   F, and desired safety factor,   n. A range of sections is chosen - of one material whose known properties include the elastic modulus,   E, and yield strength, S.   A value for the imperfection stress,   ση , also results from this choice. The trial-and-error process commences by selecting one particular section from the range, of area   A, and minimum second area moment   I. Equation ( 3) enables calculation of the corresponding safety factor. This process is repeated until the safety factor is just larger than the desired value. ( a)   Prepare a calculation sequence using consistent units to assist in the above task. ( b)   A 2.4 m long, nominally straight pin-ended column has to support a   300 kN load with a safety factor of   2. A range of   250 MPa yield steel sections is available for which the imperfection stress,   ση = 60 MPa. What size of section should be used if the sections are :- geometrically similar, with I/A2 = 0.15 ?   [ 4200 mm2] tubes with an outside diameter-to-thickness ratio of 15 ?   [ 120 mm diameter] standard channels whose properties are listed in the references ?   [ 229x89 mm]
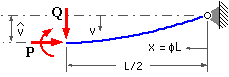10	The sketch illustrates the right half of an ideal pin-ended column which is subjected to a transverse load   Q at its centre, in addition to the compressive load   P. Using the nomenclature of the preceding notes, show that the elastic curve is : v/L   =   ( Q/P ) [ sin( π√ψ.φ )/( π√ψ .cos( π/2 √ψ )) - φ ] Hence derive the design equation for this loading, analogous to equation ( 2) above :       σd   =   S - σQ.tan( π/2 √ψ )/( π/2 √ψ )             where   σd = nF/A   and   σQ = 1/2Q L ymax /I   is the maximum bending stress due to the transverse load   Q acting alone. Plot   σd versus slenderness ratio for some representative values of the parameter   σQ - say 0, 5, 20, 50, 100, 200 MPa - and compare the behaviour with that of imperfect columns with eccentricity ratio as the parameter.