Complete the last example and find the failure load, given the previous results   σ_E   =   401,     σ_P   =   840 MPa.

Inserting these two values into the interaction models and solving for the failure load gives :-
CEGB R6 model - from ( 3)     σ_F   =   382 MPa
'circular' model   - from ( 4)     σ_F   =   362 MPa     - conservative as noted.

Using the same 20x2 mm long strip, apply the R6 approach to find the critical crack length for a 250 MPa load.

This is the reverse problem to the above - a closed form solution is impossible, so a graphical or trial- and- error approach must be adopted - thus :-

Trial normalised crack size α	0.1	0.2	0.3	0.4	0.5	0.6	0.63	0.7
σE = KIc /( Y√(παw))   corresponding to α	887	615	486	401	335	279	263	227
σP = Sy ( 1 -α )   corresponding to α	1260	1120	980	840	700	560	518	420
σF from ( 3) corresponding to σE and σP	800	578	462	382	320	265	250	214

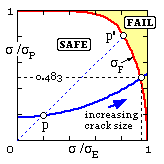The stress ratios computed from the table are plotted to illustrate the fatigue locus as crack size increases.
The safety factor at any point,   p, on the locus is the ratio   0p'/0p.
Failure occurs when   σ_F/σ_P = 250/518 = 0.483 here, corresponding to α= 0.63 - the critical crack size is therefore 0.63x20 = 12.6 mm

Repeating this for comparison purposes using the more conservative 'circular' model.
Despite this model's equation being simpler than the R6 equation, a closed form solution is impossible and the above table must be repeated using ( 4) rather than ( 3).
Thus at   α = 0.6   from the above table using ( 4)   σ_F   =   1/√( 1/279² + 1/560² )   =   250 MPa

The critical crack size predicted by the 'circular' interaction model is therefore 0.60x20 = 12 mm - not significantly different from the R6 conclusion.