First estimate the minimum dimension necessary for plastic effects to be ignored.
From ( 2a)   b_o   =   2.5 ( 50/1400 )²   =   3.2 mm. Although this is less than the ligament length of 6 mm, it exceeds the thickness of 2 mm, so plastic effects are not necessarily negligible and we would expect both failure mechanisms - elastic fracture and plastic collapse - to interact.
Letting the normalised crack length be   α = a/w = 4/10 = 0.4, the critical load arising from each of the mechanisms acting independently is as follows :

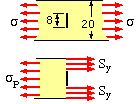
Plastic Collapse     Let   σP be the critical load if plastic effects dominate, then from the free body above :
	σP   =   Sy ( 1 - α )   =   1400 x 0.6   =   840 MPa
Elastic Fracture     Let   σE be the critical load if elastic effects dominate ( ie. plane strain ), then :
	KIc   =   σE Y √( πa )       where, for case ( a)     Y   =   √( sec α π/2 )   =   1.11     and so
	σE   =   50/( 1.11 √( 0.004 π ) )   =   401 MPa     don't forget the units !

It would appear that elastic fracture plays the major role and that the critical load is somewhat less than 401 MPa - though not much less because 840 >> 401. But we cannot be more definite at this stage.