Squirrel cage motor problems

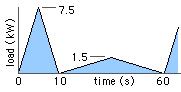
1. A load fluctuates cyclically as shown. Determine the mean effective load and select a motor suitable to drive it, using an exponent of (a) 2, (b) 5 in the equivalent load equation.
   [ 100 LB, 112 M]
    
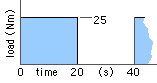2. Select a motor to drive a load whose inertia is 0.2 kg.m² and which varies periodically as shown.
   [ 132 S]
    
3. When driven at 1450 rpm a fan delivers 10 m³/s against a head of 120 mm water gauge. The fan's efficiency is 78%, its rotor's inertia is 3.5 kg.m², and bearing friction accounts for a constant torque of 10 Nm.
   Select a motor to drive the fan and estimate the running speed and acceleration time. Check your results with the program 'Motors'.
   [ 180M, 1472 rpm, 2.7s ]
    
4. The inertia of a dewatering drum is 400 kg.m². Friction and windage are estimated to contribute equally to the drum's power requirement of 6 kW at its nominal operating speed of 250 rpm.
   Select a motor to drive the drum through a 5.75 : 1 reduction gearbox.
   [ 160 M ]
    
5. This problem concerns the effect of system inertia,   J, in reducing the torque fluctuations experienced by a motor which drives a cyclically varying load consisting of a sinusoid of period   t_o and amplitude   T_a superimposed on a mean torque of   T_m ( where T_a ≤ T_m ). That is, the load is of the form   T_m + T_a sin 2πt/t_o.
   Assuming the motor torque -speed characteristic at the mean torque,   T_m , to be approximately linear with negative slope of   'k' ( Nms/rad ), show that the amplitude of the motor torque excursions,   T_v , about the mean, is given by :
   T_v / T_a = [ 1 + ( 2π J/ k t_o )² ]^-1/2     ie < 1.
    
6. The duty cycle of an automatic punch may be represented by a sinusoid of period 5s, between the limits of 10 and 210 Nm. It is proposed to drive the punch by a 180M motor in conjunction with a flywheel, such that the system inertia is 20 kg.m². The punch will not be loaded until the motor has run up to speed.
   Discuss the feasibility of the proposal using the results of the previous problem in conjunction with an exponent of 2 in the equivalent load equation ( 3).
    
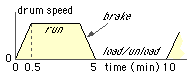7. Select a motor to drive a fairground machine which consists of a 5 m diameter rotating drum. The drum loaded with people accelerates for 30s; it then runs at constant speed before slowing to a stop for passenger exchange prior to the next cycle. The motor runs continuously, even while the drum is stationary.
   The motor drives the drum through an hydraulic coupling and a 70:1 speed reducer whose efficiency is 75%. The loaded drum's inertia is 10 t.m². Its power consumption due to friction is negligible, ie. it needs appreciable power only for acceleration.
   [ 90 S ]
    
8. A family of geometrically similar hydraulic couplings includes the sizes :-
   180, 205, 235, 265, 290, 325, 370, 415, 450, 510, 585, 660, 735, 815, 915, 1040 mm
   for which the torque characteristic at small slips is given by :
   T ( kNm ) = 0.9 d⁵ n² s ( 1.5 - s )     where d is the size (m) and n (rev/s) the impeller speed.
   Select a coupling for use with a 132M motor in the drum drive of Problem 4 and determine the speed of the drum. Note that the coupling is interposed between motor and gearbox.
   [ 265 mm, 242 rpm ]
    
9. A flexible shaft coupling can operate satisfactorily only when the shaft misalignment is less than a certain limiting value. This problem concerns the measurement and subsequent minimisation of misalignment prior to coupling assembly.
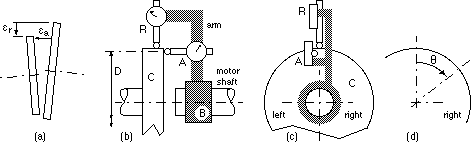
   Misalignment may be measured by the arrangement of Fig (b). An arm is mounted on the motor shaft eg. by means of the boss B. Two dial gauges are rigidly attached to the arm, their styli bear upon the coupling half, C :
       - gauge R measures radial runout   ε_r resulting from shaft radial misalignment, Fig (a), and
       - gauge A measures axial runout   ε_a resulting from shaft angular misalignment.
   Radial and angular misalignments are independent of one another, as are   ε_r and ε_a .
   Gauge readings are recorded against rotation angle   θ, Fig (d), as the shafts are rotated together slowly by hand. Neglecting any inconsequential mean value, the variation of each (small) runout is sinusoidal :     ε = ε_o cos ( θ - θ_o )     the amplitude   ε_o and phase   θ_o of which enable correction of the misalignment, radial or angular as the case may be, by means of adjustments to the motor mounting position.

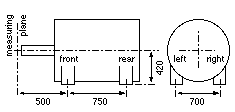
   For a particular motor the locations of the shaft and measuring plane in relation to the four mounting bolt positions are sketched.
   The following readings [ 1 gauge division = 0.01 mm ] are obtained as above, gauge A readings being taken at the diameter   D = 400 mm, Fig (b) :

   angle from vertical, θ (deg)	0	45	90	135	180	225	270	315
   reading (divisions) of radial gauge R	61	65	43	7	-20	-22	-3	31
   reading (divisions) of axial gauge A	37	26	29	46	69	80	79	61

   
   What displacements of the motor mounts are necessary to minimise misalignment ?
   [ front 0.77 up, 0.85 right;   rear 1.33 up, 1.77 right (mm) ]