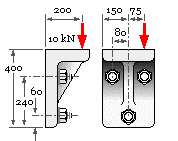
Example

Free Body # 1 - the simplest FB, envisaging the bracket as a particle in side view.
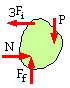Contact with the vertical support plane is represented by the normal and friction components, N and F_f respectively. If breakaway is imminent and the bracket is equilibrated solely by friction and bolt tension, then :
P_breakaway = F_f = μN = μ 3 F_i where F_i is the initial tightening load.
Assuming a typical friction coefficient of 0.35 and an initial tightening force of 90% proof then
P_breakaway = 50 kN = 0.35 x 3 ( 0.9 x A_s x 650 ) ;     A_s = 81 mm²   ie.   M12 x 1.75 bolts are called for.

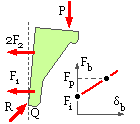
Free Body # 2 - side view.
A more complex FBD of the side view recognises the non-particle nature of the bracket, which is assumed to be rigid and to rotate about the point Q where the support plane's concentrated reaction is R. The bolts deform ( δ_b ) beyond the initial state now that this rotational separation has occurred, so the forces in each of the two upper bolts F₂ will be greater than the load in the lower bolt F₁. Since the small opening angle = δ₁/60 = δ₂/240 it follows that δ₂ = 4δ₁ so that from the bolt characteristic ( F₂ -F_i ) = 4( F₁ -F_i).
For rotational equilibrium about the point Q :
60F₁ + 240 x 2F₂ = 200 x P   which, using the above, gives   99F₂ + 9F_i = 40P = 2000 kN

Assuming that the maximum bolt force F₂ equals the proof load F_p at the design load P, and that the initial tightening load is 90% of proof, it follows that ( 99 + 9 x 0.9) A_s x 360 = 2 E6 N ;     A_s = 52 mm²
So this model is by itself less critical than that of FB#1 in which total support is by friction - but this is not surprising because FB#2 says nothing about vertical equilibrium, assuming it to be achieved by the friction component of R at Q. Furthermore, the eccentricity of the load in the front view has not been addressed.

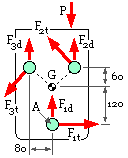
Free Body # 3 - front view
In this model the bracket is again presumed to be rigid, and equilibrium is taken to be achieved by shear of the bolt shanks, in a manner similar to sketch ( c) above. The centroid of the three equal shear areas A is located at G as shown. Since G does not lie on the line of action of the external load, a rotational tendency ( torsion ) exists.
Analysis is similar to the traditional analysis of fillet welds in that force equilibrium is achieved by uniform direct shear, while torsional equilibrium arises from secondary shear whose sense is perpendicular to the radius from the centroid to the location of the secondary shear, and which is proportional to that radius, given by the torsion equation
F_t = A τ = A ( T r/J ) = A Tr/Σ A r²     and since all A's are the same here   F_t = Tr/Σ r².
So the torsional shear forces are
F_t1 = ( P x 75) x 120/( 120² + 2 ( 60² + 80² ))   [ note units check ] = 90 P/344
F_t2 = F_t3 = F_t1 x 100/120 = 75 P/344.
The three equal direct shear forces equilibrate the force P, ie. F_1d = F_2d = F_3d = P/3.
The bolt 2 is most critical since primary and secondary most nearly coincide in it. Combining these vectorially, the total shear force on the critical shank is   F₂ = 0.5243 P = 26.2 kN. Assuming the distortion energy failure theory, the proof strength in shear is 650/√3 = 375 MPa, so the required shank diameter is √(4 x 26200/ 375 π) = 9.4 mm ie. M10 is adequate. But of course this neglects friction and the prying action recognised by FB #2.

Free Bodies # 2 & 3
Combining the above, a conservative design approach assumes the support plane to be completely smooth, so that vertical equilibrium is achieved by shank shear, and R at Q is normal to the support plane.
From FB #2 assuming F_i ≈ F₂ :   tensile F₂ = 2000/( 99+9) = 18.5 kN and so   σ = 18.5 /A
From FB #3 :                                       shear   F₂ = 26.2 kN and so   τ = 26.2/A
Applying Mohr's circle and the maximum shear stress theory to this state ( σ,τ), the equivalent normal stress is   σ_e = 2√( ( σ/2)² +τ² ) = 55.6/A from above, and = S_p at failure. So shank size = √( 4 x 55.6E3 / 650 π ) = 10.4 mm. So use M12x1.75 bolts.
It is fortuitous that the solution from this model is the same as that from FB #1.

Clearly the assumptions here are rather unrealistic - a completely rigid bracket, accurately located bolt holes ensuring theoretical sharing of shear, and so on. Anyhow, we would probably use larger bolts which 'looked right'!