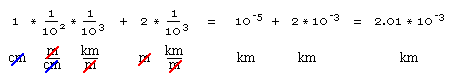
Unit
All meaningful measurements in engineering science consist of at least two parts - a magnitude and a unit. Thus the measurement 3 metres consists of the magnitude or number, 3, and the unit, in this case the metre.
Entity
A unit is measure of a certain physical 'entity', for example the centimetre unit is a measure of the entity length, the kilometre/hour a unit of the entity speed, and so on.
Entity Inter-Relationship - Dimensions
For any particular physical system under review, it is convenient to class the entities which occur in it as either fundamental or derived. The fundamental entities are those which are selected - purely on convenience grounds - as basic buiding blocks of the system. The derived entities are then expressible as combinations of the fundamentals raised to certain powers - we say that the derived entities 'have certain dimensions'in the fundamentals.
Suppose for example a geometric system was being examined - a system comprising the entities length ( denoted by [L] ), area [A], volume [V] and angle [φ]. Suppose also that length is chosen to be the fundamental entity, in which case area may be conceived as a length multiplied by a length - this is written dimensionally as [A] = [L]*[L] = [L2] - that is the derived entity area has the dimensions of length squared. Similarly [V] = [A]*[L] = [L3] and [φ] = [L]/[L] = [L0] = [ ] since an angle may be thought of as the arc length of a circular sector divided by its radius. Entities in which the powers of the fundamentals are zero are termed 'dimensionless', written [ ].
Alternatively, if volume had been selected as fundamental, then [L] = [V1/3], [A] = [V2/3] while [φ] remains dimensionless in terms of any fundamental.
Homogeneity of Equations
The equation : 1 kilometre + 2 litres = 3 seconds is obviously meaningless, and is so because the terms are of different entities. An equation must be entity homogeneous - ie. the terms of the equation must all be of the same entity - before the arithmetic 1 + 2 = ? can be carried out.
Entity homogeneity is not always so obvious as in the above example. Suppose we set out to calculate the area 'A' of the Earth's surface which is visible from an aeroplane flying at height 'h' above the surface, the Earth being assumed spherical of radius 'r'. Suppose we came up with the expression : A = 2π h r3 / (r+h). Choosing length [L] as the fundamental entity, then the dimensions of the RHS of this equation are : [L0]*[L1]*[L3]/([L]+[L]) = [L4]/[L1] = [L3] since 2π may be regarded either as a pure number or as an angle, both of which are dimensionless.
The LHS of the equation, being an area, has the dimensions [L2], so the dimensions of the two sides of the equation are different - the equation is not dimensionally homogeneous and must therefore be wrong - we can spot the error immediately. The necessity for entity homogeneity leads to a powerful technique known as Dimensional Analysis for actually setting up the form of the equations governing any physical system, as opposed to the mere checking above. We shall not examine the technique further here.
Consider now the equation : 1 centimetre + 2 metres = 3 kilometres. This too is obviously incorrect even although it is homogeneous in the entity length. It is wrong because the units of the various additive terms are not identical - the equation is not unit homogeneous and so 1 + 2 ≠ 3. The process of homogenising this simple equation will be second nature to the reader, however the underlying principles of homogenisation still apply, and must be spelt out in detail, when dealing with more complicated functions. The technique is outlined below.
Conversion Factors
Conversion factors are dimensionless numbers which inter-relate, or convert, different units of the same entity. Thus '100 centimetres/metre' and '60 second/minute' are familiar conversion factors - their dimensions are respectively [L]/[L] = [ ] and [T]/[T] = [ ] where 'T' is the entity time.
Considering the above equation : 1 cm + 2 m = ? again, the homogenising procedure is :
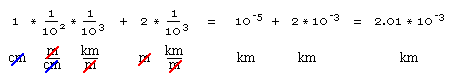 |
Introduction to Unit Systems
Although the Systeme International d'Unites (SI) is now firmly established as the standard system of units in this country, the US system - which is similar to the old Imperial System - is still very common in the mineral and resource processing fields, and looks likely to remain so for some time. This, and the necessity to interpret overseas texts, means that engineers must be fluent in systems other than the SI. We shall examine the SI and the Imperial below, with a view to illustrating the techniques of converting from any one system to any other.
Three fundamental entities only are a necessary foundation for Mechanics (though Thermodynamics and Electricity each requires an additional fundamental). Those usually selected - on the basis of simplicity - are length [L], mass [M] and time [T], and their units are defined arbitrarily. The units of the derived entities are then based on these fundamental units.
Newton's Second Law
This law, which states that : force = mass * acceleration is the foundation of Mechanics, and must be homogeneous in both entities and units. Acceleration is 'time rate of change of velocity', that is a velocity increment divided by a time increment - velocity itself being displacement per unit time. So [acceleration] = ( [L]/[T] )/[T] = [LT-2 ] where L and T are fundamental. For entity homogeneity therefore, Newton's Law requires that the dimensions of the derived entity force, F, are given by : [F] = [M]*[LT-2 ] = [MLT-2 ].
For unit homogeneity on the other hand : units of force = units of mass * units of length / (units of time)2 and to ensure this the equation is written : force = mass * acceleration / gc where gc is a dimensionless conversion factor inserted to preserve unit homogeneity in whatever system is being used - that is each system is characterised by its own unique gc.
It will be seen below that in some systems the magnitude of gc equals the magnitude of standard gravitational acceleration - this results from the manner in which the unit of the derived entity force is defined in the system and is NOT due to any supposed direct dependence of gc on gravity - gc has got nothing directly to do with gravity - it is simply a conversion factor.
The Systeme International
In this system the standard units of the fundamental entities are defined as follows :
| mass | - | kilogram | (kg) | : | the mass of an arbitrary lump of platinum | |
| length | - | metre | (m) | : | an arbitrary number of wavelengths of atomic krypton radiation (nominally an even fraction of the Earth's equatorial circumference) | |
| time | - | second | (s) | : | an arbitrary fraction of the year 1900 |
The weight, W, of a mass of 5 kg for example, is the force exerted by the Earth on the mass, accelerating the mass if not equilibrated at the acceleration of gravity (for which the standard value is 9.81 m/s2 ). So:
W = ma/gc = 5 {kg} * 9.81 {m/s2 }/ 1 {kg.m/N.s2 } = 49 N
The reader is advised to follow through the cancelling of units here, in a manner similar to the '1+2=?' equation above. Systems like the SI in which the magnitude of gc is unity are called 'absolute' systems.
The Imperial System
In the Imperial System the unit of mass, the 'pound' (lb), and the unit of length, the 'foot' (ft), are currently defined in terms of SI units - conversion factors of 2.205 lb/kg and 0.3048 m/ft apply - while the unit of time is identical to the SI second.
The unit of force, the 'pound force' ( lbf ), is defined as the weight of a pound mass under standard gravity conditions when the acceleration is 32.174 ft/s2 . The value of gc for the Imperial system is found in a manner identical to the above :
gc = ma/F = 1{lb} * 32.174 {ft/s2 }/1 {lbf} = 32.174 lb.ft/lbf.s2
The weight of a 5 lb mass under standard gravity conditions is therefore :
W = ma/gc = 5 {lb} * 32.174 {ft/s2 }/32.174 {lb.ft/lbf.s2 } = 5 lbf
Again, the reader should confirm manipulation of the units. Systems like the Imperial in which a mass's weight is equal numerically to the mass itself are called 'gravitational systems'. US notation differs from the Imperial in using the abbreviations 'lbm' for pound mass, and 'lb' for pound force.
Suppose it is required to find the weight of a body, WM, at a point on the Moon where the gravitational acceleration is 5.2 ft/s2 , the body weighing 3 lbf under standard Earth gravity conditions. From the above, we see immediately that the mass of the body is 3 lb, so, using the last equation
WM = ma/gc = 3{lb} * 5.2{ft/s2 }/32.174 {lb.ft/lbf.s2 } = 0.48 lbf
Conversion of force from one system to another is usually most easily carried out by invoking the gc factors of the two systems. Thus to find the Imperial equivalent of 10 N, we have :
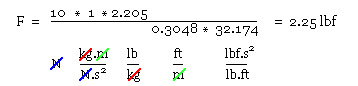
|
Energy
All forms of energy - be they mechanical, thermal, electrical, nuclear etc. - are equivalent, that is they have the same dimensions. The two forms of most immediate interest to us are thermal energy or 'heat', Q, and mechanical energy or 'work', W (whose symbol should not be confused with that of weight). Their equivalence is expressed in the First Law of Thermodynamics : W = Q (briefly, this will be formulated more rigorously in Thermodynamics).
Work, a derived entity, is conceived as that which is done when a force moves its point of application, and is the product of the force and the distance moved in the direction of the force, so :
[energy] = [force] * [distance] = [MLT-2 ] * [L] = [ML2 T-2 ]
The unit of work, energy and quantity of heat in the SI is the 'Joule' { J } which is defined as the work done when a force of 1 N moves its point of application through a distance of 1 m - ie. a conversion factor of 1 J/Nm applies.
In the Imperial system, different units are used for thermal and mechanical energies, so a conversion factor 'J' is necessary in the First Law statement, thus : W = JQ.
J is sometimes referred to as 'the mechanical equivalent of heat', however it's just another conversion factor - analogous to Newton's gc but for the entity energy/work/heat. The Imperial unit of work is the foot-pound force { ft.lbf }, and the unit of heat is the British Thermal Unit { BTU }. Using these units, J has the value of 778 ft.lbf/BTU (approx). So, from the First Law, the amount of work which is equivalent to 10 BTU of heat is :
W = 778 { ft.lbf/BTU } * 10 { BTU } = 7780 ft.lbf
When inserting values into algebraic equations, the reader is strongly advised to adopt the technique used above, in which :