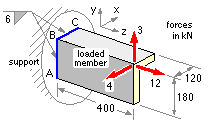
Geometric properties of the run :-
      b = 120     d = 180     L = 300 mm
The centroid is located via the above table of run properties.
B lies at   ( -24, 54, 0 ) mm in the centroidal system, and
      I_xx   =   d³ (4b+d)/12L   =   1.0692 E6 mm³     - note the units
      I_yy   =   b³ (4d+b)/12L   =   0.4032 E6 mm³     - hence   J_zz   =   I_xx + I_yy   =   1.4724 E6 mm³
      I_xy   =   b² d² /4L   =   0.3888 E6 mm³ - but this is not used in the traditional approach

Centroidal loading :-
The known loads on the loaded member are transferred to the run centroid, with introduction of the requisite moments. It is clear by inspection here that the resultant centroidal force is   F   =   [ -4   3   12 ]' kN using the given Cartesian system. The resultant moment may be found either from three orthogonal views or by vector algebra.
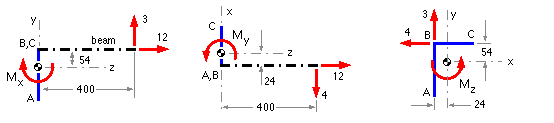
The three views are shown here, one moment component being ascertained by the RH rule from each view :

view direction	positive x	negative y	negative z
diagram showing loads' moment about centroid
centroidal load, kN	Fy = 3 ;     Fz = 12	Fx = -4 ;     Fz = 12	Fx = -4 ;     Fy = 3
moment of load about centroid (RH Rule), Nm	Mx = 12*54 -3*400 = -552	My = 12*24 -4*400 = -1312	Mz = 4*54 -3*24 = +144

In summary, the centroidal loading is :-     F   =   [ -4   3   12 ]' kN ;     M   =   [ -552   -1312   144 ]' Nm
Alternatively the loads' moment about the centroid may be obtained from vector algebra :
      M   =   r x F   =   [ -24   54   400 ]' x [ -4   3   12 ]' kN.mm   =   [ -552   -1312   144 ]' Nm

Intensity components at line segment end-points for equilibrium :-

Primary :         q_p   =   -F/L   =   [ 4   -3   -12 ]' x 10³ /300   =   [ 13.3   -10   -40 ]' N/mm

view direction	positive x	negative y	negative z
Secondary : diagram showing sense of secondary intensity to equilibrate centroidal moment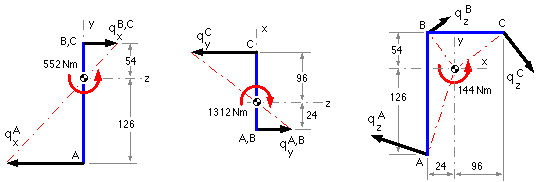
	out-of-plane bending	out-of-plane bending	in-plane torsion
formula - check units	qx = Mx y / Ixx	qy = My x / Iyy	qz = Mz r / Jzz
intensity component at A (magnitude from formula; sign by inspection), N/mm	qxA= -552*126/1.0692= -65.1	qyA= 1312*24/0.4032= +78.1	qzxA= -144*126/1.4724= -12.3   qzyA= 144*24/1.4724= +2.4
. . . and at B, N/mm	qxB = +27.9	qyB = +78.1	qzxB = +5.3   qzyB = +2.4
. . . and at C, N/mm	qxC = +27.9	qyC = -312.4	qzxC = +5.3   qzyC= -9.4

The double subscript notation has the first subscript representing the axis about which the secondary intensity acts, a second subscript denotes the sense of a component of secondary intensity.
Thus for the in-plane intensity at the point A :
      r_A   =   √( 24² + 126² )   =   128.3 mm
      q_z   =   M_z r / J_zz   =   144 E3 ^_* 128.3 /1.4724 E6   =   12.5 N/mm
      Resolving this into x, y components by similar force and dimensional triangles with signs by inspection :
      q_zx   = -12.5 ^_* 126/128.3 = -12.3 N/mm
      q_zy   =   12.5 ^_* 24/128.3   =   2.4 N/mm

Resultants :-

The resultant intensity at each point is the sum of all components, primary and secondary :-
      q_A   =   [ ( 13.3 -12.3 ) (-10.0 +2.4 ) ( -40.0  -65.1 +78.1 )]'   =  [   1.0   -7.6   -27.0 ]' N/mm
      q_B   =   [ ( 13.3  +5.3 ) (-10.0 +2.4 ) ( -40.0 +27.9 +78.1 )]'   =  [ 18.6   -7.6   66.0 ]' N/mm
      q_C   =   [ ( 13.3  +5.3 ) (-10.0  -9.4 ) ( -40.0 +27.9-312.4)]'   =  [ 18.6   -19.4   -324.5 ]' N/mm

The problem is not pursued any further, to ascertain safety for example, because the numerical values are WRONG - the traditional approach does not cater for asymmetric bending which occurred in this example run. Although   I_xy was evaluated, it was not used.