
Code_Aster
®
Version
7.4
Titrate:
Law of behavior (in 2D) for the steel-concrete connection: JOINT_BA
Date:
09/09/05
Author (S):
S. MICHEL-PONNELLE, NR. DOMINGUEZ
Key
:
R7.01.21-A
Page
:
1/26
Manual of Reference
R7.01 booklet: Modelings for the Civil Engineering and the géomatériaux ones
HT-66/05/002/A
Organization (S):
EDF-R & D/AMA
Manual of Reference
R7.01 booklet: Modelings for the Civil Engineering and the géomatériaux ones
Document: R7.01.21
Law of behavior (in 2D) for the connection steel
concrete: JOINT_BA
Summary:
The law of behavior JOINT_BA describes the phenomenon of degradation and rupture of the connection between
bars of steel and concrete, in the reinforced concrete structures. This documentation presents the theoretical writing
in the thermodynamic framework and the numerical integration of the law, as well as the parameters which manage it
model.
For his use, one will be pressed on the finite elements of gasket type (see Doc. [R3.06.09]) already existing in
the code.

Code_Aster
®
Version
7.4
Titrate:
Law of behavior (in 2D) for the steel-concrete connection: JOINT_BA
Date:
09/09/05
Author (S):
S. MICHEL-PONNELLE, NR. DOMINGUEZ
Key
:
R7.01.21-A
Page
:
2/26
Manual of Reference
R7.01 booklet: Modelings for the Civil Engineering and the géomatériaux ones
HT-66/05/002/A
Count
matters
5.2.2
The parameter of damage A
1DT
for the passage of the small deformations with

Code_Aster
®
Version
7.4
Titrate:
Law of behavior (in 2D) for the steel-concrete connection: JOINT_BA
Date:
09/09/05
Author (S):
S. MICHEL-PONNELLE, NR. DOMINGUEZ
Key
:
R7.01.21-A
Page
:
3/26
Manual of Reference
R7.01 booklet: Modelings for the Civil Engineering and the géomatériaux ones
HT-66/05/002/A
1 Introduction
The law of behavior JOINT_BA describes the phenomenon of degradation and rupture of the connection
existing enters the steel bars (smooth or ribbed) and the concrete surrounding it. Key point for
the purpose of structural design out of reinforced concrete, the modeling of the steel-concrete connection is
representation as well as simplification of this phenomenon complexes interaction between the two
materials which develops in the interface and which undergoes an increasing degradation when one
exceed certain thresholds of resistance, specific for each material. The structural models which
do not take into account the linkage effects, are generally unable to predict
localization of the fissures as well as the networks created. In addition, the degradation of the rigidity of
connection increases the period of vibration, reduced the capacity of dissipation of energy and conduit to one
significant redistribution of the internal forces (according to Bertero, 1979, cf [bib2]).
The law of behavior JOINT_BA is described within the framework of the thermodynamics of the processes
irreversible: the writing and L `use of a “conventional” material model coupling cracking and
friction makes it possible to integrate in a robust way of the fine mechanisms nonlinear concomitant into
particular description of the kinematics of slip. This last point allows us not
to resort to conventional modelings of the type “contact” very often used in this context in spite of
many sources of numerical instabilities. Thus, in monotonous loading the taking into account
coupling normal effort shearing makes it possible to treat cases of strong multiaxial pressures; in
cyclic, the behavior hysteretic and corresponding dissipations are expressed thanks to
coupling between the state of damage and kinematic work hardening. Use of an implicit scheme
allows to obtain a robust implementation.
The paragraph [§2] described in short form the phenomenon of the connection steel concrete. The paragraph [§3]
present the thermodynamic writing of the law of behavior, while the paragraph [§4] precise
the numerical stage of integration of the law. The parameters which manage the model and which could be
obtained starting from the properties of implied materials, are described in the paragraph [§5].
2
Short description of the steel-concrete connection
Conceptually, the phenomenon of connection corresponds to the physical interaction of two materials
different, which occurs on an area of interface by allowing the transfer and the continuity of the efforts
and of the stresses between the two bodies in contact. In the case of reinforced concrete structures, it
phenomenon is also known as the “rigidity of voltage” which develops around an element of
reinforcement, partially or completely embedded in a volume of concrete. Forces of traction which
appear inside the reinforcement are transformed into shear stresses on
surface, and are transmitted directly to the concrete in contact which will balance them finally, and vice
poured. The response of the unit will depend on the capacity of the concrete to become deformed as much as steel,
since steel will tend to slip inside the concrete surrounding it. The phenomenon of connection
corresponds to this capacity of the concrete to become deformed and to degrade themselves locally by creating a species
of layer, or wraps, around the reinforcement, of which the properties kinematics and material
differ from those of the remainder from the concrete or reinforcement employed.
The phenomenon can be broken up into three well defined mechanisms:
·
a chemical adherence of origin,
·
a mechanism of friction between two rough surfaces (steel-concrete or concrete-concrete),
·
a mechanical action created by the presence of the ribs of the steel bar on the concrete
bordering.
According to this decomposition, one can clearly deduce that for a smooth bar, the mechanism
dominating is friction between two materials, while for a bar ribbed (in
French usually called “braces ha: High Adherence”), the mechanism dominating is
the mechanical interaction between surfaces. When the reinforcement is consisted the wiring with
steel wire ropes, it is possible to control or combine the various mechanisms since they are
function directly of the surface of the cables.
Code_Aster
®
Version
7.4
Titrate:
Law of behavior (in 2D) for the steel-concrete connection: JOINT_BA
Date:
09/09/05
Author (S):
S. MICHEL-PONNELLE, NR. DOMINGUEZ
Key
:
R7.01.21-A
Page
:
4/26
Manual of Reference
R7.01 booklet: Modelings for the Civil Engineering and the géomatériaux ones
HT-66/05/002/A
The connection will undergo a degradation different according to the type of loading applied, that is to say monotonous,
that is to say cyclic. In addition, among the most important parameters which influence the behavior of
the connection, one can quote:
· characteristics of the loading,
· geometrical characteristics of the steel bar,
· spacing between active bars,
· characteristics of the concrete,
· containment by passive reinforcement,
· side pressure.
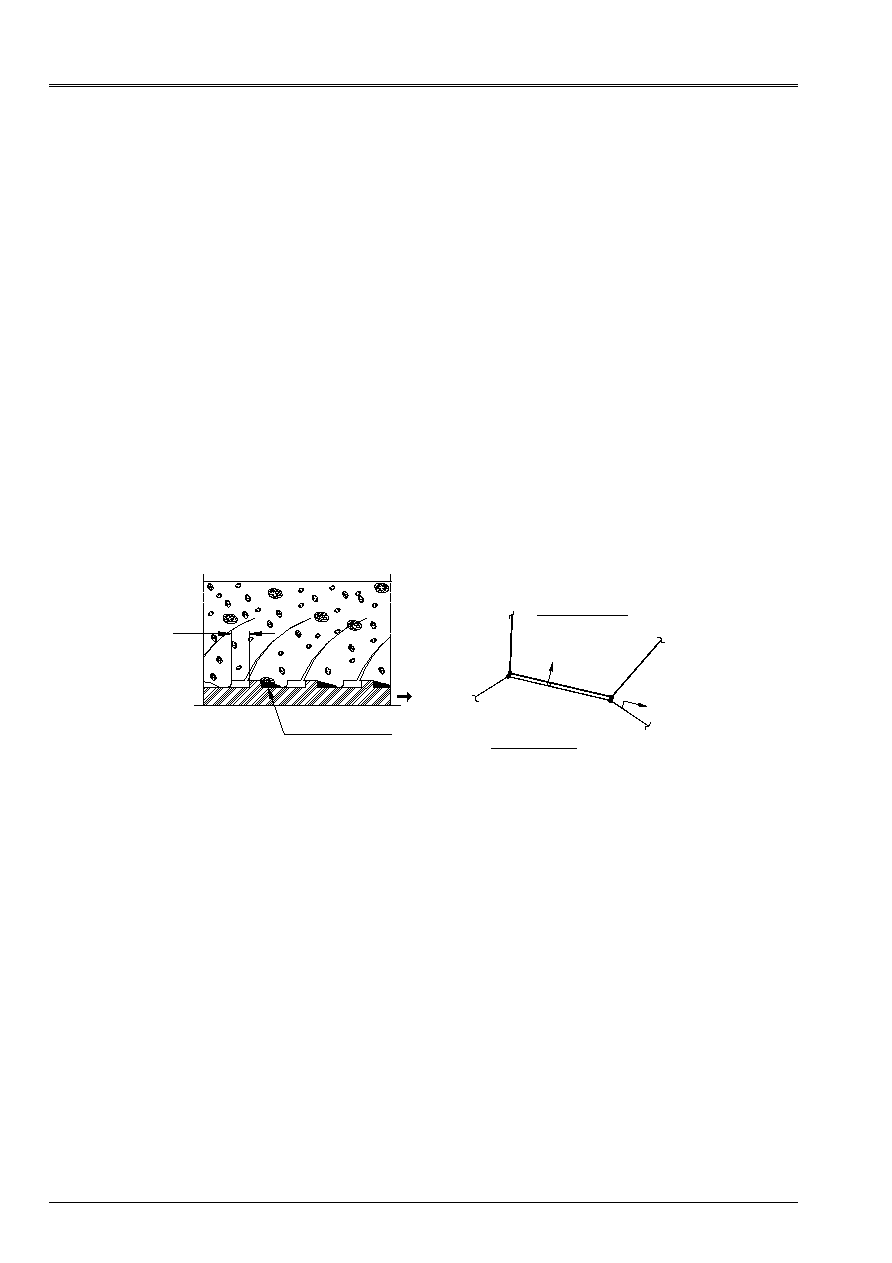
At the time of the study of a cylindrical bar embedded in an infinite medium, one can identify the surface of
discontinuity where one will place the linkage effects, which develops in a certain concrete area
fissured and crushed around the steel bar. At a given moment, this surface will correspond to
cylindrical fissure created during the coalescence of the fissures of shearing. By looking at the network
fissures, one can suppose that, in ideal conditions, the plan of cracking is always
perpendicular (normal direction) on the surface of the bar and parallel (tangential direction) with sound
longitudinal axis (see [Figure 2-a]). That enables us to project the components of displacement on
normal and tangential direction of the plan of cracking, and consequently to obtain the deformations
and corresponding stresses.
F
crushed concrete
slipped
Sd
A1
N
A2
BODY B
B1
T
B2
BODY A
Appear 2-a: real description of the phenomenon of connection and simplification finite elements:
co-ordinates in the local reference mark of the element of interface used like support of law JOINT_BA

Code_Aster
®
Version
7.4
Titrate:
Law of behavior (in 2D) for the steel-concrete connection: JOINT_BA
Date:
09/09/05
Author (S):
S. MICHEL-PONNELLE, NR. DOMINGUEZ
Key
:
R7.01.21-A
Page
:
5/26
Manual of Reference
R7.01 booklet: Modelings for the Civil Engineering and the géomatériaux ones
HT-66/05/002/A
3 Writing
theoretical
The formulation presented here was developed within the framework of the thermodynamics of the processes
irreversible; it gives the constitutive relation between the normal effort, the shear stress and it
slip by considering the influence of the cracking of the concrete, friction and the various couplings
in the phenomenon. For that, the constitutive relations which connect the tensor of the stresses and it
tensor of the deformations must include:
·
the cracking of material of interface by shearing
·
inelastic deformations because of the slip
·
the behavior hysteretic due to friction
·
coupling between the tangential answer and the normal stresses
3.1
Presentation of the model
One places oneself within the framework of a plane formulation in 2D, in the definite local reference mark [Figure 2-a].
tensors of the stresses
and of the deformations
are written:
=
0
NR
and
=
0
NR
éq 3.1-1
where
NR
is the normal stress and
is the tangential stress of the element of interface;
NR
corresponds to the normal deformation and
with the tangential deformation. Normal deformation
in the tangential direction with the interface is regarded as null. This mode of deformation for
an element of adherence is with null deformation energy.
Normal and tangential behaviors being regarded as uncoupled on the level from the state, it
thermodynamic potential obtained starting from the free energy of Helmholtz is expressed way
following:
[
(
)
+
+
-
-
-
+
=
NR
NR
NR
NR
NR
E
E
D
1
2
1
(
)
(
)
(
)
]
()
Z
G
G
F
T
T
T
F
T
T
T
T
T
D
D
1
2
+
+
-
-
+
-
+
éq
3.1-2
where
is the density,
is the Young modulus,
NR
D
is the internal variable of normal damage
and
T
D
the variable interns tangential damage, both being related to cracking and
ranging between 0 and 1.
G
is the module of rigidity or shearing,
F
T
is the deformation
irreversible induced by slip with friction of the fissures,
is the internal variable
of kinematic work hardening,
is a parameter material and
Z
, the variable of pseudo “work hardening
isotropic “by damage, with its function of consolidation
()
Z
.
-
and
+
define
respectively positive and negative parts of the tensor considered.
One can notice in the equation [éq 3.1-2] that in the normal direction, the damage will be
activated during the appearance of the positive deformations produced by forces of traction, while if
the deformations are negative because of the effects of compression, the behavior will remain
rubber band. With regard to the tangential part of the behavior, one can recognize a coupling
conventional élasticitéendommagement as well as a new term allowing to associate the state
elasticity-endommageable, a state of slip with friction. Coupling between slip and
cracking is possible thanks to the presence of the variable of damage like multiplier
in the second element of the right part of the equation [éq 3.1-2].

Code_Aster
®
Version
7.4
Titrate:
Law of behavior (in 2D) for the steel-concrete connection: JOINT_BA
Date:
09/09/05
Author (S):
S. MICHEL-PONNELLE, NR. DOMINGUEZ
Key
:
R7.01.21-A
Page
:
6/26
Manual of Reference
R7.01 booklet: Modelings for the Civil Engineering and the géomatériaux ones
HT-66/05/002/A
The laws of state are obtained classically by derivation of the thermodynamic potential, and thus
allow to define the associated thermodynamic variables. The normal stress is expressed
like:
(
)
>
-
=
=
0
D
1
0
NR
NR
NR
NR
NR
NR
NR
E
E
if
if
éq
3.1-3
and the total tangential stress like:
(
)
fT
T
T
T
T
T
T
G
G
-
+
-
=
=
D
)
D
1
(
éq
3.1-4
One can also define the tangential stress due to the slip with friction (deformation
S
):
(
)
fT
T
T
fT
fT
G
-
=
-
=
D
éq
3.1-5
Note:
Such a formulation moves away amply from a conventional formulation of coupling plasticity
damage. The assumption bringing to the introduction of the damage into the stress
by slip bases itself on an experimental observation which is that all the phenomena
inelastic in a fragile material come from the growth of the fissures.
The rate of energy restored by damage-friction can be written like:
(
) (
)
(
)
fT
T
fT
T
fT
T
T
T
T
G
G
2
1
2
1
D
D
+
-
=
-
-
=
-
=
-
-
éq
3.1-6
In this last expression,
T
D
corresponds to the rate of energy restored by damage and
fT
at the rate of energy restored by friction of the fissures.
The law of state of kinematic work hardening brings to the definition of the stress of recall:
=
=
éq
3.1-7
Concerning the law of work hardening of the isotropic damage, it is expressed by:
()
Z
Z
'
=
=
éq 3.1-8

Code_Aster
®
Version
7.4
Titrate:
Law of behavior (in 2D) for the steel-concrete connection: JOINT_BA
Date:
09/09/05
Author (S):
S. MICHEL-PONNELLE, NR. DOMINGUEZ
Key
:
R7.01.21-A
Page
:
7/26
Manual of Reference
R7.01 booklet: Modelings for the Civil Engineering and the géomatériaux ones
HT-66/05/002/A
It is necessary for us now to clarify in a more detailed way the evolution of the mechanism
of damage in the connection, in other words to specify the expression of
()
Z
. For weak
value of damage, the mechanism which prevails is the interaction of the concrete with the ribs of
the steel bar, while for a value much larger, it is friction between the concrete and
the steel which prevails. During the evolution of the damage, 2 main phases could be
identified:
· the first phase corresponds to a stable growth of transverse fissures related to
presence of ribs on steel (positive apparent work hardening of the law of evolution),
· the second does not utilize any more but the coalescence of these transverse fissures bringing to
not to more consider but the mechanisms of friction (negative work hardening towards a stress
of friction residual).
3.2
Analyze damage in the tangential direction
The law of evolution of the damage is divided into three stages:
1) area of perfect adherence,
2) area of passage of small deformations to the great slips,
3) area of maximum resistance of the connection and degradation until residual resistance
ultimate.
To identify these areas, two thresholds are established:
· the threshold of perfect adherence
1
T
,
· the threshold of continuity before coalescence of the fissures
2
T
.
Thus, by taking again the expressions related to the damage with knowing that of the rate of refund
of energy [éq 3.1-6] and that of the variable interns associated with isotropic work hardening [éq 3.1-8], one can
to note:
· a true separation between L `damage and the friction of the fissures (what allows
to amend only the law of evolution of the damage without affecting the part
“friction”),
· the partition in two parts of isotropic work hardening since one has two different stages in
the damage.
From now on we will write for work hardening related to the variable of damage:
()
<
<
=
=
=
T
T
T
T
T
T
T
T
T
Z
Z
2
2
1
2
1
1
,
,
'
if
if
éq
3.2-1
Components
1
T
and
2
T
express themselves in the following way:
(
)
2
1
D
1
1
1
1
ln
2
1
+
+
=
T
T
T
T
T
T
Z
G
With
éq
3.2-2
+
-
+
=
T
T
T
T
T
Z
Z
With
1
1
D
2
2
2
éq
3.2-3
Code_Aster
®
Version
7.4
Titrate:
Law of behavior (in 2D) for the steel-concrete connection: JOINT_BA
Date:
09/09/05
Author (S):
S. MICHEL-PONNELLE, NR. DOMINGUEZ
Key
:
R7.01.21-A
Page
:
8/26
Manual of Reference
R7.01 booklet: Modelings for the Civil Engineering and the géomatériaux ones
HT-66/05/002/A
The function threshold is also defined
T
D
who depends on
T
D
and which S `writes like:
(
)
0
1
D
D
+
-
=
T
T
T
T
éq
3.2-4
The thresholds which manage the law of evolution of the damage are also expressed in terms of
T
D
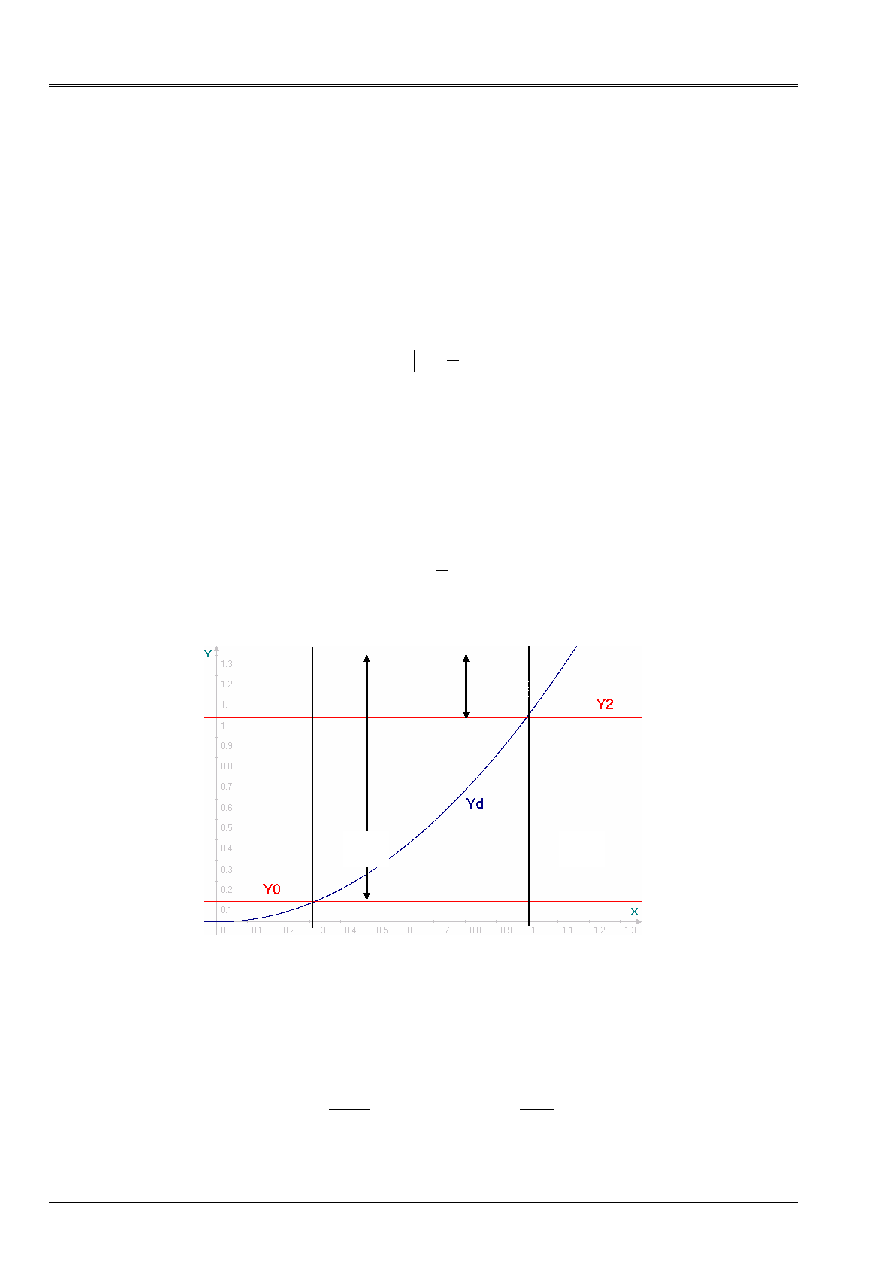
(see [Figure 3.2-a]). The first expression corresponds to the threshold of perfect adherence and S `written:
1
1
1
2
1
T
T
T
elas
T
G
=
=
éq
3.2-5
Where
1
T
is the initial threshold of damage defined according to the limiting deformation of adherence
perfect
1T
, which will correspond to the limiting deformation of shearing or traction of the front concrete
the initialization of the damage. In addition,
2
T
is the threshold of initiation of coalescence of
microscopic cracks which is defined according to the initial tangential deformation of the great slips
2
T
:
2
2
2
2
1
T
T
T
G
=
éq
3.2-6
t2
t0
1
2
Appear 3.2-a: construction of the functions thresholds in terms of energy
The laws of evolution of the internal variables within the framework of the standard associated laws allow
to obtain the derivative of the multiplier of damage
D
:
D
D
D
D
D
D
D
D
·
·
·
·
·
·
-
=
=
=
=
Z
and
éq 3.2-7
0
2

Code_Aster
®
Version
7.4
Titrate:
Law of behavior (in 2D) for the steel-concrete connection: JOINT_BA
Date:
09/09/05
Author (S):
S. MICHEL-PONNELLE, NR. DOMINGUEZ
Key
:
R7.01.21-A
Page
:
9/26
Manual of Reference
R7.01 booklet: Modelings for the Civil Engineering and the géomatériaux ones
HT-66/05/002/A
By using the condition of consistency in addition, one obtains the expression of the damage:
(
)
*
2
exp
1
D
D
1
D
D
1
D
1
-
-
=
T
B
T
T
T
T
T
T
G
With
1
-
+
+
T
B
T
T
T
With
D
1
D
D
2
1
1
2
éq 3.2-8
In this expression, one can identify the part which corresponds to the area of the passage of small
deformations with the great slips with two parameters:
T
With
D
1
and
T
B
D
1
, as well as the part
of damage finale in mode 2, with the parameters
T
With
D
2
and
T
B
D
2
. It should be noted that the relation
-
1
D
T
T
is managed by a function of Macaulay, i.e. this difference in energy must
to be always positive or null.
The functions which manage isotropic work hardening in the tangential direction are expressed like:
;
Y
Y
Z
1
D
1
T
T
T
-
=
éq 3.2-9
<
-
<
=
T
T
T
T
T
T
T
T
D
2
2
D
2
D
1
2
,
0
if
if
,
éq
3.2-10
According to these expressions, one can notice that
2
T
is not taken into account in the area of
transition from the small deformations to great slips.
3.3
Analyze damage in the normal direction
The two most important mechanisms which can appear on the normal direction are it
detachment between the concrete and the bars of steel, and the penetration of the reinforcement in the body of
concrete. These two conditions can be interpreted respectively like an opening or one
closing of fissure, and can be described by a particular law of behavior in
normal direction uncoupled from the tangential behavior.
In order to simplify the resolution for compression between surfaces, one decided to allow small
penetration between those, which implies that
0
NR
, and by adopting a law of behavior
rubber band, one will have:
0
=
-
NR
NR
NR
E
if
éq
3.3-1
The case of the decoherence of the interface can be described by a behavior endommageable in
normal direction, is:
(
)
0
D
1
>
-
=
+
NR
NR
NR
NR
E
if
éq
3.3-2

Code_Aster
®
Version
7.4
Titrate:
Law of behavior (in 2D) for the steel-concrete connection: JOINT_BA
Date:
09/09/05
Author (S):
S. MICHEL-PONNELLE, NR. DOMINGUEZ
Key
:
R7.01.21-A
Page
:
10/26
Manual of Reference
R7.01 booklet: Modelings for the Civil Engineering and the géomatériaux ones
HT-66/05/002/A
with
NR
D
scalar variable of the damage in the normal direction, calculated with the expression
following:
<
-
+
=
+
NR
NR
B
NR
NR
NR
NR
NR
NR
NR
With
1
1
D
D
1
D
1
1
0
D
if
if
éq
3.3-3
In this expression, two parameters material,
NR
With
D
and
NR
B
D
, control decoherence by
the damage in traction of the concrete. In addition,
1
NR
is the threshold of damage defined in
term of energy, are equivalent to the elastic threshold in the normal direction
NR
elas
and which is expressed
like:
1
1
1
2
1
NR
NR
NR
elas
NR
E
=
=
éq
3.3-4
1
NR
being limiting deformation of perfect adherence, which corresponds to the limiting deformation of the concrete in
traction before the initialization of the damage. It should be mentioned that when the detachment or
the opening of fissure reaches the maximum value of resistance to traction, no force of
shearing will not have to be transmitted between two materials: it east is the single condition in
which the scalar variable of damage in the tangential direction becomes 1 because of
the damage in the normal direction
3.4 Analyze contribution of the friction of fissures by
slip
With regard to the part “slip” of the formulation, one supposes that it has a behavior
pseudo-plastic, with nonlinear kinematic work hardening. Initially introduced by Armstrong &
Frederick, 1966, cf [bib1], nonlinear kinematic work hardening makes it possible the formulation to surmount
the main disadvantage of the kinematic law of work hardening of Prager, namely, the linearity of the law
of state which connects the forces associated with kinematic work hardening. Here, the nonlinear terms are
additions in the potential of dissipation. The criterion of slip takes the conventional form of
function threshold of Drucker-Prager which takes into account the effect of radial containment on the slip:
0
1
+
-
=
I
C
fT
F
éq
3.4-1
Here
is the stress of recall,
C
is a parameter related to material, translating the influence of
containment, while
1
I
corresponds to the first invariant of the tensor of the stresses, which for our
case is expressed like:
[]
NR
I
=
=
3
1
3
1
1
Tr
éq
3.4-2
Code_Aster
®
Version
7.4
Titrate:
Law of behavior (in 2D) for the steel-concrete connection: JOINT_BA
Date:
09/09/05
Author (S):
S. MICHEL-PONNELLE, NR. DOMINGUEZ
Key
:
R7.01.21-A
Page
:
11/26
Manual of Reference
R7.01 booklet: Modelings for the Civil Engineering and the géomatériaux ones
HT-66/05/002/A
In addition, the initial threshold for the slip is 0. Moreover, by considering the principle of dissipation
figure maximum, the laws of evolution can be derived from the expression of the plastic potential which
is:
2
1
4
3
+
+
-
=
has
I
C
fT
p
F
éq
3.4-3
Where
has
is a parameter material. It should be mentioned that the quadratic term in
allows
to introduce the non-linearity of kinematic work hardening. Laws of evolution for the deformation of
slip as for kinematic work hardening take the following forms:
=
=
·
·
·
·
p
fT
p
fT
F
F
F
F
and
éq 3.4-4
The multiplier of slip
F
·
is calculated numerically by imposition of the condition of
consistency.
3.5
Summary of the equations
We show here, a summary of the equations which constitute the law of behavior of the connection
steel-concrete:
Free energy
of Helmholtz
(
)
[
(
)
(
)
(
)
]
()
Z
G
G
E
E
F
T
T
T
F
T
T
T
T
T
NR
NR
NR
NR
NR
H
D
.
D
1
D
1
.
2
1
.
2
+
+
-
-
+
-
+
-
+
=
+
+
-
-
Function threshold
(
)
0
.
X
;
0
Z
Y
Y
1
F
1
D
D
+
-
=
+
-
=
I
C
fT
T
T
T
T
Laws of state
(
)
(
)
(
)
(
)
F
T
T
T
F
F
T
T
T
T
T
T
NR
NR
NR
NR
NR
NR
G
G
G
E
E
-
=
-
+
-
=
>
-
=
D
.
;
D
.
D
1
;
0
.
.
D
1
0
.
if
if
Dissipation
(
)
()
Z
Z
F
'
D
H
Z
;
X
;
Y
Y
D
Y
=
=
=
=
+
-
=
-
=
-
Laws
of evolution
X
.
;
.
;
Z
.
;
Y
.
D
F
F
F
F
D
D
D
D
D
D
D
=
=
-
=
=
=
=
p
fT
p
F
T
Z
&
&
&
&
&
&
&
&
&
&

Code_Aster
®
Version
7.4
Titrate:
Law of behavior (in 2D) for the steel-concrete connection: JOINT_BA
Date:
09/09/05
Author (S):
S. MICHEL-PONNELLE, NR. DOMINGUEZ
Key
:
R7.01.21-A
Page
:
12/26
Manual of Reference
R7.01 booklet: Modelings for the Civil Engineering and the géomatériaux ones
HT-66/05/002/A
3.6
Form of the tangent matrix
In order to ensure the robustness and the effectiveness of the model in the numerical establishment and for the analysis
total of the massive structures, it is necessary to calculate the tangent matrix, which can be given with
to leave the following expression:
·
·
=
T
T
éq 3.6-1
After some analytical calculations, one can deduce the expression from the tangent module while using
condition of consistency and respective laws of evolution:
(
)
(
)
(
)
(
)
(
)
(
)
(
)
+
-
=
D
1
)
(
1
H
2
2
p
T
p
T
T
fT
T
T
G
G
G
F
F
F
F
éq
3.6-2
With
T
T
T
T
T
T
T
G
H
H
G
F
H
G
F
H
G
F
G
-
-
=
=
2
D
D
'
'
'
D
)
(
éq
3.6-3
Where
H
G
F
and
,
are the following functions, obtained thanks to [éq 3.2-8]:
T
T
F
D
1
=
éq 3.6-4
(
)
-
=
T
B
T
T
T
G
With
G
D
1
D
D
1
2
exp
1
éq
3.6-5
T
B
T
T
T
With
H
D
1
D
D
2
1
2
+
-
+
=
éq
3.6-6
Note:
In practice in Aster, the tangent matrix was not established, only the secant matrix is
used either
-
-
=
)
1
(
0
0
)
1
(
T
NR
D
G
D
E
H
.

Code_Aster
®
Version
7.4
Titrate:
Law of behavior (in 2D) for the steel-concrete connection: JOINT_BA
Date:
09/09/05
Author (S):
S. MICHEL-PONNELLE, NR. DOMINGUEZ
Key
:
R7.01.21-A
Page
:
13/26
Manual of Reference
R7.01 booklet: Modelings for the Civil Engineering and the géomatériaux ones
HT-66/05/002/A
4 Integration
numerical
Separation in two parts in the formulation: damage slip, allows us
to treat each one of it separately. Thus, the integration of the damage part is carried out of
explicit way by the definition of two surfaces threshold. On the other hand, the part “slip” is solved
in an implicit way by a conventional method with knowing the algorithm of the type “return-mapping”
proposed by Ortiz & Simo, cf [bib4], which will ensure the effective convergence of way.
4.1 Calculation of the part “friction of the fissures” with a method
of implicit integration
The effects on the connection associated with the phenomenon of friction with the fissures can be calculated in
the framework of a behavior pseudo-plastic with a nonlinear kinematic work hardening. For
the establishment with the method of integration suggested, we will carry out a linearization of
function threshold around the current values of the variables intern associated. With the iteration (i+1),
surface threshold is written:
(
)
0
:
:
)
(
)
1
(
)
(
)
(
)
1
(
)
(
)
(
-
+
-
+
=
+
+
I
I
I
I
fT
I
fT
fT
I
I
F
F
F
F
éq
4.1-1
According to the equations [éq 3.1-7], [éq 3.1-8], and [éq 3.6-5], one a:
-
=
=
·
·
·
p
F
F
éq
4.1-2
fT
p
T
fT
T
fT
G
G
-
=
-
=
·
·
·
F
F
D
D
éq
4.1-3
That one can discretize in the following way:
)
(
)
1
(
-
=
=
-
=
+
p
I
I
F
F
éq
4.1-4
fT
p
T
fT
T
I
fT
I
fT
fT
G
G
-
=
-
=
-
=
+
F
F
D
D
)
(
)
1
(
éq
4.1-5
By combining these expressions with the expression of surface threshold and by writing that
F
is equal to
zero, one can deduce the increment from multiplier
F
with each iteration
I
:
)
(
)
(
)
(
)
(
)
(
D
I
p
I
I
fT
p
T
I
fT
I
G
+
=
F
F
F
F
F
F
éq
4.1-6
After obtaining the value of
F
, one can substitute it in the equations [éq 4.1-4] and [éq 4.1-5]
in order to bring up to date the thermodynamic forces
fT
and
. The iterations will have to continue until
moment when the condition of consistency is checked.

Code_Aster
®
Version
7.4
Titrate:
Law of behavior (in 2D) for the steel-concrete connection: JOINT_BA
Date:
09/09/05
Author (S):
S. MICHEL-PONNELLE, NR. DOMINGUEZ
Key
:
R7.01.21-A
Page
:
14/26
Manual of Reference
R7.01 booklet: Modelings for the Civil Engineering and the géomatériaux ones
HT-66/05/002/A
4.2
The algorithm of resolution
In a general way, one seeks to check the balance of the structure at every moment, in a form
incremental. As clarified previously, for the damage a simple scalar equation
allows to obtain the corresponding value, which makes it possible to avoid a recourse to the iterative methods.
On the other hand, an iterative method is applied for integration of the friction part of the fissures.
Then, the algorithm is as follows:
(I) Reactualization
geometrical:
()
()
T
S
N
T
1
N
T
U
+
=
+
(II) Prediction
rubber band:
()
()
N
F
T
0
1
N
F
T
=
+
)
(
;
()
()
()
1
N
F
T
1
N
T
0
1
N
E
T
+
+
+
-
=
)
(
;
N
0
1
N
=
+)
(
;
()
(
)
)
(
)
(
)
(
0
1
N
0
1
N
E
T
0
1
N
+
+
+
=
,
(III) Evaluation of
threshold:
()
?
)
(
0
0
1
N
+
F
if SO, end of the cycle; so NOT, beginning of the iterations
YES:
()
()
)
(
0
1
N
F
T
1
N
F
T
+
+
=
;
()
()
)
(
0
1
N
E
T
1
N
E
T
+
+
=
;
)
(
0
1
N
1
N
+
+
=
;
)
(
0
1
N
1
N
+
+
=
NOT:
0
I
=
(iv) Correction
plastic:
()
()
(
)
()
(
)
()
(
)
()
(
)
()
I
N
p
in
I
N
fT
p
T
I
N
fT
in
F
G
1
F
1
F
1
F
1
F
1
F
X
/
.
.
X
/
/
D
.
/
+
+
+
+
+
+
=
()
()
(
)
()
(
)
()
I
p
I
fT
p
T
I
N
I
N
G
X
/
.
.
/
.
.
D
.
F
F
F
F
1
1
1
-
-
=
+
+
+
(
)
)
(
)
(
)
(
I
p
I
1
N
1
I
1
N
+
=
+
+
+
F
F
(v) Checking of
convergence:
()
()
?
)
(
)
(
0
1
N
1
I
1
N
TOL
+
+
+
F
F
if SO, end of the cycle; so NOT, to continue the iterations in (iv)
YES:
)
(
1
I
1
N
1
N
+
+
+
=
;
)
(
1
I
1
N
1
N
+
+
+
=
;
()
(
)
1
N
1
N
E
T
1
N
E
T
+
+
+
=
,
;
()
()
()
1
N
E
T
1
N
T
1
N
F
T
+
+
+
-
=
NOT:
1
I
I
+
=

Code_Aster
®
Version
7.4
Titrate:
Law of behavior (in 2D) for the steel-concrete connection: JOINT_BA
Date:
09/09/05
Author (S):
S. MICHEL-PONNELLE, NR. DOMINGUEZ
Key
:
R7.01.21-A
Page
:
15/26
Manual of Reference
R7.01 booklet: Modelings for the Civil Engineering and the géomatériaux ones
HT-66/05/002/A
4.3
Variables intern model
We show here the internal variables stored in each point of Gauss in the implementation of
model:
Number of
variable
intern
Feel physical
1
NR
D
: Scalar variable of the damage in the normal direction
2
T
D
: Scalar variable of the damage in the tangential direction
3
1
T
Z
: Scalar variable of isotropic work hardening for the damage in mode 1
4
2
T
Z
: Scalar variable of isotropic work hardening for the damage in mode 2
5
F
T
: Deformation of slip cumulated by friction of the fissures
6
: Value of kinematic work hardening by friction of the fissures
5
Parameters of the law
The law of behavior presented here is controlled by 14 parameters, of which 3 manage the answer in
the normal direction and the others affect the response in the tangential direction. In addition, it
Young modulus is recovered starting from the elastic data provided by the operator ELAS, who must
to always appear in the command file.
These parameters, or the analytical expressions which make it possible to obtain them, were obtained or
determined starting from the digital simulation of the experimental tests carried out by Eligehausen and
Al, 1983, cf [bib3]. The realization of multiple simulations made it possible to determine a relation enters
geometrical and material characteristics of materials in question (steel and concrete) and them
parameters which manage the model of the interface.
5.1
Initial parameters
5.1.1 The parameter “hpen”
The element gasket functioning on the concept of jump of displacement, it is necessary to introduce one
dimension characteristic of the area of degraded interface allowing to define the concept of
deformation in the interface. With this intention it was introduced the principle of penetration between surfaces:
parameter “hpen” makes it possible to define this area surrounding the bar of steel. This parameter corresponds
with the possible maximum penetration which depends on the thickness of the compressed concrete - crushed. Into same
time, “hpen” manages the dissipation of energy in the element as well as the kinematics of the slip.
In order to give a reference to the user for the choice of this parameter, one proposes to calculate it with
to leave the diameter of the bar D
B
and the relative surface of the ribs
Sr
defined by:
C
D
F
K
B
R
Sr
=
sin
éq
5.1.1-1
where
K
is the number of ribs on the perimeter;
R
F
the transverse surface of a rib;
is the angle
between the rib and the axis longitudinal of the steel bar; and
C
is the measured distance between ribs
center in center. Finally, “hpen” will be calculated with the expression:
Sr
B
PEN
D
H
=
éq
5.1.1-2

Code_Aster
®
Version
7.4
Titrate:
Law of behavior (in 2D) for the steel-concrete connection: JOINT_BA
Date:
09/09/05
Author (S):
S. MICHEL-PONNELLE, NR. DOMINGUEZ
Key
:
R7.01.21-A
Page
:
16/26
Manual of Reference
R7.01 booklet: Modelings for the Civil Engineering and the géomatériaux ones
HT-66/05/002/A
According to Eligehausen and Al, the reinforcements usually used in the United States have values of
Sr
between 0.05 and 0.08. For the smooth bars, since one needs a small value for
“hpen”, one proposes values of
Sr
between 0.005 and 0.02.
The following table gives the values of “hpen” according to the diameter of the bar:
Diameter (mm)
Relative surface
Hpen (mm)
Description
8 0.01
(0.08)
0.1
Smooth commercial bar
8
0.08
0.64
Ribbed commercial bar
20
0.08
1.50
Ribbed commercial bar
25
0.08
2.00
Ribbed commercial bar
32
0.08
2.54
Ribbed commercial bar
The unit of “hpen” must of course correspond to the unit used for the mesh.
5.1.2 The parameter G or module of rigidity of the connection
Generally, because of difficulty in measuring the deformations by shearing, the module of
rigidity of a material is calculated starting from Young and the Poisson's ratio modulus, parameters
currents obtained in experiments. However, for our case, the interface is a pseudo-material
whose characteristics must depend on the properties corresponding to materials in contact,
steel and concrete. Since the material which one expects to damage is the concrete, one proposes
to initially use for the connection the same value of
G
that for the studied concrete but it can be
higher up to a value similar to the value of the Young modulus
E
, when one increases
value of “hpen”. In the case of reinforcements with rigidities higher than those of the bars
commercial current (because of a provision or special geometry of the ribs), one can make
a correction of the value chosen, by multiplying the module of rigidity by a coefficient of correction
calculated starting from the relative surfaces of the commercial bars, with the expression:
(
)
(
)
COM
SR
SR
ARM
bar
bar
C
=
éq
5.1.2-1
Then, the module of rigidity of the connection G will be:
concrete
ARM
bound
G
C
G
=
éq
5.1.2-2
In the last expressions,
bound
G
is the module of rigidity of the connection;
concrete
G
is the module of
rigidity of the concrete;
ARM
C
is the coefficient of correction per reinforcement;
(
)
bar
SR
, relative surface of
ribs of the bar concerned; and
(
)
COM
SR
bar
, relative surface of the ribs of the bar
commercial of the same diameter (preferably, 0.08).

Code_Aster
®
Version
7.4
Titrate:
Law of behavior (in 2D) for the steel-concrete connection: JOINT_BA
Date:
09/09/05
Author (S):
S. MICHEL-PONNELLE, NR. DOMINGUEZ
Key
:
R7.01.21-A
Page
:
17/26
Manual of Reference
R7.01 booklet: Modelings for the Civil Engineering and the géomatériaux ones
HT-66/05/002/A
5.2
Parameters of damage
5.2.1 Limit of elastic strain
1T
or threshold of perfect adherence
To define the threshold of perfect adherence, it is considered that the damage by shearing must
to initiate itself at the time of the going beyond of a certain threshold of deformation. So one proposes to adopt them
deformations limit concrete in traction, i.e., between 1x10
- 4
and 0.5x10
- 3
, which corresponds to
shear stresses between 0.5 and 4 MPa in perfect adherence.
5.2.2 The parameter of damage A
1DT
for the passage of the small deformations
with the great slips
In this area, the law of evolution of the damage is expressed in term of deformations and its
construction depends on the definite elastic slope for the linear behavior (stress on
shearing vs. deformation) in the area of perfect adherence: this parameter controls the value of
the stress compared to the slip in the passage of small deformations to large
slips.
The determination of the value of this parameter is a key and delicate point model, since the evolution
damage must be carried out with certain conditions noticed by several researchers;
for example:
·
the resistance of the connection is directly proportional to the compressive strength of
concrete. However, as the resistance of the concrete is increased, it
behavior becomes more rigid, bringing to the brittle fracture of the connection,
·
the particular rigidity of the reinforcement, which is related on the diameter and the quantity of the ribs on
surface, must increase the resistance of the connection,
·
the relation between the moduli of elasticity of two materials concerned must manage directly
the kinematics of the connection.
From the digital simulations that one carried out, one observed that this value is located
between a minimum of 1 and one maximum of 5, and which it will have to be adjusted according to the test of
reference selected. Optionally, one proposes an expression which makes it possible to adopt an initial value
and which depends on the particular characteristics of materials:
(
)
B
has
SR
T
C
F
With
E
E
30
'
1
1
D
1
+
=
éq
5.2.2-1
In the last expression, E
B
will be calculated with the expression provided in the section A.2.1, 2 of
BAEL'91:
()
3
1
'
11000
E
C
F
B
×
=
éq
5.2.2-2
In the two last expressions, one a:
·
C
F
'
, compressive strength of the concrete in MPa;
·
has
E
, modulus of elasticity of steel, in MPa;
·
B
E
, modulus of elasticity of the concrete, in MPa;
·
Sr
, relative surface of the ribs of the bar concerned.
Code_Aster
®
Version
7.4
Titrate:
Law of behavior (in 2D) for the steel-concrete connection: JOINT_BA
Date:
09/09/05
Author (S):
S. MICHEL-PONNELLE, NR. DOMINGUEZ
Key
:
R7.01.21-A
Page
:
18/26
Manual of Reference
R7.01 booklet: Modelings for the Civil Engineering and the géomatériaux ones
HT-66/05/002/A
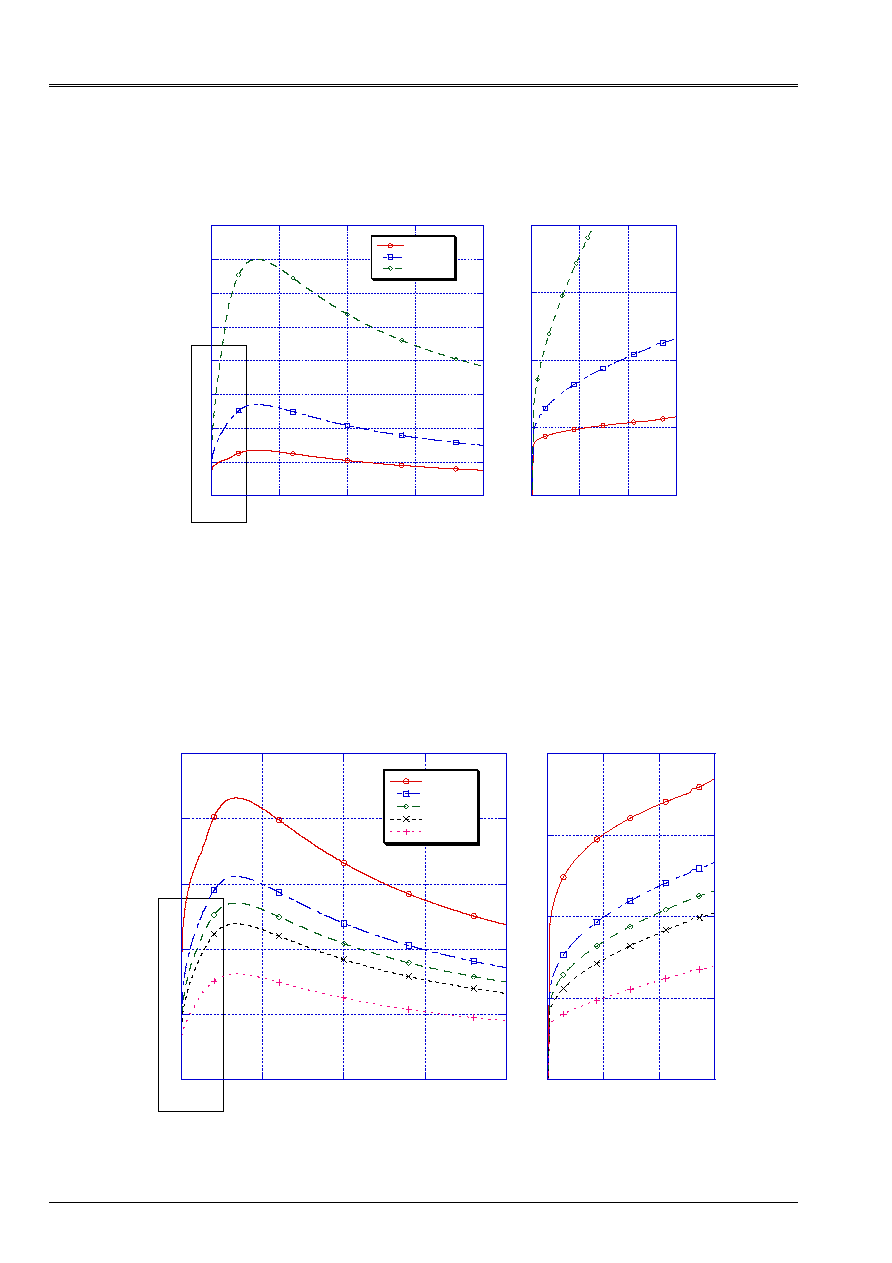
[Figure 5.2.2-a] gives some a graphic comparison.
0
5
10
15
20
25
30
35
40
0
0.5
1
1.5
2
COMPARISON OF A1DT
- Local Law of the connection -
ad1=1.0
ad1=2.19
ad1=3.8
S
X
Y (M
AP
)
-
contr
has
I
N
T
E
of
C
I
sai
L
L
E
m
ent
MT
O
-
defo EXY
0
5
10
15
20
0
0.05
0.1
0.15
SX
Y (
M
P
has
)
defo EXY
Appear 5.2.2-a: Comparison of
T
With
D
1
: growth of the resistance of the connection
5.2.3 The parameter of damage B
1DT
The purpose of this parameter is to soften the shape of the curve of behavior, like facilitating
transition from the elastic slope towards the nonlinear area. It can have a value included/understood enters
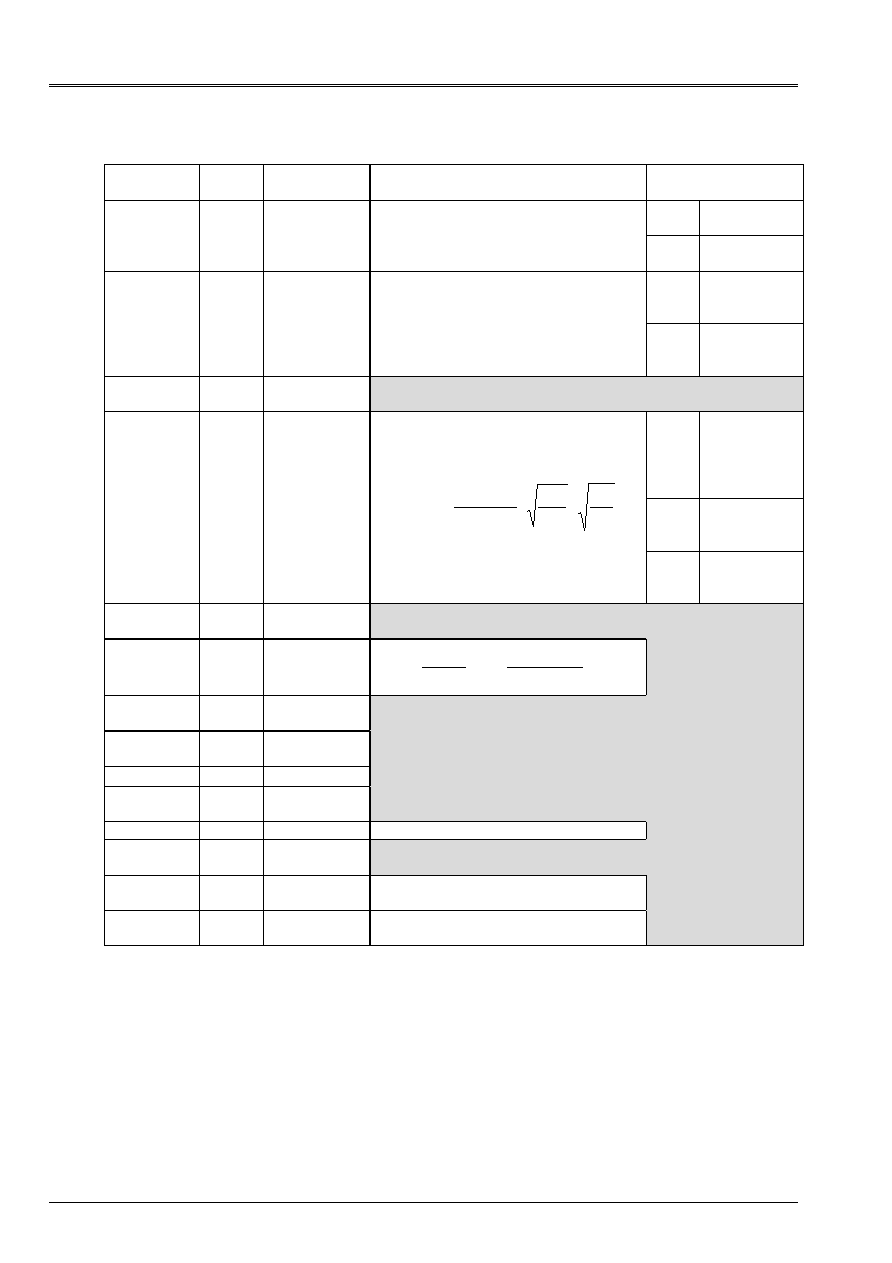
0.1 and 0.5 (never higher than 0.5 since it is the equivalent of the square root of the formula) .On can
to advise to adopt the value of 0.3 for ordinary calculations. (See [Figure 5.2.3-a]).
0
5
10
15
20
25
0
0.5
1
1.5
2
VARIATION DE Bd1
- Local Law of the connection -
Bd1=0.1
Bd1=0.2
Bd1=0.25
Bd1=0.3
Bd1=0.5
SXY (
M
AP)
-
Co
N
T
ruffle
I
N
T
E
D
E
Ci
its
I
L
L
E
m
E
NT MT
O
-
defo EXY
0
5
10
15
20
0
0.05
0.1
0.15
S
XY (M
AP
)
defo EXY
Appear 5.2.3-a: Comparison of
T
B
D
1
: Amendment of the curvature

Code_Aster
®
Version
7.4
Titrate:
Law of behavior (in 2D) for the steel-concrete connection: JOINT_BA
Date:
09/09/05
Author (S):
S. MICHEL-PONNELLE, NR. DOMINGUEZ
Key
:
R7.01.21-A
Page
:
19/26
Manual of Reference
R7.01 booklet: Modelings for the Civil Engineering and the géomatériaux ones
HT-66/05/002/A
5.2.4 Limit of deformation
2T
or threshold of the great slips
According to several authors, the great slips are overall higher 1 mm from displacement,
but that is an indicator which depends on the form and dimensions of the specimens tested; therefore, one
propose that this deformation never exceeds 1.00 (adimensional value). In way more
specify, one proposes to apply the following expression:
()
(
)
(
)
()
(
)
(
)
1.0
9
1
1
1
1
4
D
1
4
D
1
2
D
1
D
1
2
2
+
-
=
+
-
=
T
T
PEN
N
T
N
T
PEN
T
With
With
H
With
C
With
H
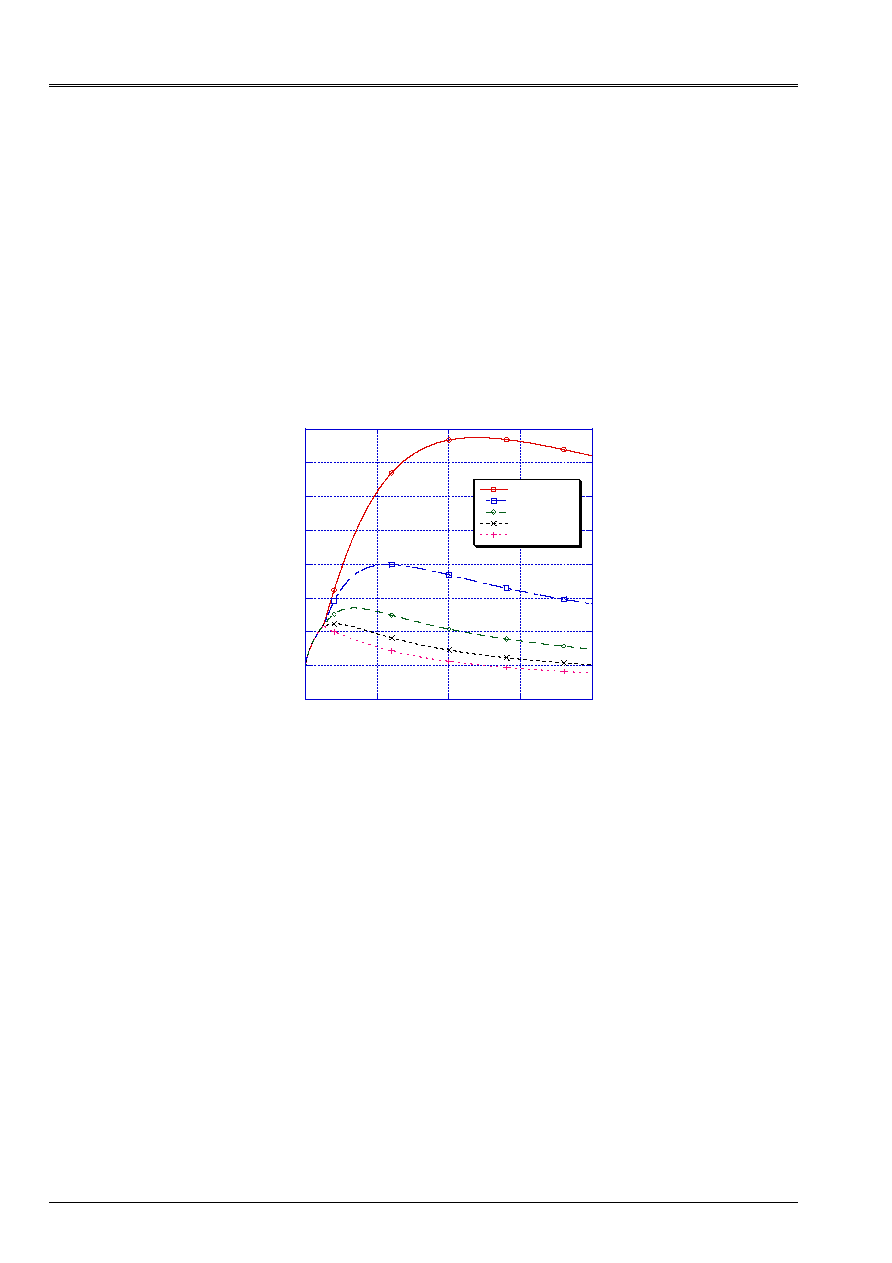
éq 5.2.4-1
In this expression, one applied a sigmoid function of which coefficients
C
and
N
allow
to adjust the kinematic effect of
T
With
D
1
on the slip, i.e., when the connection becomes more
resistant because of an increase in rigidity, the slip is reduced gradually. One adopted
values 9.0 and 4.0 respectively, but they are always optional.
The choice of the value of the limit of deformation
2
T
is very important because it introduces one more or less
great brittleness of the response by translation of the threshold of passage of the small deformations to large
slips. This brittleness is related to the stiffness of the concrete via the parameter
T
With
D
1
. It is necessary
to note that the following parameters which manage the damage must be also adjusted on the level
room to ensure the correct continuity of behavior in shearing of the connection and to thus be able
to obtain the desired or awaited response of a system real steel connection concrete.
Code_Aster
®
Version
7.4
Titrate:
Law of behavior (in 2D) for the steel-concrete connection: JOINT_BA
Date:
09/09/05
Author (S):
S. MICHEL-PONNELLE, NR. DOMINGUEZ
Key
:
R7.01.21-A
Page
:
20/26
Manual of Reference
R7.01 booklet: Modelings for the Civil Engineering and the géomatériaux ones
HT-66/05/002/A
5.2.5 The parameter of damage A
2DT
The damage, such as it was conceived in the model, obeys two laws of evolution which are
expressed using only one conventional scalar variable which will ensure the coherence of
the damage. The parameters of each of the 2 laws are independent and numerically
stable, but they are likely to generate serious errors in the continuity of the behavior
if one does not pay attention to the shape of the local curve stress-strain: to see the case of
curve shown in graphics of [Figure 5.2.5-a], with a value
T
With
D
2
= 1x10
- 3
MPa
- 1
. Us
let us not be able to propose an analytical relation for the choice of this parameter, but
the gained experience enables us to affirm that the value of this parameter must be included/understood enters
1x10
- 3
and 9x10
- 2
MPa
- 1
roughly.
0
5
10
15
20
25
30
35
40
0
0.5
1
1.5
2
COMPARISON OF A2DT
- Local Law of the connection -
Ad2 = 1e-3
Ad2 = 3rd-3
Ad2 = 6th-3
Ad2 = 9th-3
Ad2 = 1.2e-2
SX
Y
(
M
P
has
)
-
contr
has
I
N
T
E
of
C
I
sai
L
L
E
m
ent
MT
O
-
defo EXY
Appear 5.2.5-a: Comparison of
T
With
D
2
: damage and rupture of the connection
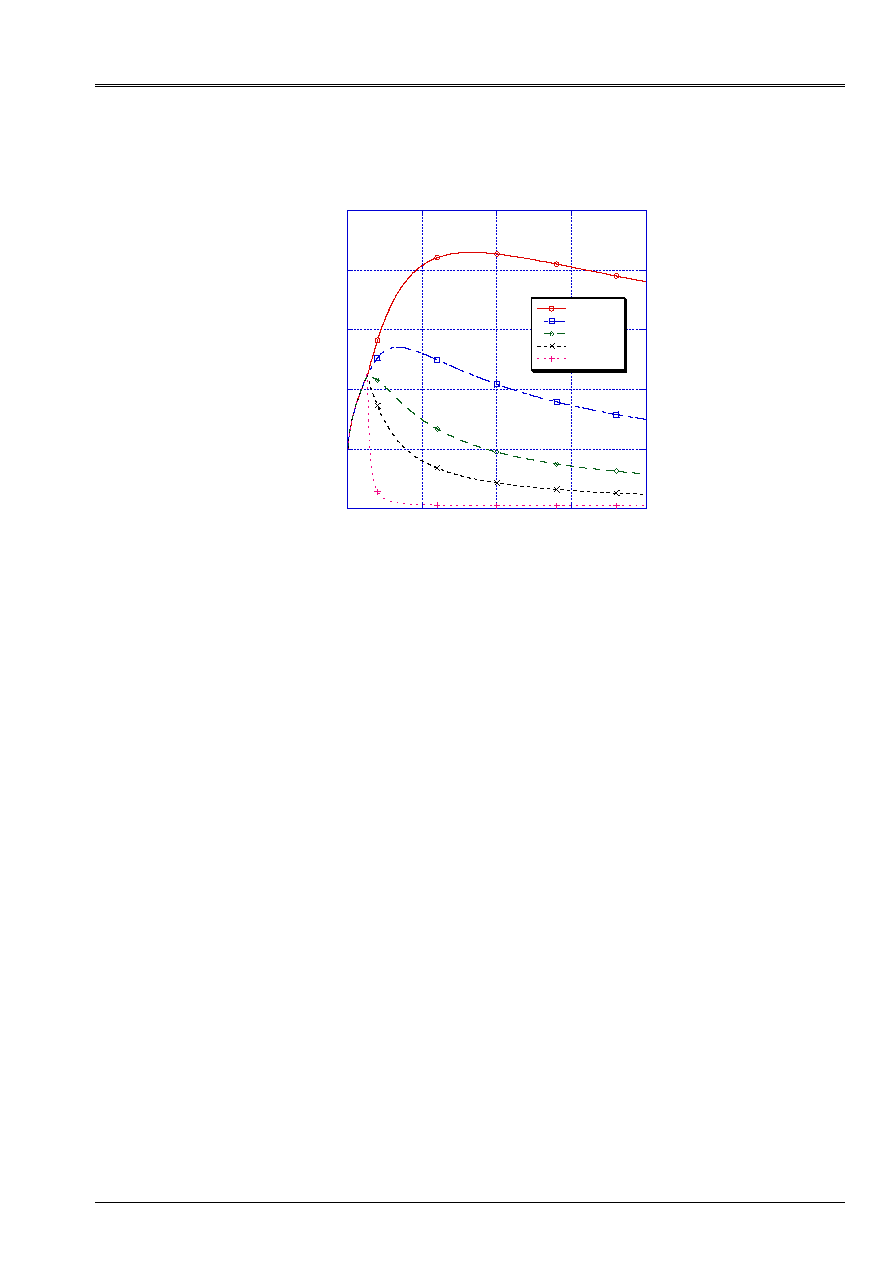
5.2.6 The parameter of damage B
2DT
This parameter, which supplements the law of evolution of damage in great slips, controls not
only growth of the resistance of the connection or shape of the curve of behavior to the peak
and in the area post-peak, but also the kinematics of the answer, which implies the determination of
slip for the maximum shear stress as well as the amplitude of the curve to the peak of
behavior. Then, although values of the parameters of damage
T
With
D
2
and
T
B
D
2
will have to adjust itself at the same time when one builds the curve of behavior of the connection in order to
to respect the continuity of the pace, one can say that the value of
T
B
D
2
is inversely proportional
the amplitude of slip at the top, i.e., a value of 0.8 allows great slips
broader in the node than a value of 1.2, for example.
For practical cases, one recommends to use a value ranging between 0.8 and 1.1 to reproduce
a coherent curve of behavior (See [Figure 5.2.6-a]).
Code_Aster
®
Version
7.4
Titrate:
Law of behavior (in 2D) for the steel-concrete connection: JOINT_BA
Date:
09/09/05
Author (S):
S. MICHEL-PONNELLE, NR. DOMINGUEZ
Key
:
R7.01.21-A
Page
:
21/26
Manual of Reference
R7.01 booklet: Modelings for the Civil Engineering and the géomatériaux ones
HT-66/05/002/A
0
5
10
15
20
25
0
0.5
1
1.5
2
VARIATION OF B2DT
- Local Law of the connection -
Bd2 = 0.7
Bd2 = 0.8
Bd2 = 0.9
Bd2 = 1.0
Bd2 = 1.5
S
X
Y (
M
AP
)
-
contr
has
I
N
T
E
D
E
C
I
its
I
L
lem
E
NT
T
With
O
-
defo EXY
Appear 5.2.6-a: Comparison of
T
B
D
2
: damage and rupture of the connection
5.3
Parameters of damage on the normal direction
5.3.1 Limit of deformation
1N
or threshold of great displacements
In a way similar to the elastic behavior in the tangential direction, it is considered that
decoherence must be initiated at the time of the going beyond of a certain threshold of deformation. We propose
to adopt a value between 10
- 4
and 10
- 3
.
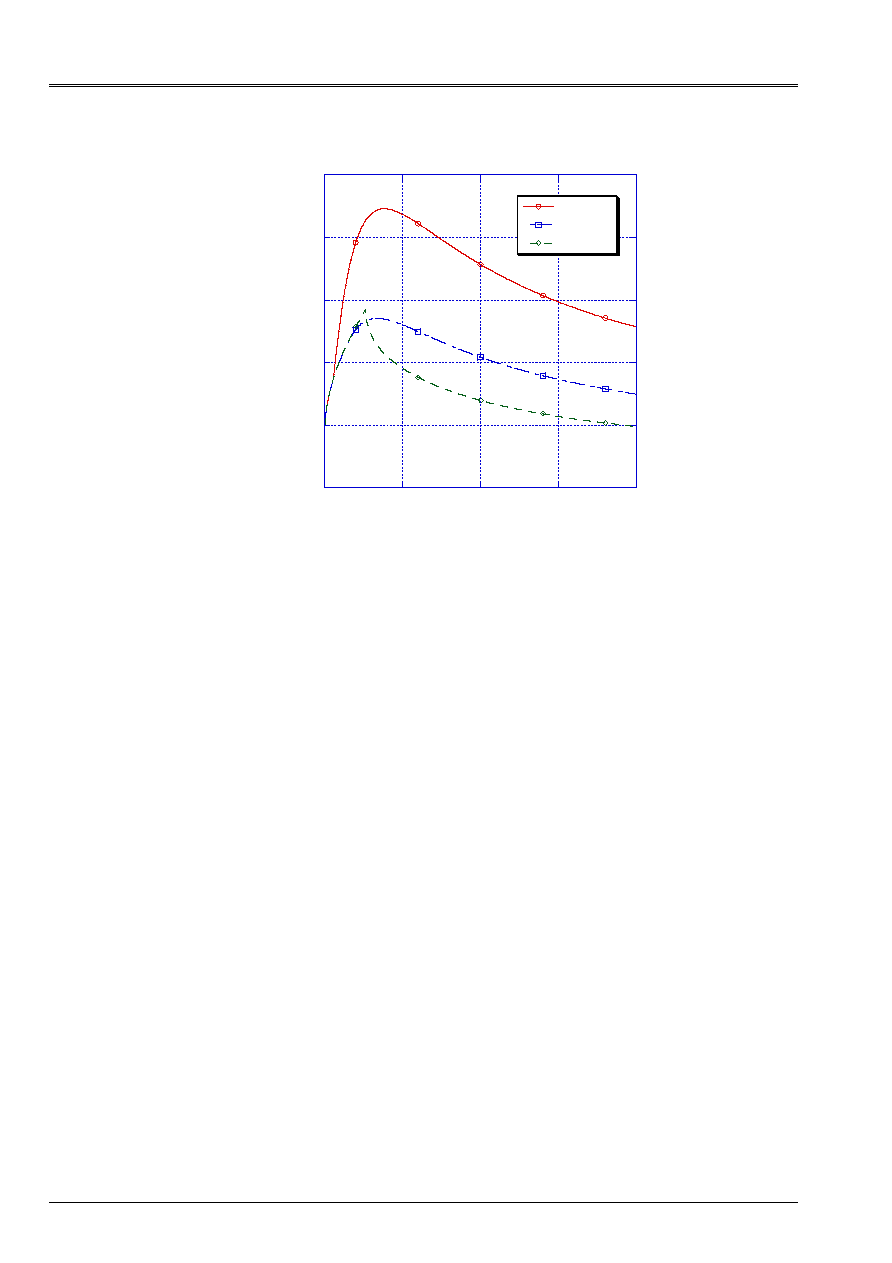
5.3.2 The parameter of damage A
DNN
This parameter controls primarily the slope of degradation of the normal stress compared to
deformation due to the opening of the interface. We propose to use a minimal value of 1x10
- 1
MPa
- 1
, which corresponds to a degradation similar to that of the concrete. Nevertheless, if one wishes to have
a behavior of the connection even more fragile, it is enough to increase this value.
5.3.3 The parameter of damage B
DNN
In combination with the preceding parameter, this parameter controls the damage of the connection,
in particular shape of the curve of behavior in phase post-peak.
We propose to use a value equalizes to 1, or 1,2 for more marked curves.
Code_Aster
®
Version
7.4
Titrate:
Law of behavior (in 2D) for the steel-concrete connection: JOINT_BA
Date:
09/09/05
Author (S):
S. MICHEL-PONNELLE, NR. DOMINGUEZ
Key
:
R7.01.21-A
Page
:
22/26
Manual of Reference
R7.01 booklet: Modelings for the Civil Engineering and the géomatériaux ones
HT-66/05/002/A
0
5
10
15
20
25
0
0.5
1
1.5
2
ADN = 1e-3
ADN = 1e-2
ADN = 1e-1
SY
Y (
M
P
has
)
- C
O
N
T
R
have
NT
E NR
O
rmal
E
of
has
D
H
E
R
E
NCE
-
Normal deformation
Be reproduced 5.3.3-a: behavior of the connection on the normal direction at the time of the opening
interface (normal traction on the connection).
5.4
Parameters of friction
5.4.1 The parameter material
of friction of the fissures
One of the assets of the model suggested here is that it is able to take into account the effects of
friction of the fissures, which, in the case of monotonous loading, appears by a contribution
positive with the shear strength of the connection; in addition, in the cases of loadings
cyclic, it is obvious that the pace of the loops of hysteresis depends directly on the choice of the value
this parameter material. However, the corresponding values were not gauged, since
we did not simulate tests with cyclic loadings yet to validate them.
Temporarily, one proposes to use values lower than 10 MPa, with a maximum value of
equal to 1.0 MPa
- 1
.
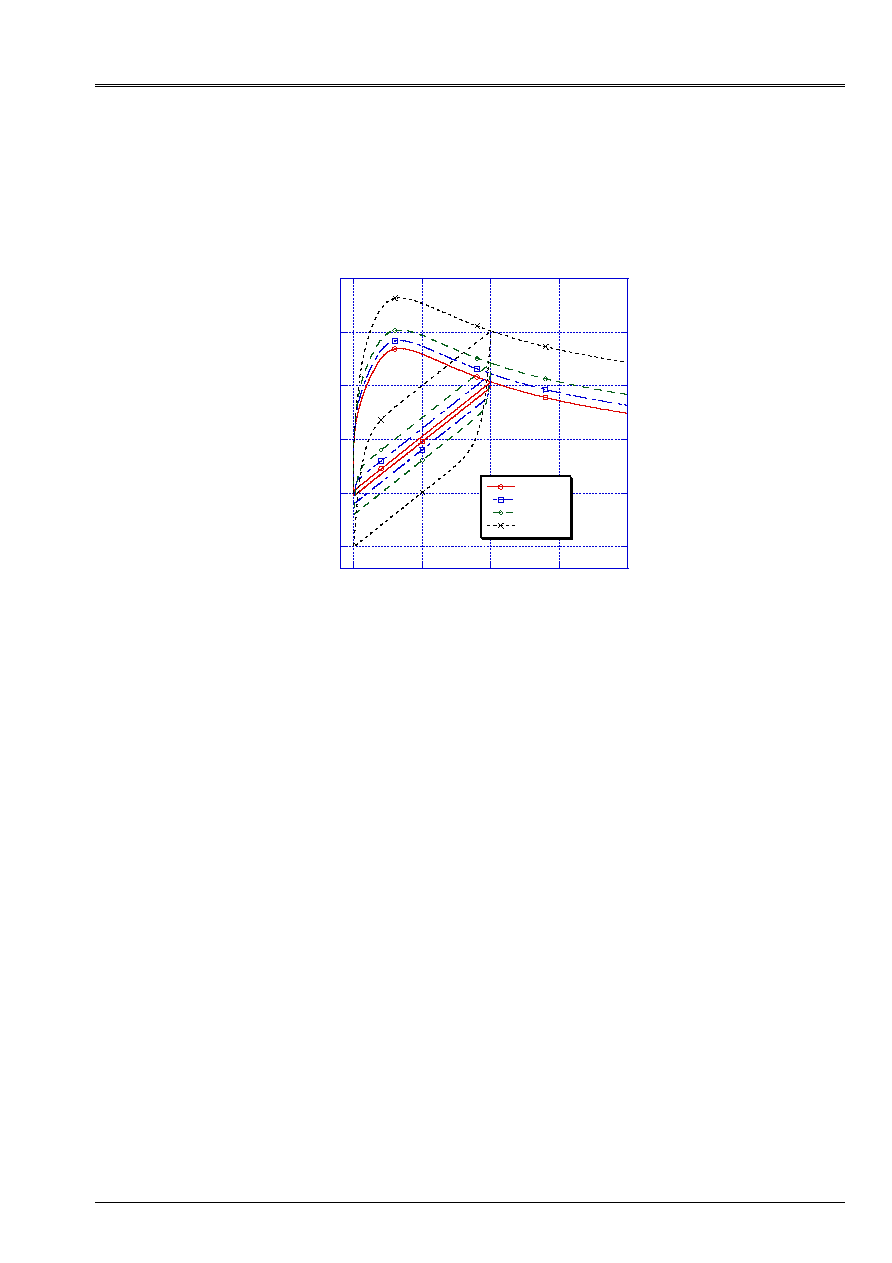
5.4.2 The parameter material
of kinematic work hardening
On [Figure 5.4.2-a], one can appreciate that the reduction in the value of
increase dissipation
hysteretic, but also the resistance of shearing and the residual deformation pseudo-plastic.
That is very important for the cyclic modeling of the connection since in reality, when one
exceed the peak of maximum resistance, one notices that at the time of the discharge there is no more
elastic contribution of the slip, i.e. the residual deformation pseudo-plastic
corresponds exactly to the total slip reached. In other words, once connected all them
fissures in the potential of rupture, longitudinal and tangential layer with the steel bar, the single one
resistance which will prevent the displacement of the reinforcement is the friction resistance of the connection,
produced by the contact and the tangle of the asperities between surfaces concrete concrete.
Code_Aster
®
Version
7.4
Titrate:
Law of behavior (in 2D) for the steel-concrete connection: JOINT_BA
Date:
09/09/05
Author (S):
S. MICHEL-PONNELLE, NR. DOMINGUEZ
Key
:
R7.01.21-A
Page
:
23/26
Manual of Reference
R7.01 booklet: Modelings for the Civil Engineering and the géomatériaux ones
HT-66/05/002/A
As previously, our experiment is limited: one proposes to use a maximum value of
0.1 MPa
- 1
who gives correct results for applications in monotonous loading, and who
seem suitable for cyclic loadings.
- 5
0
5
10
15
20
0
0.5
1
1.5
2
EFFECT OF
has
ON THE LOOPS OF HYSTERESIS
- Friction of the fissures -
100 A 4
100 A 1
100 A .5
100 A .2
S
X
Y (M
AP
)
-
Co
ntr
has
I
N
T
E
of
C
I
its
I
L
L
E
m
E
NT
T
With
O
-
defo EXY
Appear 5.4.2-a: Comparison of
has
: effects on the loops of hysteresis into cyclic
5.4.3 The parameter of influence of containment C
In our model, the influence of containment was taken into account thanks to the application of it
parameter which controls these effects on the connection, and which appears by an increase in
maximum shear stress like by the increase in maximum displacement to the peak
when containment increases.
For the calibration, we carried out simulations with containments of 0, 5, 10 and 15 MPa,
by always using a value of 1.0 for this parameter. It was noticed that if one wants to produce one
kinematic translation of the slip caused by containment, it is enough D `to adopt a value of 1.2
or 1.5 (adimensional). Optionally, it is advised to maintain the value of 1.0 for
ordinary calculations.
5.5
Summary of the parameters
To facilitate the use of the law, the suiant table presents a synthesis of the whole of
parameters of the model of behavior.
It is reminded the meeting that the values or the expressions suggested have only one indicative value, and that
arbitrary combination can give inaccurate and unexpected results compared to the behavior
hoped for connection; in other words, a bad choice of the parameters can produce a strong rigidity
or a weak response of the interface steel concrete.
Code_Aster
®
Version
7.4
Titrate:
Law of behavior (in 2D) for the steel-concrete connection: JOINT_BA
Date:
09/09/05
Author (S):
S. MICHEL-PONNELLE, NR. DOMINGUEZ
Key
:
R7.01.21-A
Page
:
24/26
Manual of Reference
R7.01 booklet: Modelings for the Civil Engineering and the géomatériaux ones
HT-66/05/002/A
Parameter Unit
Value
proposed
Analytical expression
Variables
concerned
D
B
Diameter of
the bar
PEN
H
mm -
Sr
B
PEN
D
H
=
Sr
Relative surface
ribs
C
ARM
Coefficient of
correction by
reinforcements
bound
G
MPa -
concrete
ARM
bound
G
C
G
=
G
concrete
Modulate
rigidity of
concrete
1
T
-
min 1.0x10
- 4
max 1.5x10
- 3
f' C,
Resistance to
compression
concrete
(MPa)
E
has
Modulate
of elasticity of
steel
T
1
With
D
-
min 1.0
max 5.0
(
)
B
has
SR
T
1
C
F
With
E
E
D
+
=
30
'
1
1
E
B
Modulate
of elasticity of
concrete
T
B
D
1
-
min 0.1
max 0.5
2
T
- -
()
(
)
(
)
1.0
9
1
1
4
4
2
+
-
=
T
1
T
1
PEN
2
T
With
With
H
D
D
T
With
D
2
MPa
- 1
min 1.0x10
- 4
max 9.x10
- 2
T
B
D
2
-
min 0.8
max 1.5
MPa
max 10.0
has
MPa
- 1
min 0.01
max 1.0
C
- 1.0
(value
recommended)
1
NR
-
min 10
- 4
max 0.9 10
- 3
NR
With
D
MPa
- 1
min 1.0x10
- 1
(value recommended, not gauged)
NR
B
D
- 1.
(value recommended, not gauged)
Code_Aster
®
Version
7.4
Titrate:
Law of behavior (in 2D) for the steel-concrete connection: JOINT_BA
Date:
09/09/05
Author (S):
S. MICHEL-PONNELLE, NR. DOMINGUEZ
Key
:
R7.01.21-A
Page
:
25/26
Manual of Reference
R7.01 booklet: Modelings for the Civil Engineering and the géomatériaux ones
HT-66/05/002/A
6 Bibliography
[1]
ARMSTRONG, P.J. & FREDERICK, C.O. : In Multiaxial Mathematical Representation off the
Bauschinger Effect. G.E.G.B. ; Carryforward RD/B/NR, 731, 1966.
[2]
BERTERO V.V.: Concrete Seismic behavior off structural linear elements (beams and
columns) and to their connections. Euro-International committee of Concrete (CEB); Bulletin
of information No 131; Paris, France, 1979.
[3]
ELIGEHAUSEN R., POPOV E.P. & BERTERO V.V.: Room jump stress-slipway relationships off
deformed bars under generalized excitations. University off California; Carryforward No.
UCB/EERC-83/23 off the the National Science Foundation, 1983.
[4]
ORTIZ Mr. & SIMO J.C. : Year analysis off has new class off integration algorithms for elastoplastic
constitutive relations. International Newspaper for Numerical Methods in Engineering; Vol. 23,
pp. 353 366, 1986.

Code_Aster
®
Version
7.4
Titrate:
Law of behavior (in 2D) for the steel-concrete connection: JOINT_BA
Date:
09/09/05
Author (S):
S. MICHEL-PONNELLE, NR. DOMINGUEZ
Key
:
R7.01.21-A
Page
:
26/26
Manual of Reference
R7.01 booklet: Modelings for the Civil Engineering and the géomatériaux ones
HT-66/05/002/A
Intentionally white left page.

























