|
Let us now derive the momentum equation resulting from the
Reynolds Transport theorem, Eqn. 3.27. Now we have
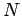 = =
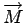 where where
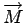 is the
momentum. Note that momentum is a vector quantity and that it has
a component in every coordinate direction. Thus, is the
momentum. Note that momentum is a vector quantity and that it has
a component in every coordinate direction. Thus,
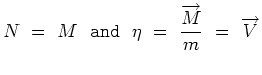 |
(3.39) |
Consider the left hand side of Eqn. 3.27. We have
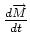 which is proportional to the
applied force as per Newton's Second Law of motion. Thus, which is proportional to the
applied force as per Newton's Second Law of motion. Thus,
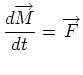 |
(3.40) |
where
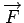 is again a vector. It is necessary to
include both body forces, is again a vector. It is necessary to
include both body forces,
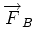 and surface
forces, and surface
forces,
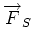 . Thus, . Thus,
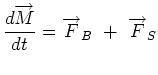 |
(3.41) |
Now we substitute for 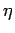 in the right hand side of Eqn.
3.27 giving, in the right hand side of Eqn.
3.27 giving,
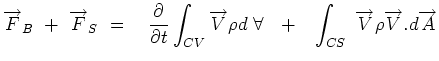 |
(3.42) |
Writing this as three equations, one for each coordinate direction
we have,
The term
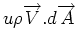 represents the u momentum that is convected in/out by the surface
represents the u momentum that is convected in/out by the surface
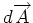 in a direction normal to it. In fact
momentum in other direction can also be convected out from the
same area. These are given by in a direction normal to it. In fact
momentum in other direction can also be convected out from the
same area. These are given by
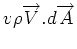 and and
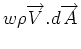 . .
As stated before the term
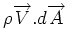 is replaced by is replaced by
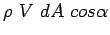 . .
The equation thus derived finds immense application in fluid
dynamic calculations such as force at the bending of a pipe,
thrust developed at the foundation of a rocket nozzle, drag about
an immersed body etc. We consider some of these later.
(c) Aerospace, Mechanical & Mechatronic Engg. 2005
University of Sydney
| 
