|
We know very well that all matter is made up of molecules, which
are in random motion. Any fluid we consider has molecules
bombarding each other and the boundaries, i.e. the walls of the
container. There is no guarantee whatever that molecules are
present at that point at a given instant of time. But still we
say that fluid velocity at a point is so many meters per second or
that density is so many kgs per square meter. Where is the
justification for this? Of course, we can say that we define
density or velocity at point in an average sense. That is as an
average of velocities (or densities) of the molecules that pass
through a small volume surrounding that point. The size of this
small volume has to meet with certain criteria. It must be smaller
than the physical dimensions of the region under consideration
like the wing of an aircraft or the pipe in a hydraulic system. At
the same time it must be sufficiently large to accommodate a large
number of molecules to make any averaging meaningful. It seems
that there is a lower limit to the size of this volume.
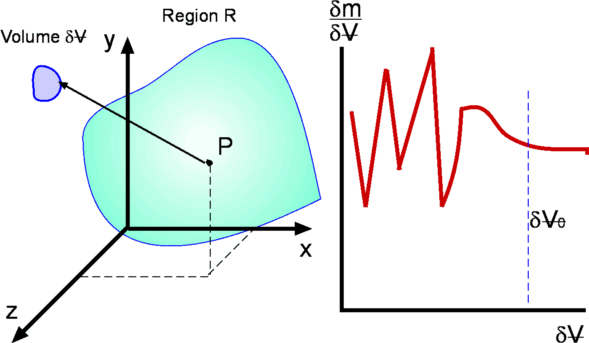
Figure 1.3: Definition of Density |
The existence of this limit is established by considering the
definition of density as mass per unit volume (
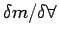 ). Consider a small volume ). Consider a small volume
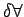 around the
point P (Fig. 1.3) within the region of interest,
R. Let us calculate density at P by considering different
sizes of around the
point P (Fig. 1.3) within the region of interest,
R. Let us calculate density at P by considering different
sizes of
 . Values of density so calculated are
plotted in the same figure. It is clear that the size . Values of density so calculated are
plotted in the same figure. It is clear that the size
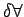 has an enormous influence on the calculated value of
density. Too small a has an enormous influence on the calculated value of
density. Too small a
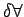 , the value of calculated
density fluctuates because the number of molecules within , the value of calculated
density fluctuates because the number of molecules within
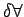 is varying significantly with time. Too big a is varying significantly with time. Too big a
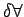 might mean that density itself is varying significantly
within the region of interest. As seemed before it is clear that
there is a limit might mean that density itself is varying significantly
within the region of interest. As seemed before it is clear that
there is a limit
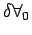 below which molecular
variations assume importance and above which one finds a
macroscopic variation of density within the region. Therefore it
appears that density is best defined as a limit - below which molecular
variations assume importance and above which one finds a
macroscopic variation of density within the region. Therefore it
appears that density is best defined as a limit -
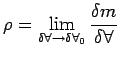 |
(1.1) |
At Standard Temperature and Pressure conditions (STP) the limit
(
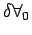 )is around )is around 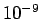 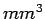 and air at this
tiny volume has about and air at this
tiny volume has about 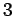 x x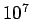 number of molecules. This is a
large enough number to give a constant value of density despite
the rigorous molecular motion within it. For many of the
applications in Fluid Mechanics, this volume is smaller than the
overall dimensions of the regions of interest considered such as
an aeroplane, wing of an aeroplane, ship or the parts of an engine
etc. These considerations do not hold good when we go to greater
altitudes. For example, at an altitude of 130 km the molecular
mean free path is about 10.2 m and there are only number of molecules. This is a
large enough number to give a constant value of density despite
the rigorous molecular motion within it. For many of the
applications in Fluid Mechanics, this volume is smaller than the
overall dimensions of the regions of interest considered such as
an aeroplane, wing of an aeroplane, ship or the parts of an engine
etc. These considerations do not hold good when we go to greater
altitudes. For example, at an altitude of 130 km the molecular
mean free path is about 10.2 m and there are only 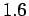 x x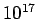 molecules in a cubic meter of air(Molecular Mean Path,
molecules in a cubic meter of air(Molecular Mean Path, 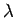 is defined as the average distance a molecule has to travel before
it collides with another molecule. At STP conditions its value is
is defined as the average distance a molecule has to travel before
it collides with another molecule. At STP conditions its value is
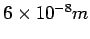 ). Under these conditions it becomes necessary
to consider the effect of every molecule or groups of molecules,
as in calculations concerning re-entry vehicles. That branch of
fluid mechanics is called Rarefied
Gasdynamics. ). Under these conditions it becomes necessary
to consider the effect of every molecule or groups of molecules,
as in calculations concerning re-entry vehicles. That branch of
fluid mechanics is called Rarefied
Gasdynamics.
(c) Aerospace, Mechanical & Mechatronic Engg. 2005
University of Sydney
|

