|
We all have a feel for viscosity. More viscous a fluid more
difficult for it to flow. Oils flow at a slower rate than water.
We understand viscosity as a property that tends to retard fluid
motion.But we do have a more rigorous definition of viscosity,
which can be developed from the thought experiment described
before.
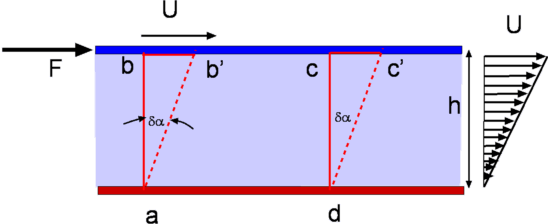
Figure 1.4: Flow between parallel plates |
It was seen that when a shear force is applied to the
top plate the fluid undergoes a continuous deformation
( What is a Fluid? Fig.1.4). As a result the block of fluid
abcd deforms to ab'c'd after a time 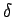 t. Let
the speed of the top plate be U. It is an important property of
fluids that the layer of fluid adjacent to a solid surface moves
with the same velocity as the solid surface. This is called the
"No Slip" condition. Accordingly fluid layer closer to the top
plate moves with a speed U while that closer to the lower plate is
at rest. Thus the velocity of the fluid varies continuously from
zero on the lower plate to U at the upper plate. In other words a
velocity gradient develops in the fluid. In the simple case of the
flow between parallel plates this is a linear profile. The
velocity gradient is given by t. Let
the speed of the top plate be U. It is an important property of
fluids that the layer of fluid adjacent to a solid surface moves
with the same velocity as the solid surface. This is called the
"No Slip" condition. Accordingly fluid layer closer to the top
plate moves with a speed U while that closer to the lower plate is
at rest. Thus the velocity of the fluid varies continuously from
zero on the lower plate to U at the upper plate. In other words a
velocity gradient develops in the fluid. In the simple case of the
flow between parallel plates this is a linear profile. The
velocity gradient is given by
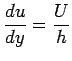 |
(1.2) |
where h is the distance between the two plates.
In a small instant of time 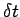 we find that the upper plate
has moved by a distance bb' which is equal to we find that the upper plate
has moved by a distance bb' which is equal to
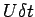 . .
Now
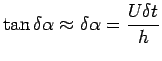 |
(1.3) |
Noting that for solids the shear stress 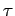 is
proportional to
strain is
proportional to
strain
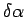 while for fluids it is
proportional to rate
of strain, while for fluids it is
proportional to rate
of strain,
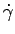 , which in turn is defined as , which in turn is defined as
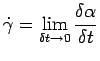 |
(1.4) |
.
Substituting for
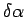 we have we have
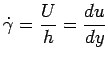 |
(1.5) |
Since 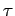 is proportional to is proportional to
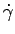 , we
have
or , we
have
or
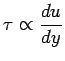 |
(1.6) |
It is found that for common fluids such as air, water
and oil the
relationship between shear stress and velocity
gradient can be
expressed as,
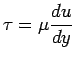 |
(1.7) |
The constant of proportionality 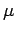 is an important property of
fluids in determining the flow behaviour and is called
Dynamic Viscosity or Absolute
Viscosity. It is usual to refer to it as just
Viscosity. It has the dimensions is an important property of
fluids in determining the flow behaviour and is called
Dynamic Viscosity or Absolute
Viscosity. It is usual to refer to it as just
Viscosity. It has the dimensions 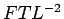 and
units of and
units of 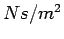 in the SI system. in the SI system.
Fluids for which the shear stress varies linearly as rate of
strain are called Newtonian Fluids. Many of the common
fluids belong to this category- air, water. When the relationship
between shear stress and rate of strain is not linear, the fluid
is designated Non-Newtonian. Examples of this
category are some of the industrial fluids such as plastics,
sludge and biological fluids such as blood. Typical plots of shear
stress vs rate of strain are shown in Fig.1.5. Rheology
is the branch of fluid mechanics which specialises in these
fluids. We consider primarily common fluids such as water and air
and hence restrict ourselves to Newtonian fluids.
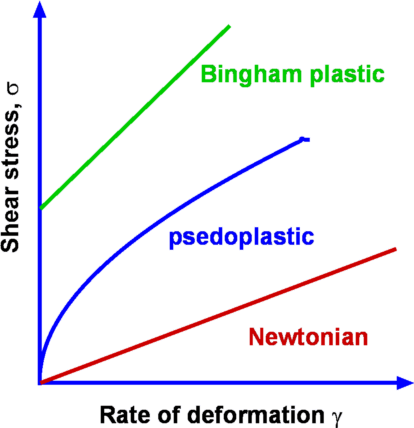
| Figure 1.5 : Flow between parallel plates |
Viscosity of a fluid is strongly dependent on temperature and is a
weak function of pressure. For example, when the pressure of air
is increased from 1 atm to 50 atm, its viscosity increases only by
about 10 percent allowing one to ignore its dependence on
pressure. Fig.1.6 shows the manner of dependence of
viscosity on temperature for some of the common fluids. It is seen
that the viscosity of liquids deceases with temperature while that
for the gases increases with temperature. This difference in
behaviour is explained by the cohesive and intermolecular forces
within the fluid. Liquids are characterized by strong cohesive
forces and close packing of molecules. When temperature increases
cohesive forces are weakened and there is less resistance to
motion. Hence viscosity decreases. With gases, the cohesive forces
are very weak and the molecules are spaced apart. Viscosity is due
to the exchange of momentum between molecules as a result of
random motion. As the temperature increases the molecular activity
increases giving rise to an increased resistance to motion or in
other words viscosity increases.
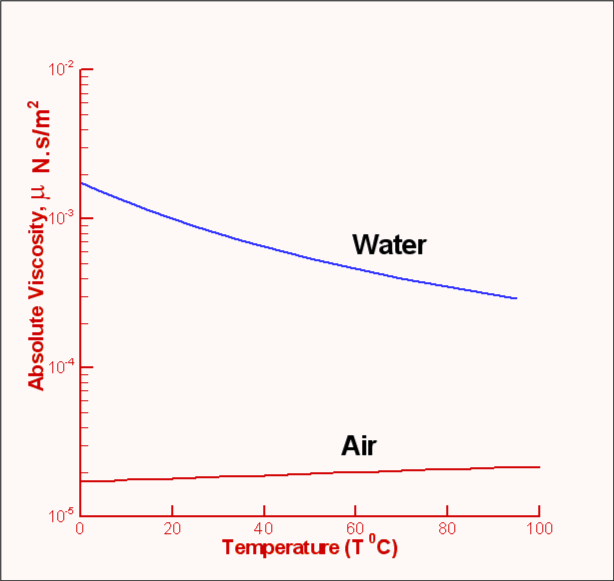
| Figure 1.6 : Viscosity of Air and Water plotted against temperature |
Subsections
(c) Aerospace, Mechanical & Mechatronic Engg. 2005
University of Sydney
| 
