Equation for Pressure Field

We have shown that for a fluid at rest pressure at any point is invariant with direction. But it does not prevent pressure itself varying from point to point within the fluid. In this section we try to establish a relationship for this variation of pressure.

Figure 2.3: Pressure at a point

 

Consider a rectangular element of fluid of dimensions dx x dy x dz with its centre at the point P(x,y,z) as shown in Figure 2.3. Let the pressure acting at the point P be equal to p. It is usually assumed that pressure varies continuously across the element. Consequently the pressures at the different faces of the element are calculated by expanding pressure in a Taylor series about the point P. Second and higher order terms are neglected. Accordingly,

$$PL= p- {\partial p \over \partial x}{dx \over 2},~~ PR= p+ {\partial p \over \partial x}{dx \over 2}$$

$$PG= p- {\partial p \over \partial y}{dy \over 2},~~ PF= p+ {\partial p \over \partial y}{dy \over 2}$$

$$PB= p- {\partial p \over \partial z}{dz \over 2},~~ PT= p+ {\partial p \over \partial z}{dz \over 2}$$

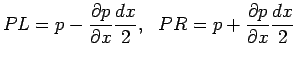
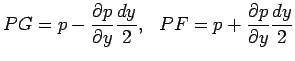
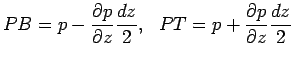
A surface force balance in the x- direction gives

$$\delta F_x = PL-PR = \left( p- {\partial p \over \partial x}{dx \over 2} \right)dy~dz - \left( p+ {\partial p \over \partial x}{dx \over 2} \right)dy~dz~ =-{\partial p \over \partial x}~dx~dy~dz$$ (2.5)

Similar force balancing is carried out in each of the other directions. Upon collecting terms we have for surface forces acting on the fluid element,

$$\delta F_s =- \left( \hat{i}{\partial p \over \partial x} + \hat... ...ial p \over \partial y} +\hat{k}{\partial p \over \partial z} \right)~dx~dy~dz$$ (2.6)

The terms within the parenthesis is called the pressure gradient. i.e.,

$$grad~ p=\nabla p =\left( \hat{i}{\partial p \over \partial x} + ... ...at{j}{\partial \over \partial y} +\hat{k}{\partial \over \partial z} \right)~p$$ (2.7)

Thus,

$$dF_S=-\texttt{grad}~ p~dx~dy~dz=-\nabla p~dx~dy~dz$$ (2.8)

Thus it is seen that the net surface force upon the element is given by the pressure gradient and is not dependent upon the pressure level itself.

(c) Aerospace, Mechanical & Mechatronic Engg. 2005
University of Sydney