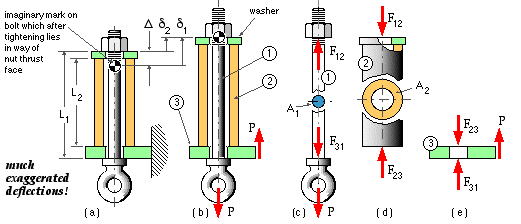
An eyebolt 1 and tubular sleeve 2 are supported by the plate 3 as in (a), (b) below.
Initially the nut is just finger tight ( 'snubbed' - there are no gaps in, and no appreciable loads on the assembly).
Subsequently the nut is tightened by screwing it a known distance Δ along the thread, then the temperature of the sleeve only is increased by t, and finally the load P is suspended from the eye.
Given the axial stiffnesses k₁ and k₂, resolve the indeterminacy in the final loaded state. The washer and support plate 3 are thin - ie. very short axially compared to the bolt and sleeve - and therefore relatively rigid since k is proportional to 1/L. It follows that the only deformations of significance are those of the bolt 1 and sleeve 2.
The sequence of load application (heat, tightening, external load) is irrelevant in this elastic analysis - what matters is the final loaded state after all three have been applied. The significant deformations (δ₁, δ₂) in this final loaded state are assumed to be as shown in (b) in which deformations are grossly exaggerated in order to clarify compatibility constraints. Other deformation assumptions may be equally valid - the result should not be affected by the assumption provided any subsequent analysis is consistent with the assumption. More of this anon.
Emphasising this point once more -

• In figure (a) all components are completely free, ie. unloaded
• In figure (b) loading is complete - initial tightening, heating, and application of external load, P, have all been applied.

Compatibility

By the assumptions of sketch (b) :
δ₁ represents the unknown extension of the (great majority of the) eyebolt 1
δ₂ represents the unknown extension of the cylindrical sleeve 2, and
Δ is the known nut movement along the thread.
For the components to remain in contact - ie. for compatibility - the geometry of (a) and (b) requires that :-

( i)      δ₁ - δ₂  =   Δ

Equilibrium

Before the components are examined individually, all externals on the assembly must be known. The given external load P applied to the eye is supported by the plate 3, hence a known upward load P appears on the free body (b) of the assembly. The support must also exert a bending moment on the plate to equilibrate the P-couple, but this is neglected here as having no bearing on resolution of the indeterminacy - eg. if the cantilevered plate 3 droops then the other components undergo rigid body motion which does not affect the relative motion between 1 and 2.

Free bodies of the separate components are now prepared - (c), (d), (e) - in which the unknown action/reaction at each contact is identified conveniently by the indices of the two components in contact. No components are stuck together so the action/reactions must be 'pushes' on the contacting components - hence F₁₂ is shown in free body (c) pushing on component 1, and on free body (d) pushing on component 2. This force is the resultant of (presumably uniform) pressure over the annular contact area - the washer's purpose is to distribute this pressure evenly.
There are three contacts 1-2, 2-3, 3-1 between the three components, hence the three contact resultants F₁₂, F₂₃, F₃₁ appear on the three free bodies. Equilibrium of all three free bodies requires that :-

( ii)       F₁₂ -  F₃₁   =   P
( iii)     F₁₂ = F₂₃

It is noted particularly from the free bodies (c), (d) that :

• F₁₂ (or P + F₃₁ from ( ii)) represents the unknown tension in the (great majority of the) eyebolt 1
• F₁₂ (or F₂₃ from ( iii)) represents the unknown compression of the tubular sleeve 2

If it is not clear from free body (c) that the eyebolt is tensioned by F₁₂ and not by F₃₁, then the flow analogy should be applied or free bodies drawn cutting the shank of (c) and embracing either end of the bolt.
 

Constitutive Laws

Equation ( 2a) is applied to each deformable component, ensuring that the signs in the constitutive equations tally with the senses of loads and deformations used in the previous two steps.

Eyebolt 1       From above, the eyebolt is subjected to a tensile load F₁₂ and suffers a tensile deformation δ₁, so the constitutive law ( 2a) consistent with compatibility, equilibrium and constant temperature is :-

( iv)     δ₁   =   F₁₂ / k₁       ;       k₁ = ( A E / L )₁

Sleeve 2       From above, the sleeve is subjected to a compressive load F₁₂ and a temperature rise t, and suffers a tensile deformation δ₂, so by inspection or by adhering to a positive tensile convention, the form of ( 2a) consistent with compatibility, equilibrium and temperature rise of this component is :-

( v)       δ₂   =   - F₁₂ / k₂ +   L₂α₂t       ;       k₂ = ( A E / L )₂

Solution

Resolving the indeterminacy by solving the five equations for the three unknown forces and two unknown deformations gives :-

( vi)     F₁₂   =   F_o     where the known initial load is defined as   F_o   =   k_e ( Δ +   L₂α₂t )
in which the equivalent series stiffness k_e is given by 1/k_e = 1/k₁ + 1/k₂
F_o is called the initial load because it is due to nut tightening and heating before the external load P is applied.

This result seems ridiculous since it has F₁₂ (the only failure agent in both 1 and 2) completely independent of the applied load P - ie. the load may be raised out-of-hand with no adverse effects on bolt or sleeve !!!

The channel for the flow analogy is shown at (f) here; the restrictive annular areas are arrowed. 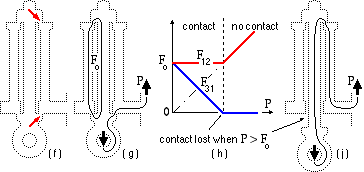Two distinct force paths are suggested in (g) - that of P from the eye directly into the support and byepassing the bolt shank and sleeve, and that of the self-equilibrating initial load F_o in the bolt shank and sleeve. These make physical sense as no external support is necessary to cater for a temperature rise of the sleeve or for a tightening of the nut - these effects, embodied in F_o, are resisted internally in the assemblage. Note that the force paths have been greatly simplified here to avoid confusion in the sketch.

The two forces F₁₂ and F₃₁ are graphed against increasing external load P in (h).
F₁₂ is constant at F_o from ( vi) while from ( ii) F₃₁ drops off from this value in proportion to P, until it becomes zero when P reaches a value of F_o. But F₃₁ is the force between eyebolt and support; it cannot be negative (there is no adhesive to enable the eyebolt to pull down on the support). The physical interpretation of F₃₁ reaching zero is that contact between eyebolt and support is lost as indicated by ( j).
This then is the reason for the apparent anomaly in the foregoing analysis. The analysis is perfectly correct - but only within the limitations of its assumption, implicit in the free bodies (c) and (e), that contact between 1 and 3 is maintained and F₃₁ > 0.
This assumption should not be confused with the unrelated deformation assumption of (b).

If it is desired to increase the load P at which contact is lost, then (h) indicates that F_o must be raised, probably by further nut tightening, Δ. After contact is lost (P > F_o) the arrangement is statically determinate and component loads can be found immediately from equilibrium only. Setting F₃₁ = 0 and F₁₂ = P in the free bodies (c), (d) and (e) demonstrates that all components transmit the external load P. This is confirmed physically by the force path ( j).

Having found the force F₁₂ transmitted through the bolt eg. the bolt's safety can be assessed from the tensile design equation ( 1b) applied to the component 1 :
          n₁     =     (AS/P)₁     =     A_c1S₁/F ₁₂     ;               F₁₂     =     maximum( P, F_o)     from (h).