Fracture mechanics problems

1. A large sheet containing a 50 mm long crack fractures when loaded to 500 MPa.
   Determine the fracture load of a similar sheet with a 100 mm crack.     [ 354 MPa ]
    
2. Rocket motor casings may be fabricated from either of two steels :

   (a)	low alloy steel	yield 1.2 GPa	toughness 70 MPa√m,
   (b)	maraging steel	yield 1.8 GPa	toughness 50 MPa√m

   The relevant Code specifies a design stress of yield/1.5.
   Calculate the minimum defect size which will lead to brittle fracture in service for each material, and comment on the result ( this last is important ).     [ 4.9, 1.1 mm ]
    
3. The bar of 100 x 20 mm rectangular cross-section is loaded by a force of 250 kN as shown.
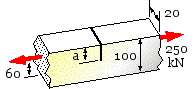
   Determine the critical crack length if the toughness is 50 MPa√m.     [ 14 mm ]
    
4. Derive equation ( 2) by applying the distortion energy failure criterion to the stress components of ( 1).
    
5. The CTS testpiece is from a 1.2 GPa steel.
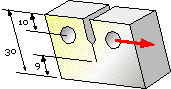
   If the failure load is 10 kN, what fracture toughness is indicated ?
   Is the result valid ?
   Note that width and crack size are reckoned from the load's line of action.     [ 80 MPa√m ]
    
6. The toughness of a 700 MPa yield structural steel is estimated to be 140 MPa√m.
   What size and mass of SEN bend test specimen is necessary, and what capacity of testing machine would be required ?
   Assume fracture at   α = 0.5.     [ 126 kg, 590 kN ]
    
7. The long strip may be made from either of the two materials :

   (a)	tough, weak	yield 700 MPa	plane strain toughness 100 MPa√m
   (b)	brittle, strong	yield 1400 MPa	plane strain toughness 50 MPa√m

   A central crack extends through the strip.
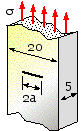
   Plot, as a function of crack length, the failure stress for each material due to the separate mechanisms of elastic fracture and plastic collapse.
   Comment on the trends of these graphs.
    
8. The bar of rectangular cross-section, w x b, is edge-cracked and loaded by a tensile force, N, and a bending moment, M.
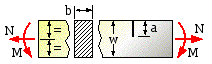
   Consider the equilibrated distribution of yield stress across the ligament and hence show that plastic collapse may be caused by any combination of M and N which satisfies :-
       m + n ( n + 2α ) = ( 1 - α )²         where   α = a/w   ;     n = N/bwS_y   ;     m = 4M/bw² S_y
    
9. A long, 50 mm diameter rod is manufactured from a material of 700 MPa yield and 40 MPa√m toughness. The rod is circumferentially cracked, case ( f), whilst tensioned by a force,   P.
   What is the maximum safe load if the crack depth is 2 mm ?     [ 770 kN ]
   If the load is 200 kN, what crack depth is tolerable ?     [ 12 mm ]
    
10. Welded plates, 10 mm thick, are subjected to bending as shown.
    Crude manufacture leads to the expectation of 2 mm cracks extending right along the weld root. Multiple service failures occur when the deposition properties are as (b) below. Would a change to (a) or to (c) alleviate the problem ?

    deposition	(a)	(b)	(c)
    yield ( MPa )	600	800	1000
    toughness ( MPa√m )	120	90	60

    
    
11. A pressure vessel, of bore 850 mm and wall thickness, w = 24mm, is designed with a safety factor of 2.5 based on the yield of 500MPa. The material's fracture toughness is 50 MPa√m.
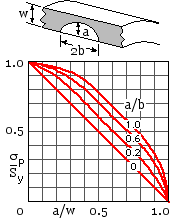
    A semi-elliptical longitudinal fatigue crack ( a=10, b=20 mm) is discovered at the bore during routine inspection. What is the actual safety factor of the flawed vessel.     [ 1.26 ]
    If the toughness were to drop to 35 MPa√m due to a drop in ambient temperature, what then would be the safety factor ?
    Assume configuration factors - plastic as graphed, and elastic 'Y' thus :
          Y = C₁ [ 1 + C₂ ( 1 - cos πα )]     where
          C₁ = 2.24 /( 1 + exp πβ/4)   ;     C₂ = 2.34/( 1 + exp 4√β )   ;     β = a/b
     
12. Derive equation ( 5b) from ( 5a).
     
13. An aluminium shaft, 50 mm diameter and rotating at 3000 rpm, is subjected to a reversed bending moment of 200 Nm. A crack, 0.1 mm deep, extends radially from the surface.
    Estimate the crack depth after 100 hours operation, assuming a Paris exponent of 2.7 and a stress intensity range of 1.6 MPa√m corresponding to a growth rate of 1 mm/Mc. The configuration factor Y may be approximated by that of case ( d).     [ 11 mm ]
     
14. An axially stressed component of width 20 mm is made from a material which obeys the Paris equation with an index of 4 and a crack growth rate of 1 mm/Mc corresponding to a stress intensity range of 6 MPa√m. The configuration factor may be approximated by Y = 0.84/( 1 - α ).
    Neglecting instability, determine the number of cycles necessary for a 5 mm crack to grow to 15 mm, if the component is subjected to a cyclically varying stress of :
    (a) 0 to 40 MPa     [ 2.1 Mc]     ;         (b) 100 to 120 MPa     [ 34 Mc]
     
15. Repeat the previous problem with   K_Ic = 60 MPa√m     [ 2.1, 32 Mc]
     
16. Estimate the life of the component of the previous problem with an initial crack size of 5 mm, if the material yield is 250 MPa. Assume a plastic configuration factor of ( 1 - α ).     [ 2.1, 27 Mc]