PRESSURE VESSELS

• buckling due to external pressure and manufacturing inaccuracies
• the dangerous partnership of low temperatures and welding which always requires special precautions in design and construction.

( i)         S   =   minimum ( S_y /1.6 ,   S_u /4 ,   S_yT /1.5 ,   S_cr /1.6 )

in which S_y and S_u are the tensile yield and ultimate at room temperature, and the last two terms are applicable only at design temperatures above 50^oC, S_yT being the yield strength and S_cr the 100 000 hr creep rupture strength at the design temperature.
Minimum mechanical properties are laid down in AS 1548 Steel Plates for Boilers and Unfired Pressure Vessels, a steel being referenced typically as 'AS1548-2-430-H' in which the '2' refers to Section 2 of AS1548 which deals with a particular type of steel, '430' denotes the minimum ultimate (MPa), and 'H', if it appears, indicates that properties have been verified by high temperature testing rather than being inferred from room temperature properties. Note that properties are slightly thickness- dependent.

Corrosion

Welded Joint Efficiency

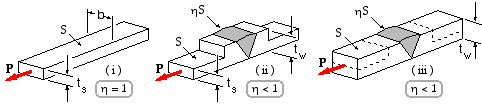
Consider the three bars illustrated below which are all of the same width  b  and material strength  S  and which are loaded by the tensile load  P. The first bar is seamless of thickness  t_s  and the second welded with joint efficiency  η  and thickness  t_w  locally at the joint. The safety factor in this second bar is  Sbt_s / P  away from the joint and  ( η S) bt_w /P  at the joint. If in design these safety factors are to be identical (ie. the bar is not to be weakened by the joint) then  t_w  must equal  t_s /η. However it is most unusual for the economics to justify increase of bar thickness locally in way of the joint - the whole bar must therefore be of thickness  t_w  to cater for an isolated joint inhomogeneity, as shown in the third sketch. The implications of joint efficiency upon cost of raw plate materials are thus readily apparent, however it should be appreciated that away from the joint region the material really needs only to be as thick as a seamless bar.

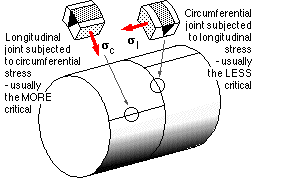
Pressure vessel cylinders are usually made from flat plates which are rolled then welded along longitudinal joints.
On the other hand, circumferential joints are used to attach end closures ( dished ends or heads ) to the cylinder, and to weld together rolled plates for a long vessel if plate size availability or rolling machine capacity are restricted.

Weld types and efficiencies usually differ for longitudinal and circumferential joints, and therefore the joint stresses in a vessel must satisfy both the requirements :-

	longitudinal joint,	efficiency η l ,	circumferential stress	σ c   =   p D / 2t   ≤   η l S
	circumferential joint,	efficiency η c ,	longitudinal stress	σ l   =   p D / 4t   ≤   η c S

In the design context, having selected the material and hence the design stress from ( i), these inequalities may be solved for the plate necessary minimum or calculation thickness, t :-

( 1)         t   =   maximum ( pD/2η _lS ,   pD/4η _cS )

In this formula, AS 1210 takes the diameter to be the mean at the wall mid-surface ( D = D_i + t ) though it quotes the equation conveniently in terms of D_i . As the circumferential stress is twice the longitudinal it follows that the first of these inequalities is usually controlling - provided that η _c is greater than half η _l, which is commonly the case. A plate thickness T, such that ( T - c) ≥ t, would be chosen from a commercially available range such as the BHP plate size schedule, referred to in Problem 3 below.

The Code defines four classes of vessel manufacture - 1, 2 ( A & B ) 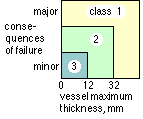and 3 - and provides details of the weld types and efficiencies which are permissible in each class. Some of the major differences between the classes are summarised in the table below; other requirements such as certification of welders' skills need not be gone into here. The sketch indicates that the most expensive Class 1 vessels are mandatory if failure is potentially lethal, no matter what the thickness. Class 2 vessels having a wall thickness greater than 32 mm are inadmissible, and so on. All steel vessels are hydrostatically tested after manufacture to 150% of the design pressure.
 

Class of vessel	1	2A	2B	3
Plate thickness, T mm	no limit	T ≤ 32		T ≤ 12
η l (double butt mandatory)	1.0	0.85	0.75	0.65
η c	- - - depends on weld type, usually less than η l - - -
Heat treatment	required	- - - not required - - -
Radiographic examination	required	spot	- - - not required - - -

A pressure vessel is shown entering a heat treatment furnace - clearly the cost associated with heat treatment is not negligible.

It is apparent that in the design process, the selection of class (if scope for choice exists), and of weld type, involves an economical balance between welding costs ( including inspection and repairing flaws during manufacture, if carried out ) and the cost of plate - a categorical decision cannot be made until the relative or total cost of all potential candidates can be compared.

Welds should preferably not be situated adjacent to anomalies such as stress concentrations or inhomogeneities due to other welds, especially major structural welds. Hence the staggering of the two longitudinal welds in the sketch above.

The two ends of the cylindrical portion of a pressure vessel are usually closed off by dished ends (or heads as they're often called) welded to the cylinder. Heads are available in various shapes and sizes, and we must be able to design them in the same way as we can design the cylindrical components . . . . so let's now look at thin shells of revolution . . . .