|
Force, 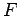 given by Eq. 2.33 is the resultant force acting
on the plane due to the liquid and acts at what is called the
Center of Pressure (CP). It does not act at the centroid of the
plane as it may seem. Let the coordinates of CP be given by Eq. 2.33 is the resultant force acting
on the plane due to the liquid and acts at what is called the
Center of Pressure (CP). It does not act at the centroid of the
plane as it may seem. Let the coordinates of CP be 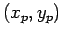 .
Noting that the moment of the resultant force is equal to the
moment of the distributed force about the same axis, we have .
Noting that the moment of the resultant force is equal to the
moment of the distributed force about the same axis, we have
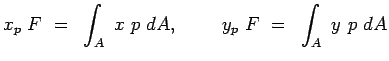 |
(2.34) |
Before substituting for 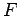 in the above equation we note that the
atmospheric pressure in the above equation we note that the
atmospheric pressure 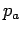 acting at the free surface also acts
everywhere within the fluid and also on both sides of the plane.
As such it does not contribute to the net force upon the plane. So
we drop term acting at the free surface also acts
everywhere within the fluid and also on both sides of the plane.
As such it does not contribute to the net force upon the plane. So
we drop term 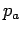 from the equation for from the equation for 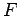 . Eq.2.34 becomes . Eq.2.34 becomes
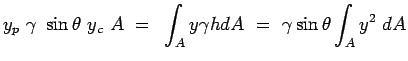 |
(2.35) |
The term
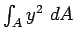 is the well-known second moment of area
about the x-axis denoted by is the well-known second moment of area
about the x-axis denoted by 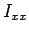 leading to leading to
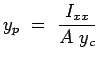 |
(2.36) |
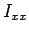 is related to that about the x-axis passing through the centroid of the area, is related to that about the x-axis passing through the centroid of the area,
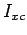 through the Parallel Axes Theorem given by through the Parallel Axes Theorem given by
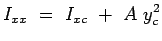 |
(2.37) |
Consequently, we have
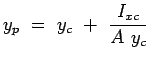 |
(2.38) |
Similarly, taking moments about the y-axis, we obtain,
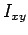 is the product of inertia with respect to x and y axes.
Again on the application of the parallel axis theorem we have is the product of inertia with respect to x and y axes.
Again on the application of the parallel axis theorem we have
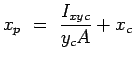 |
(2.40) |
where 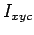 is the product of inertia about the axes passing
through the centroid. The coordinates of the Centre of Pressure
are thus given by is the product of inertia about the axes passing
through the centroid. The coordinates of the Centre of Pressure
are thus given by 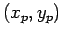 (Eqns. 2.40 and 2.38). (Eqns. 2.40 and 2.38).
The resulting force upon the immersed surface is therefore given
by
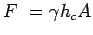 |
(2.41) |
The centre of pressure is given by
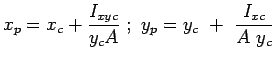 |
(2.42) |
Expressions for the moments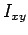 , , 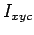 etc for some of the common shapes are given in the next section. etc for some of the common shapes are given in the next section.
(c) Aerospace, Mechanical & Mechatronic Engg. 2005
University of Sydney
| 
