|
The other important utility of the hydrostatic equation
is in the determination of force acting upon
submerged bodies. Among the innumerable applications of this are
the force calculation in storage tanks, ships, dams etc.
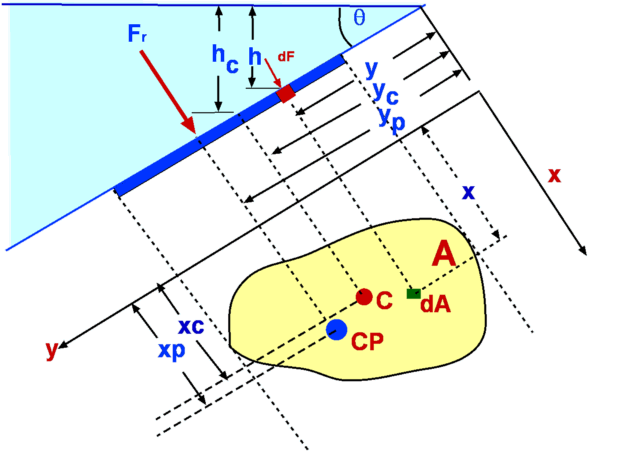
| Figure 2.13 : Force upon a
submerged object |
First consider a planar arbitrary shape submerged in a liquid as
shown in the figure. The plane makes an angle 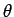 with the liquid surface, which is a free surface. The depth of
water over the plane varies linearly. This configuration is
efficiently handled by prescribing a coordinate frame such that
the y-axis is aligned with the submerged plane. Consider an
infinitesimally small area
with the liquid surface, which is a free surface. The depth of
water over the plane varies linearly. This configuration is
efficiently handled by prescribing a coordinate frame such that
the y-axis is aligned with the submerged plane. Consider an
infinitesimally small area 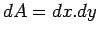 at a (x,y). Let this small
area be located at a depth at a (x,y). Let this small
area be located at a depth 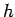 from the free surface. From
Eq.2.18 we know that from the free surface. From
Eq.2.18 we know that
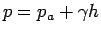 |
(2.30) |
where 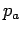 is the pressure acting on the free surface. The
hydrostatic force on the plane is given by, is the pressure acting on the free surface. The
hydrostatic force on the plane is given by,
The integral,
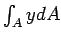 is the first moment of surface area
about x axis. If is the first moment of surface area
about x axis. If 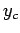 is the y-coordinate of the centroid of the
area we have, is the y-coordinate of the centroid of the
area we have,
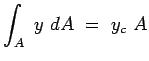 |
(2.32) |
Consequently, Eq. 2.31 is rewritten as
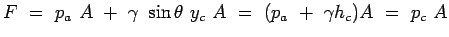 |
(2.33) |
where
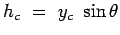 and and 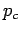 is the pressure acting at
the centroid. is the pressure acting at
the centroid.
Subsections
(c) Aerospace, Mechanical & Mechatronic Engg. 2005
University of Sydney
|

