|
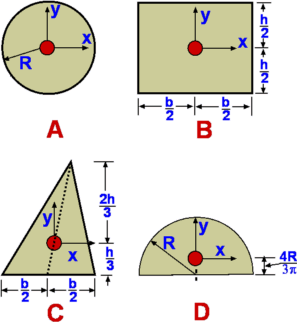
| Figure 2.14 : Properties of some common shapes |
Note that the determination of the resultant force 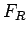 hinges on
the knowledge of the position of the centroid for the given shape.
The location of hinges on
the knowledge of the position of the centroid for the given shape.
The location of 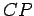 , the Center of Pressure depends upon the
moment of inertia and the product of inertia. These are functions
of the geometry only and can be calculated once the shape is
given. Table 2.2 along with Figure 2.14 gives
these properties for some of the common shapes. , the Center of Pressure depends upon the
moment of inertia and the product of inertia. These are functions
of the geometry only and can be calculated once the shape is
given. Table 2.2 along with Figure 2.14 gives
these properties for some of the common shapes.
(c) Aerospace, Mechanical & Mechatronic Engg. 2005
University of Sydney
|

