Strains

Cylinder strains are of fundamental importance when resolving statically indeterminate assemblages of cylinders such as compound cylinders. Normal strain components are related to normal stress components through the elastic three-dimensional constitutive law. Thus, from ( 3)

( x)        ε_t   =   [ σ_t - ν ( σ_r + σ_a ) ] / E   =   [ ( 1 - ν ) σ_m - νσ_a + ( 1 + ν ) σ_v / γ ] / E
               ε_r   =   [ σ_r - ν ( σ_a + σ_t ) ] / E   =   [ ( 1 - ν ) σ_m - νσ_a -   ( 1 + ν ) σ_v / γ ] / E
                ε_a   =   [ σ_a - ν ( σ_t + σ_r ) ] / E   =   ( σ_a - 2 ν σ_m ) / E       ie. γ-independent as Lamé requires.

If temperature effects occur then α.δT must be added to each strain component.

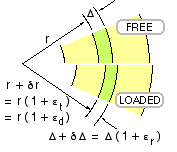
The physical interpretation of ε_r and ε_t is shown in the sketch, in which ε_r = δΔ / Δ is the radial component of strain.
When a cylinder is loaded, we are interested in how it 'breathes' - how its diameter changes as pressures are varied. This is measured by the diametral strain, ε_d. Circumference is always proportional to diameter, therefore circumferential strain (which is just the tangential strain component, ε_t ) is always identical to diametral strain - so from ( x)

( xi)       ε_d   =   δD / D   =   ε_t   =   [ ( 1 - ν ) σ_m - νσ_a + ( 1 + ν ) σ_v / γ ] / E

Note the distinction between the rather confusing terminology here - diametral strain is the strain of a diameter, but radial strain is NOT the strain of a radius, it is merely the component of strain in the radial direction, as noted above.

Autofrettage

Shot-peening, used for establishing a compressive stress in the surface layers of a shaft for example, is generally unsuited to cylinders since the effect is too surface-localised.

Compound cylinders

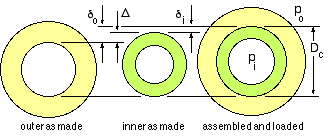
Before safety of either cylinder can be addressed, the common interface pressure p_c must be known. But the problem is statically indeterminate since statics reveals only that if p_c exists as a contact pressure internal to the outer cylinder, then the inner cylinder is pressurised externally by the same amount. Geometric compatibility and the cylinders' constitutive laws ( xi) must be invoked. If the common diameter D_c increases by δ_i measured on the inner cylinder as sketched, and by δ_o measured on the outer, then compatibility requires that :
                Δ   =   δ_o - δ_i
Combination of the equilibrium and constitutive considerations proceeds as follows, in which γ_o, E and ν refer to the appropriate cylinder :-

	INNER	OUTER
internal press.	pi	pc
external press.	pc	po
σm - eq ( 2)	( pi - γo pc ) / ( γo - 1 )	( pc - γo po ) / ( γo - 1 )
σv - eq ( 2)	( pi - pc ) γo / ( γo - 1 )	( pc - po ) γo / ( γo - 1 )
strain at Dc	at γ = γo	at γ = 1
εd - eq ( xi)	[ ( 1 - ν ) σm + ( 1 + ν ) σv / γo ] / E	[ ( 1 - ν ) σm + ( 1 + ν ) σv ] / E
that is	δi/Dc = { 2pi - [(1-ν)γo +1 +ν ] pc } / (γo-1)E	δo/Dc = { [(1+ν)γo +1 -ν ] pc - 2γopo } / (γo-1)E

Inserting these last expressions for δ_i and δ_o into the compatibility equation above, and solving for p_c, leads to the desired result :
Thus, knowing the parameters for each cylinder ( γ_o, E, ν ), the initial interference ( Δ/D_c ) and the loading ( p_i, p_o ), this equation enables solution for the common interface pressure, p_c. Notice how the RHS comprises three loading terms - the first due to the initial interference, the second due to the internal pressure acting inside the inner component, and the third due to the external pressure acting outside the outer component. The static indeterminacy having been resolved by ( 4), the safety of each cylinder may then be examined.

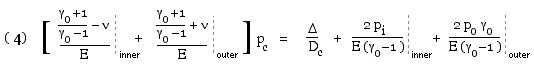
The stresses in a particular compound cylinder are shown, 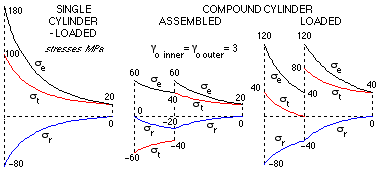after initial assembly and subsequent internal pressurisation. The stresses are significantly lower than those in a single cylinder of the same overall proportions and load. The tangential stress in the inner cylinder is compressive as a result of the as-assembled interference fit, but becomes tensile after the internal pressure is raised to 80 MPa. Quoted equivalent stresses are from the maximum shear stress failure theory.

Note that most texts give an equation for calculating p_c only upon initial assembly not after pressurising - such an equation corresponds to ( 4) with the pressures p_i and p_o set to zero.

One particular application of compound cylinders is when the hub of a gear or coupling is shrunk or force- fitted on to a shaft, with subsequent torque transfer between hub and shaft. Solution of this loading must be carried out numerically (by finite elements for example) however we examine now an approximate model of torsional loading of pressurised cylinders to gain some appreciation of real behaviour.