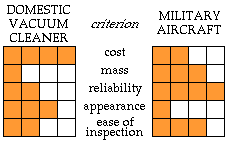
 The sketch illustrates the importance of five criteria common to two different artefacts.
The sketch illustrates the importance of five criteria common to two different artefacts.
At the conclusion of the practicalisation activity, we have a number of candidate solutions which meet all the constraints. These now have to be evaluated - that is compared with one another on the basis of the problem criteria - in order to select the optimum solution.
Evaluation consists of three distinct steps, carried out by the designer :
1. Relative importance of the criteria
Different sets of criteria are associated with different problems. One particular criterion which may be common to different problems usually assumes different significance in these problems.
 The sketch illustrates the importance of five criteria common to two different artefacts.
The sketch illustrates the importance of five criteria common to two different artefacts.
In the design of a domestic vacuum cleaner, cost is probably the most important criterion since potential purchasers' first thought is the effect on their pockets. Undiscerning consumers are not so aware of reliability issues - the importance of the reliability criterion to the designer might therefore be slight, though he has to remember that poor reliability can be expensive to the manufacturer through having to honour statutory guarantees.
The reliability of a military aircraft on the other hand is of prime importance since air-readiness is a vital round-the-clock necessity. The visual aesthetics - the appearancecriterion - of the aircraft is relatively trivial, whereas appearance is important in making a profit from domestic vacuum cleaner sales.
The relative importance of the jth criterion in a problem is termed the weight, wj (or weighting or weight factor) of that criterion. It's the relative, rather than the absolute values of the criteria weights which are significant.
From the sketch for example, wappearance might be 75% for a domestic vacuum cleaner but only 25% for a military aircraft.
Different people often attach different degrees of importance to the same criterion for the same problem - thus the manufacturer of a vacuum cleaner might assign wmass = 25%, whereas the person who has to clean a lot of stairs might assign 90% to this weighting. Again, it's up to the designer to find out the stakeholders involved with the solution, and what their agenda are likely to be. Only then can realistic weights be assigned.
If the weighting for a certain criterion differs markedly between folk then it's probably best to consider the two extremes in further work. A certain candidate may be so much better than the others that a perturbation in one or two weightings may not affect the outcome of the evaluation activity. Conversely if the optimum is sensitive to certain weights then a more rigorous examination is called for.
2. Satisfaction of the criteria - utility
In general the various candidate solutions for a particular problem satisfy the various criteria to various degrees. The degree to which the ith candidate satisfies the jth criterion is characterised by the utility, ui,j - often a real number normalised such that 0 ≤ ui,j ≤ 1 or 100%.
If there are M candidates and N criteria then it is up to the designer to assign the MxN utility values. The utilities must be logical and consistent - it's no good setting u4,9= 50% and u7,9= 25% unless the designer can justify that candidate 4 satisfies criterion 9 approximately twice as well as candidate 7.
It is recommended that when assigning utilities the designer
3. Overall utility
The ith candidate's degree of satisfaction of the jth criterion is the utility ui,j
The ith candidate's degree of satisfaction of the problem as a whole is its overall utility, Ui which in its simplest form is represented by the mean weighted utility : Ui = S wj ui,j /S wj
If utilities are not independent then this simple linear weighting may be inaccurate and call for more complex formulation of the overall utility.
The optimum candidate is that with the highest overall utility, as this reflects a candidate's fitness for the criteria-defined problem.
 EXAMPLE
EXAMPLE
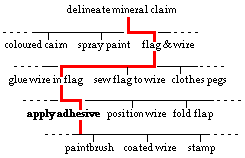
The accepted method of laying claim to new mineral deposits in the bush involves sticking survey markers (or 'pegs') into the ground around the periphery of the claimed area. A marker usually consists of a coloured plastic flag attached to a metal wire mast which is thick enough to permit insertion into the ground without buckling.
Markers are manufactured in their thousands by a sheltered workshop for disabled people who currently cut up rolls of coloured plastic cloth into rectangles, paint PVA adhesive onto an edge of each rectangle with a paint brush, then fold the edge over to secure a pre-cut length of straightened wire as illustrated.
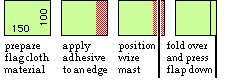
We pick up the story as the workshop re-assesses its operations in an effort to speed up the current manual processes by supplementing them with labour-saving devices. The particular sub-problem of interest is 'How to apply adhesive to the flag?', other problems such as 'How to fold the flag flap?', are not addressed here.
The following candidates for applying adhesive have been proposed and practicalised elsewhere :
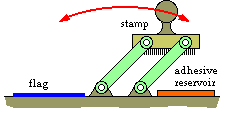
The safety constraint is particularly relevant to handicapped operators.
Criteria relevant to the adhesive application process are :
There is no point in using numerically refined weights here (eg. 47%) because the nature of the problem cannot justify such refinement - integer weights in the range [ 0: 3] will be quite sufficient.
Of the above criteria, operator demands are clearly extremely important in this sensitive application, while robustness is required for trouble-free operation. Weight factors of '3' will be assigned to these criteria. (Although robustness depends to some extent on later detail design, candidates based on small orifices eg. are thought to increase maintenance requirements and this high weighting will militate against these candidates.)
Compatibility with other operations is relatively insignificant as it is not seen to be difficult to marry other operations to adhesive application (unless this is very complicated). The initial cost is not highly weighted either, mainly because all candidates are unsophisticated and cheap. So a weight of '1' will be adopted for both these criteria.
Nothing much separates the remaining criteria so they will be assigned weights of '2'.
The criterion of operator demands will be used to demonstrate brief arguments for the choice of utilities. The candidates are first sorted in order, then the utilities in the range [ 0: 5 ] are assigned (again there is no justification for using numerically more refined values).
Utilities should not be expressed as either 'bad' or 'good' - binary utilities are too coarse. The binary 0/1 is too easily misinterpreted as reject/accept (rather than bad/good) which leads to the incorrect rejection of a candidate whose satisfaction of a single criterion is poor.
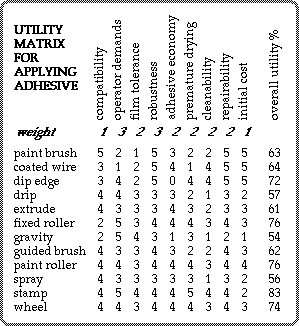 The utilities for the remaining criteria are assigned in a similar manner and result in the utility matrix illustrated. The overall utilities are obtained from the linear weighting formula above, and expressed as percentages of the maximum utility which is '5' here.
The utilities for the remaining criteria are assigned in a similar manner and result in the utility matrix illustrated. The overall utilities are obtained from the linear weighting formula above, and expressed as percentages of the maximum utility which is '5' here.
On the basis of the assigned weights and utilities, the stamp candidate is clearly the optimum, while solutions based upon rollers or wheels are also suitable.
No matter what the scenario - always check your assumptions if you're given half a chance. In the present context it would be advisable to re-assess the utility matrix with amended values of weights and utilities, to see if the problem is sensitive or insensitive to the values assumed. You usually cannot be confident in a one-off result until you have also assessed sensitivity.
The evaluation of utility for a given criterion in more sophisticated problems may be assisted by a utility function which enables the utility to be quickly evaluated in terms of candidate attributes.
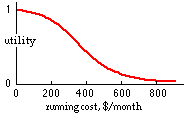 You might set up the utility function illustrated, assigning a utility of 100% to running costs which approached zero, and a utility of effectively zero for costs over $600. The function between these limits would be established only by detailed knowledge of the effect of costs on your personal financial state, and clearly reflects very subjective utilities. Setting up the function is time-consuming, but again there are computer programs to assist in defining the statistically 'best' function.
You might set up the utility function illustrated, assigning a utility of 100% to running costs which approached zero, and a utility of effectively zero for costs over $600. The function between these limits would be established only by detailed knowledge of the effect of costs on your personal financial state, and clearly reflects very subjective utilities. Setting up the function is time-consuming, but again there are computer programs to assist in defining the statistically 'best' function.
Another criterion in new car selection is maneuverabilitywhich depends upon attributes such as turning radius, vehicle length, steering wheel turns lock-to-lock, all round visibility whilst parking, effort necessary to turn steering wheel and so on.
Setting up a utility function for this criterion is obviously very difficult - establishing values of the attributes is easy enough, but ascribing a unique logical utility value to an arbitrary combination of them is not.
Evaluation is like any other activity - the end justifies the means. The effort devoted to evaluation should be in keeping with the importance of the problem. Utility functions are unnecessary for the scope of problem encountered in this course. But whatever the evaluation technique used - basic or sophisticated - the following guidelines must be followed
| Evaluation is a complete waste of time unless all candidates are practical. The most common faults in design include insufficient candidates and inadequate practicalisation, so don't waste effort evaluating at the expense of these activities. |
| Weight factors and utilities must be justifiable (logical & self-consistent) and applied objectively. |
| Constraints and criteria once identified must not be ignored. |
| If you have partially completed an evaluation and you realise that you have omitted a criterion, then you must start evaluation once again with this new criterion incorporated. |
| Evaluation must be based on ALL criteria. Candidates should be trashed on the basis of constraints not of criteria. A very common mistake is to trash on the basis of a single criterion - for example metal A is rejected because it is too heavy, metal B is passed over because it is difficult to obtain . . . and so on. It is easy to kill off all candidates by selecting a single criterion for each - not that one would deliberately set out to do this, but misapplication has just the same effect whether it is inadvertent or deliberate. |
| Another failing is to reject all candidates except one, which by default must then be adopted with inadequate criticism - the solution then depends to a large extent upon the order in which candidates are addressed. This approach can lead to dreadful difficulties later on, when the inherent deficiencies of the poorly assessed 'optimum' become all too apparent. |
| ALL CRITERIA MUST BE APPLIED CONSISTENTLY TO ALL CANDIDATES |
| Guard against making up your mind, perhaps unwittingly, that a particular solution is optimum, then tailoring arguments (again perhaps unwittingly) to bolster this preconception. |
| Do not vacillate when making a decision - your time is precious. |
It may help your appreciation of the evaluation activity if you consider it being carried out on you - one of the candidates who sits an examination in order to answer the problem 'Is this candidate fit to proceed to the next unit ?' You would object strongly if you were barred from proceeding just because of a low utility in one of the criteria - ie. just because you achieved 2/10 for one question in the exam. Evaluation must be based on the overall utility (your mark for the exam as a whole) and not on an individual utility.
The evaluation activity - like many facets of design - seems at first meeting to be a long-winded process. It is at first, if it's to be done well. But like all skills - practice makes perfect, practice makes less onerous, practice makes more interesting.
The optimum solution has now been deduced. It only remains to complete the design by explaining it in a feasibility study