Gear failure - reliability

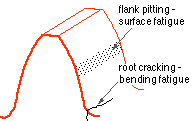
The photoelastic results of contacting gear teeth shown here have important implications for tooth safety :

• high stresses occur where the teeth contact one another;
• bending stresses occur at the root of the lower cantilevered tooth whose fillet radius is large
• much higher bending stresses occur at the root of the upper tooth whose fillet radius is small: this is yet another manifestation of stress concentration in way of geometric singularities.

The following treatment of gear reliability is a gross simplification of the American Gear Manufacturers Association (AGMA) code of practice, AGMA 2001. The treatment aims to demonstrate one approach to fatigue design rather than to transform the reader into a gearing expert.

Apart from one-off overloads, there are three common modes of tooth failure

• bending fatigue leading to root cracking,
• surface contact fatigue leading to flank pitting, and
• lubrication breakdown leading to scuffing.

Since fatigue is prevalent in the other two failure modes, the AGMA employs a reliability approach rather than a safety factor approach in assessing a tooth's tolerance of damage - its bending strength and its pitting resistance. In a reliability analysis, knowledge of a component's load-life (S-N) relationship enables a load to be considered from the point of view of its effect on component life rather than whether it leads to total failure or to total non-failure. A smaller load increases life, a larger load reduces life; whether the safety factor is greater or less than one is irrelevant - indeed the whole concept of safety factor is inappropriate in the context of reliability.

In the succeeding sections therefore, we first determine the effective damaging tooth force   F* due to the power transmitted and the shock / vibration intrinsic to the gears' manufacture and operational environment. The stress,   σ, due to this force is then deduced from bending theory, or from Hertzian contact theory in the case of pitting, and the resulting life follows from the load-life curve appropriate to bending or to contact fatigue as the case may be.
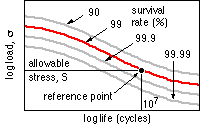
It will be recalled that the load-life diagram for a particular material and given type of loading is generally of the form illustrated, with curves corresponding to different survival rates being approximately parallel to one another - the 99% survival curve eg. implies that one sample in a hundred fails to reach the life given by the curve for a particular load. We shall consider only steel materials (carbon steels induction- or through-hardened, nitrided alloy steels etc). Rather than provide the complete load-life diagram for each steel, the AGMA chooses a reference point on the curve corresponding to 99% survival rate after   10⁷ unidirectional loading cycles, and cites the corresponding allowable stress,   S, as a representative property of the steel. So, for any given load ( σ) the life and survival rate (reliability) may be correlated through :

( 12 )         σ   =   S ∗ life factor ( K_L or C_L ) / reliability factor ( K_R )       where :
 

RELIABILITY FACTOR	% survival	KR
fewer than one failure in 10,000	99.99	1.50
fewer than one failure in 1,000	99.9	1.25
fewer than one failure in 100	99	1.00
fewer than one failure in 10	90	0.85

• The reliability factor, K_R, caters for survival rates other than 99%. Since the survival contours are essentially parallel to one another on a logarithmic scale, then simple multiplying factors enable load correlation, as tabled :-
• The life factor ( K_L for bending, C_L for pitting) caters for lives other than 10⁷ cycles. Since the load-life diagrams for all the steels considered are of the same shape essentially, normalising by the allowable stress will result in a unique K_L (or C_L) -versus- life curve for all steels which will be presented later.

Further explanation of the derivation of ( 12) is presented here.

These aspects when combined will result in gear tooth design equations, one for bending strength and one for pitting resistance, which embrace load (transmitted power), dimensions (primarily size characterised by module), material (allowable stress) and life rather than safety.

Tooth forces

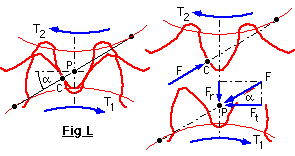
( 13 )         T _i   =   F R_oi   =   F ( R _i cos α )   =   ( F cos α ) R _i   =   F_t R _i   ;       i = 1,2

                                  where   F_t is the useful tangential component of the contact force at the pitch point. The radial component, F_r, is useless and tends only to separate the gears (or pitch cylinders) - note that ( 13) tallies with ( 1) which neglected   F_r.
The pressure angle in Fig L should more correctly be the extended value, and correspondingly ( 13) should really be cast in terms of the actual pitch radius. We neglect such niceties in the present general development.

The steady power transferred, P, is :-

( 14 )           P   =   ω _i T _i   ;       i = 1, 2       the power transfer in rotational terms equals
                            =   ω _i F_t R _i   =   F_t v           the power transfer in translational terms, from ( 1)

Athough the positive drive ensures that there is no speed loss, there will be torque and power losses due to sliding. Spur gear efficiencies exceeding 99% have been reported, however a value of around 96% is more appropriate for run-of-the-mill design - this allows for bearing and aerodynamic losses in addition to tooth friction.

Gear analysis or design usually starts with a known time-averaged (ie. steady) power transfer - these last equations enable the uniform transmitted load   F_t to be found. The corresponding failure-producing (ie. damaging) load   F* will be greater than  F_t because of shock, vibration caused by less-than-perfect tooth profiles and mounting rigidity, and so on. We write :

( 15 )         F*   =   K_a K_v K_m F_t

                            in which the various empirical K-factors, all ≥ 1, each reflects the extra damage caused by a particular, separately identifiable practical non-uniformity, as follows :-

Ka	is an   application factor to allow for the non-uniformity of input and/or output torque inherent in the machinery connected to the gears. Typical values are :- APPLICATION FACTOR   Ka FOR REDUCTION GEARS     ( x 1.1 if speed-up drive ) driving machinery uniform electric motor steam turbine gas turbine light shocks multicylinder combustion engine heavy shocks single cylinder combustion engine driven machinery uniform generator, belt conveyor, light elevator,electric hoist, machine tool feed drive, ventilator, turbo-blower, turbocompressor, mixer (constant density) 1 1.25 1.5 medium shocks machine tool main drive, heavy elevator, crane turning gears, mine ventilator, mixer (variable density), multicylinder piston pump, feed pump 1.25 1.5 1.75 heavy shocks press, shear, rolling mill drive, heavy centrifuge,heavy feed pump, pug mill, power shovel, rotary drilling apparatus, briquette press 1.75 2 or higher 2.25 or higher
Kv	is a   dynamic factor which accounts for internally generated tooth loads induced by non-conjugate action of the teeth, by gear mesh stiffness variation, by gear imbalance and the like. The AGMA code defines a transmission accuracy level number,   Q, which reflects these latter (high Q implies low excitation, a low Q refers to low accuracy and high vibration) and suggests the   Kv factors shown below, expressing them empirically as follows (with velocity   v in m/s) :-   Q ≤ 5 Kv = 1 + √v/3.6       gears of this class are limited to speeds under 13m/s.   6 ≤ Q ≤ 11 Kv = ( 1 + √v / ( 7.6 - 4 B ) )B where   B = 0.25 ∗ ( 12 - Q )2/3   Q ≥ 12 Kv = 1     - this corresponds to ultra precision gearing, or to situations where dynamic loads have been accurately forecast and separately allowed for. The selection of a suitably realistic accuracy level requires considerable experience. Kv does not account for vibration induced by running near shaft critical speeds or by other resonances - these should be avoided or separately catered for. Note that the AGMA defines   Kv as the reciprocal of the Kv used here.
Km	is a   load distribution factor which reflects the non-uniformity of tooth loading over the face width of the teeth, arising from gear and mounting inaccuracy, elastic deformation of shafting and the like. For a face width f (mm) the AGMA proposes the empiricisms : Km = 1 + Cpf + Cma     where Cpf is a pinion proportion factor which reflects misalignment due to load induced elastic deformations of the pinion; it may be evaluated (with dimensions in mm) from : Cpf = 0.1 max( 0.5, f/D1 ) + max ( 0, f - 25 )/2000 - 0.025     graphed below. Cma is a mesh alignment factor which accounts for misalignment due to causes other than elastic deformation such as inaccurate location of shaft bearings. It is approximated : Cma = A + f/B - (f/C)2     in which the constants A, B & C for various classes of gears - open, commercial and precision enclosed - are shown below.

The face width should be reasonably proportioned to other gear dimensions. If a tooth is too wide it may bend excessively across its width, if it is too narrow then an uneconomically large diameter must be provided to compensate for lack of width. Proportions may be expressed as :-

( 16 )           f   =   β m       where, usually, 9 ≤ β ≤ 15 for economic gears -

These limits should not be regarded as inviolable, but costs should be expected to escalate if they are exceeded.