Screw thread mechanics

There are always three major components in practical applications of the screw thread mechanism :

• the   screw - a generic name applied to a setscrew, leadscrew, bolt, stud or other component equipped with an external thread,
• the   nut - refers to any component whose internal thread engages the screw, such as the nut of a nut & bolt or a large stationary casting with a tapped hole into which a stud is screwed, and
• the   thrust bearing - that is the contact surface between two components which rotate with respect to one another. Examples of thrust bearings include :
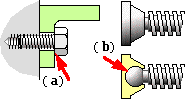
  1. the under-surface of a screw head which is being tightened by a spanner;
  2. the spherical seating of a G-clamp screw in the stationary self-aligning anvil.

Clearly 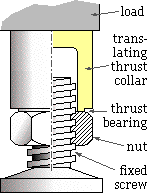there is relative motion in the thrust bearing, and also between the nut and the screw - and where there is relative motion there is   friction. We now examine the role of friction since it dominates the behaviour of the mechanism unless special ( read 'expensive' ) means are taken to minimise its effects. When considering friction it doesn't matter which component rotates and which is stationary - it's the   relative motion which is important. We shall therefore analyse the jack shown here to deduce the general effect of friction on screw thread behaviour.

The jack's screw is fixed; the nut is rotated by a spanner and translates vertically. The thrust collar's only motion is vertical translation as it is prevented from rotating by contact with the load, one corner only of which is pictured. Since there is relative rotation between contacting nut and collar, the contacting surface assumes the role of thrust bearing.

The nut shown here in plan is in contact with three bodies :

• the spanner exerts the torque   T which tends to raise the load ( analogous to tightening a nut and bolt )
• the screw thread which exerts the frictional torque   T_t , and
• the thrust bearing which exerts the frictional torque   T_b .

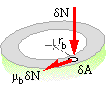
Consider the thrust bearing first. We shall assume that the contact surface of area   A is in the form of a narrow annulus of mean radius   r_b on which the uniform pressure is   W/A, where   W is the load supported by the mechanism. If the coefficient of friction in the bearing is   μ_b then the torque exerted by the frictional force on an area element δA is   δT_b   =   μ_b δN r_b   =   μ_b r_b ( W/A ) δA. Integrating over all the contact area
( ii)       T_b   =   W μ_b r_b

Consider now the thread which is square, of mean radius   r_m and lead angle   λ. The nut engages the screw with friction coefficient   μ corresponding to a   friction angle φ = arctan μ. The static and kinetic coefficients of friction are taken to be essentially equal for this preliminary analysis.

We wish to find the torque   T_t which must be exerted on the nut to offset thread friction and maintain the load   W in equilibrium - that is either static or moving at constant speed. A torque which tends to raise the load is reckoned positive; a negative torque is one which tends to lower the load.

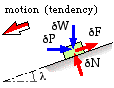
A small element of the nut is shown below sliding or about to slide on the inclined ramp of the thread, this motion being either up or down the thread. Both motion directions are sketched. δP is the small force on the element due to the torque, and the element supports a small part of the load   δW. The contact force components are the normal and friction forces,   δN and   δF - the latter opposing motion or motion tendency.

	The nut element free body requires for equilibrium . . .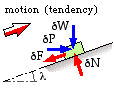
		normal to plane :	δN = δP sinλ + δW cosλ
		parallel to plane :	δF =   δP cosλ - δW sinλ		δF = - δP cosλ + δW sinλ
	If the element is moving, or on the point of motion, then   δF = μ δN   and so
		eliminating   δF, δN :	δP = δW tan ( λ + φ )		δP = δW tan ( λ - φ )
	The total torque   Tt is the sum   Σ rmδP over all the identical nut elements, ie.
( iii)		. . . . if motion (tendency) is	Tt = W rm tan ( λ + φ )             upwards		Tt = W rm tan ( λ - φ )             downwards

When raising a load the thread inclination   λ is thus effectively steepened by the thread friction angle   φ.

The upward tightening torque from ( iii) is plotted here against friction coeffficient for a lead angle,   λ = 0.25 ( 14.3^o ).
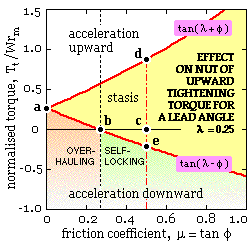
When there is negligible thread friction ( φ = 0 ) then   T_t /Wr_m = tanλ = 0.255, the point a.
The equilibrium line a-d corresponds to incipient motion up the thread; the equilibrium line a-b-e corresponds to incipient motion down the thread. The area between these lines represents stasis ( δF < μ δN ); the areas beyond the lines correspond to non-equilibrium, ie. to acceleration - though it should be realised that only thread friction is being considered at this point.

Consider what happens if the coefficient of friction is 0.5 for example. Before any torque is applied ( T_t = 0 ) the nut is at rest, point c. The torque is thereafter increased until at d the nut breaks away and rotates up the thread at constant velocity. If the torque were to increase further then the nut would accelerate.
If however at c the torque were to increase in a negative sense - to 'undo' the nut, assisted by the load - then when point e was reached the nut would break away and move down the thread at uniform speed. Any further increase of torque in the negative sense would lead to downward acceleration.

The point b is significant. It corresponds to the critical coefficient of friction for the lead concerned,   μ_c = tanλ,   at which the nut is on the point of moving down the thread of its own volition without any torque applied ( T_t = 0 ). Further, if . . .

μ>μc	then the thread is   self-locking in that the nut cannot undo by itself, it needs to be unscrewed by a definite negative torque; or
μ<μc	then the thread is   overhauling in that the nut will unscrew by itself under the action of the load unless prevented by a positive tightening torque.

Clearly self-locking behaviour is essential for threaded fasteners. Car lifting jacks would not be of much use if the load fell as soon as the operating handle was released - so they too demand self-locking characteristics.
Some applications of power screws require overhauling behaviour. The Archimedean drill (above) and pump action screwdrivers (below) incorporate very large lead angles which guarantee that the critical friction coefficients are larger than any actual coefficient likely to be encountered. Sensitive linear actuators may incorporate recirculating ball screws such as that illustrated on the left to reduce thread friction to levels which go hand- in- hand with overhauling.

Efficiency is important in rotary/ linear motion transformation such as provided by power screws. Whilst acting against a load, the efficiency of a screw thread alone ( ie. neglecting the thrust bearing ) is :
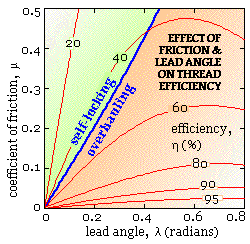
            η   =   W_{for a given Tt} / W_{for the same Tt without friction}
                  =   tan λ / tan( λ + φ )       from ( iii)

The effect of lead and friction on thread efficiency is plotted here - as expected, high efficiencies demand very low friction. Also shown is the line of critical friction.

Coefficients of friction around 0.1 to 0.2 may be expected for common materials under conditions of ordinary service and lubrication - steel on steel for fasteners, and steel on bronze or cast iron in the case of power screws. Special coatings and surface treatments can reduce friction significantly. Vibration also reduces friction and can cause fasteners to unloosen unless locked as mentioned above.
Lead angles around 3^o are typical of single start power screws which are therefore somewhat inefficient - this is one reason for multiple start screws with their associated large leads.
 

From ( i), ( ii) and ( iii) the total torque necessary to raise a load   W whilst overcoming thread and thrust bearing friction is :

( 2)         T   =   W [ r_m tan( λ + φ ) + μ_b r_b ]

The foregoing analysis has been developed for square threads ( α = 0 ), but ( iii) and ( 2) may be applied with little error to Acme threads ( α = 29^o ), and also to ISO Metric fasteners ( α = 60^o ) provided the effect of wedging ( analogous to V-belts ) is included - thus the effective coefficient of thread friction to be used in ( 2) is   μ sec( arctan( cosλ tan^α/₂ )), which tends to   μ sec^α/₂ for small lead angles.

Static failure

• the first figure is   S_u /100 where   S_u is the steel's nominal tensile ultimate (MPa)
• the second figure is the ratio   S_y /S_u   where   S_y is the nominal 0.2% offset yield strength.

It is difficult to determine the yield of a full size threaded connector ( as opposed to a cylindrical test piece ) because of the different strain rates of shank, thread and runout. For this reason the proof stress rather than the yield stress is used as a criterion for failure assessment - the   proof stress   S_p is the largest stress which does not lead to any permanent set. The proof load of a screw made from a particular material is the maximum load the screw can withstand without permanent deformation, and is given by ( 1) as the product of stress area ( Table 1 ) and proof stress ( Table 2 ). Selection of class 12.9 should not be undertaken lightly - its high strength begets other potential problems.

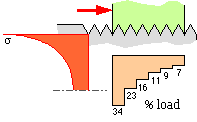
We have noted that the elastic behaviour of connected members has a significant effect upon the distribution of load between their connectors. In an elastic bolt and nut connected by a number of thread turns, the first 'thread' takes a disproportionate fraction of the total tensile load - Craddock   op cit reports the load distributed among the threads as sketched here. It is clear that there is little benefit from an engagement length exceeding half-a- dozen threads. Special nuts which alleviate non-uniform load distribution are available. The variation of normal stress   σ over a cross- section adjacent to the nut face ( as sketched ) is dominated by stress concentration induced by the thread root, so it is hardly surprising that bolt fractures usually occur in the exposed threads close to the nut face.

Another failure mechanism is stripping of the nut threads, which is essentially shear failure of the nut material on the cylindrical surface at the thread major diameter. Stripping of the bolt threads is a similar shear of the bolt material at the minor diameter - but this is rare. Other possible failure mechanisms, such as crushing of the nut bearing surface and dilation of a thin nut due to its riding up the thread flanks, are not critical in themselves, but contribute to other modes.

If any failure is to occur, then bolt fracture is the preferred mode. Bolt fracture is clearly discernable and often occurs whilst tightening, when torsional shear stresses ( which dissipate quickly after tightening ) are superimposed upon tensile stresses. So the operator replaces the bolt and learns to exercise care in subsequent tightening. Thread stripping on the other hand is insidious and progressive - the first thread fails putting more load onto the remaining threads, hence the second succumbs . . . and so on. When threads strip it is often difficult to separate components for fastener replacement, whereas a broken bolt requires no further separation. The consequences of a tapped hole in a car engine block being stripped by over- zealous spanner wielding is a case in point.

For a given load, bolt fracture tendency will clearly be reduced by a larger stress area ( ie. a larger bolt size ) and/or a higher class of material. Given these parameters ( load, size and bolt class ), nut stripping will be reduced by a longer nut and hence an increased cylindrical shear area, by a thicker walled nut to decrease dilation, and/or by a superior nut (property) class.

The first stage of fastener design is bolt selection - size, class and other geometric attributes. ISO Metric nuts have been dimensioned to bias any failure towards bolt fracture rather than nut stripping, on the tacit presumption that the nut class is equal to or greater than the bolt class - ie. the material of the chosen nut is at least as strong as the preselected bolt's material. It is for such reasons that regular nut lengths are about 80% of bolt size, and of the hexagonal dimensions shown in Table 1 - though there are various styles of nut which differ from these figures.