Loads in an elastic bolted assembly

The safety of a threaded fastener depends upon the actual load on it and the maximum load it can withstand. The latter has been considered above. Since the fastener is part of an indeterminate assembly it is now necessary to analyse such an assembly to find out just what is the actual load on the fastener itself.
The analysis is very similar to that carried out in an earlier chapter in the context of indeterminate assemblies.

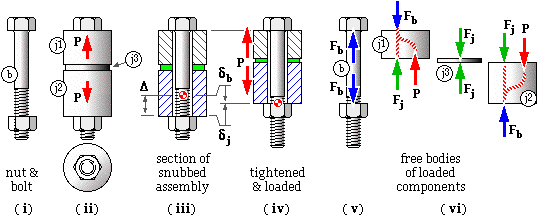
The nut and bolt b ( i) are used to connect together three joint-members j1, j2 and j3 ( ii). After tightening the nut by a known amount   Δ, the external load   P is applied axially to j1 and j2, and tends to separate the joint members. Joint separation must usually be avoided, so examination of the assembly has two major goals :

• to determine the assembly's tendency towards separation, and
• to ascertain the safety of all components of the assembly.

Compatibility

Shown in section ( iii) is the unloaded free assembly with the nut 'snubbed' ( finger tight ) - that is the nut has been tightened to close up all gaps in the assembly without inducing appreciable loads. An imaginary mark is situated on the thread a distance   Δ from the nut underside. After tightening, this mark will coincide with the nut face, so   Δ represents the distance moved by the nut along the bolt thread during the tightening operation. After tightening and loading by the external force, the disposition of the assembly elements is shown   much exaggerated in ( iv). The extension of the bolt is   δ_b while the compression of the joint   δ_j is the sum of its elements' contractions, ie.   δ_j   =   δ_j1 + δ_j2 + δ_j3.
From the geometry of ( iii) and ( iv), compatibility necessitates :
        Δ   =   δ_b + δ_j

Equilibrium

The free body of the bolt and nut ( v) illustrates the unknown forces at the bolt's two contacts. The upper   F_b is the axial resultant of the uniformly distributed pressure exerted by the top surface of j1 over the annular area under the bolt head. The other contact - the upper surface of the nut bearing on the underside of j2 - yields a similar pressure resultant whose magnitude must also be   F_b for equilibrium of the bolt.
The free body of the joint element j3 in ( vi) shows the unknown pressure resultant   F_j due to annular contact with its neighbours. The reactions to the aforementioned   F_b and   F_j appear on the remaining free bodies j1 and j2 in ( vi) from either of which results :
        P   =   F_b - F_j

Evidently the bolt is under tension   F_b.
Parts of the joint components j1 and j2 in contact with the nut and bolt are also subjected to the bolt load   F_b, however for the case considered, the majority of these components, and all intermediate components such as j3, are subjected to the compressive load   F_j only. We shall here assume that all joint components are wholly compressed by   F_j - this approximation should be reviewed for other arrangements.

Constitutive laws

Bolt - Since in the previous steps the bolt is loaded by the tensile force   F_b and undergoes the tensile deformation   δ_b, then, if   k_b is the axial stiffness of the bolt :
        F_b   =   k_b δ_b
Joint - Since in the previous steps the joint is loaded by the compressive force   F_j and undergoes the compressive deformation   δ_j, then, if   k_j is the stiffness of the joint - that is of the three joint- elements in series   1/k_j = 1/k_j1 + 1/k_j2 + 1/k_j3 :
        F_j   =   k_j δ_j

Solving these four equations resolves the indeterminacy, giving the component loads :

( 3a)         F_b   =   F_i + P k_e /k_j     where     1/k_e   =   1/k_b + 1/k_j ;     F_i   =   k_e Δ
                    F_j   =   F_i   - P k_e /k_b

k_e is the   equivalent stiffness of the assembly ( k_e < k_b & k_j ). Evidently the bolt is in series with the joint, ie. all four components are in series. F_i is the initial load ( or   preload ) in the assembly due to tightening the nut by an amount   Δ.

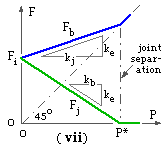
The bolt load   F_b and the joint load   F_j from ( 3a) are plotted in ( vii) versus the external load   P, with k_e < k_b < k_j.
When the external load is zero then   F_b = F_j = F_i and the load path is a closed loop through all elements in series. As the external load increases then the joint- elements become less tightly compressed -   F_j decreases - while the bolt load increases. For the case considered, the rate of bolt load increase   k_e /k_j is less than the rate of joint load decrease   k_e /k_b, because   k_b < k_j.

The graph indicates that the joint force becomes zero when the external load reaches some critical value   P*. Since   F_j cannot be tensile ( negative by the present convention ) it follows that j3 must lose contact with the other two joint components. Thus joint separation occurs and the bolt takes all the external load, as may be confirmed by free bodies. So, after separation,   F_j = 0 and   F_b = P.

In the arrangement of ( viii) the assembly is required to sustain the external load   P_o without separation, but the preload and stiffnesses are such that   P_o exceeds the separation load   P* so the requirements cannot be met - a larger separation load is necessary.
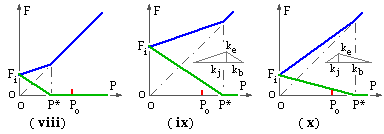
One way of increasing the separation load is to increase the preload   F_i as in ( ix). The slopes of the bolt and joint load characteristics are not altered by this extra tightening. Another approach ( x) uses the same preload as ( viii) but with an increased stiffness ratio   k_b / k_j. Clearly it is easier to alter the preload ( within the strength capabilities of the bolt and joint components ) than it is to alter stiffnesses.

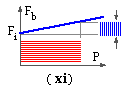
In a fatigue situation with given alternating load on the assembly, P, the amplitude of the damaging fatigue load on the bolt   F_b is reduced as the slope of the F_b -P characteristic is decreased ( xi). Comparing the arrangement ( ix) with ( x) it is apparent that when designing for bolt fatigue, the low-slope arrangement ( ix) is preferable - that is a relatively low bolt stiffness   k_b and high preload   F_i are desirable.

The stiffness of an elastic component which is subjected uniformly to tension or compression is
        k   =   F/δ   =   AE/L
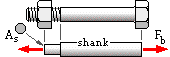
A bolt may be reckoned as two elements in series, each with a constant cross-sectional area - the shank, and the exposed thread whose area is the stress area   A_s. The lengths of these should include half the head and nut thicknesses respectively, to allow for local deformation. The stiffness of short bolts is less predictable than that of long bolts.

A gasket is a thin compliant sheet rather similar to j3 above, which is sandwiched between other joint components to fill up microscopic irregularities thus preventing fluid leakage. If the fastened components include a gasket, then determination of their stiffness can pose problems - we shall consider gasketed joints separately below.

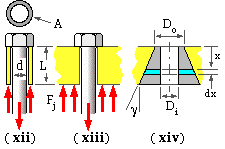
In a metal-to-metal ( non-gasketed ) joint, calculation of a fastened component's stiffness is straightforward if it is a thin tube and the external load is applied uniformly over the annular end area   A as at ( xii) - but this is unusual. More commonly the component is similar to ( xiii). Known are its thickness   L and the fact that there is extended reactive contact over the face which is not in contact with the bolt head or nut face. The component may be modelled as a conical frustum ( xiv) of diameter   D_o at the small end and cone angle   γ, bored cylindrically with diameter   D_i to clear the bolt. The deformation   dδ of a small element, thickness   dx, will be :
        dδ   =   F_j /k_x   =   F_j ( L/EA )_x   =   F_j dx / E ^π/₄ [ ( D_o+2x.tanγ)² - D_i² ]

Integrating, the total compressive deformation   δ over length   L is found to be :
        δ   =   ( F_j /π E D_i tanγ ) ln[ ( D_o - D_i + 2L tanγ )( D_o + D_i ) / ( D_o + D_i + 2L tanγ )( D_o - D_i ) ]

It is usual to particularise this for some assumed cone angle such as 30^o, but a general result has been obtained by Wileman op cit using finite elements on the basis of   D_i ≈ d ( small clearances ) and   D_o ≈ 1.5d - ie. the outer diameter of the annular bearing area under the hexagon equals the standard width across flats, Table 1. Wileman's results may be correlated for steel by :

( 4)       k   =   F_j /δ   ≈   Ed ( 0.702 +0.654 d/L ) / ( 1 - 0.12 d/L )   ;     d/L ≤ 2

Use of ( 4) presumes that there is sufficient material present to allow the lines of force to develop unfettered by finite boundaries.