Preload and its control
( following Bickford op cit )
The benefits of high preload were apparent in ( ix) above - tendency towards separation ( or leakage in a pipe joint ) is reduced, fastener loosening is minimised and so on. Furthermore it is better to use highly stressed small bolts rather than lightly loaded large bolts because the stiffness of the small bolts is less. In general, preload should be as high as components can withstand. Bolt preload is usually specified between 75% to 100% of proof, with 90% being common. Thus for an M16x2 class 8.8 screw the proof load is As Sp = 157x590 = 93 kN and so a suitable preload is 0.9x93 = 83 kN. Which is all very easy . . . . but how do we ensure that the nut is tightened to produce 83 kN in the field? What measuring devices can be used to control preload?
Bickford puts it neatly thus :
| |
'When we tighten a bolt,
( a) we apply torque to the nut,
( b) the nut turns,
( c) the bolt stretches,
( d) creating preload.'
|
|
Ideally we would like to measure preload directly ( d) and advise the spanner operator when the required preload is reached. However in practice, feedback is usually from an earlier step, and some of the difficulties which this causes are now examined.
Torque wrenches are commonly used to monitor the torque applied to a nut being tightened - step ( a) of Bickford's sequence. We may employ ( 2) to obtain an indication of the spanner torque T necessary to induce the preload Fi.
The pitch of ISO Metric fasteners in the sizes of most practical interest lies between 0.12d and 0.16d ( Table 1 ) and correspond to lead angles λ around 2-3o. The thread mean diameter is dm = ( d + d1 )/2 = d - 5h/8 = d -0.5413p so, assuming p ≈ 0.14d then the mean thread radius is rm ≈ 0.46d.
The annular contact area under the nut hexagon plays the role of thrust bearing. Its OD is about 1.5d as may be inferred from Table 1, so the mean bearing radius is rb ≈ ( d +1.5d)/4 = 0.63d. Assuming the same coefficient of friction μ in nut bearing and in threads, ( 2) on expansion with the neglect of small lead angles becomes :
( 2a) T = Fi ( rm ( p/π dm + μ sec30o ) + μ rb ) = Fi d ( 0.022 + 0.53μ + 0.63μ ) = K Fi d
The three terms in the penultimate RHS here represent three portions of the tightening torque :
- the torque useful in 'raising the load' ie. in generating preload ( 0.022 or 10% )
- the reaction torque dissipated in thread friction ( 0.53μ or 40% )
- the torque used in overcoming nut bearing friction ( 0.63μ or 50% )
The percentages quoted refer to an average friction coefficient around 0.15. Only some 10% of the applied torque generates preload - and herein lies the cause of most joint problems. Preload is what's left of the tightening torque after friction has absorbed the lion's share, since preload cannot be induced until motion has occurred. Anticipated variations in the coefficient of friction will thus have a marked effect upon the preload, and careful calibration of the torque wrench will do little to improve preload accuracy.
| | Nut factors
|
| | Steel Thread Condition | K
|
| | as received, stainless on mild or alloy | 0.30
|
| | as received, mild or alloy on same | 0.20
|
| | cadmium plated | 0.18
|
| | molybdenum-disulphide grease | 0.14
|
| | PTFE lubrication | 0.12
|
Mean values of reported nut factors K in ( 2a) are tabulated here to give an appreciation of the beneficial effect of proper lubrication of thread and nut face on preload. Variations of ±25 % in K are routinely experienced; larger variations are not unexpected. Ideally, each application should be tested to determine its own peculiar nut factor since the factor includes the effects of everything that affects the torque- to- preload transformation, not just friction but also the consequences of local deformations, interrupted tightening, inaccurate thread form, misaligned components, relaxation due to tightening other bolts in the joint, whether the fastener is new or is being reused, initially bent bolts, speed of tightening etc. etc. - all of which affect preload reproducibility. It is concluded that torque wrenches may be quite adequate for everyday non-critical tightening operations such as those on vehicles, but the measurement of torque, step ( a), is by itself inadequate when preload accuracy is needed.
The measurement of nut rotation θ - Bickford's sequence step ( b) - suggests itself as an alternative guide to the preload attained, since the distance Δ moved by a nut along the ( single start ) thread is pitch ∗ nut rotation, ie. with ( 3a) Fi = ke Δ = ke pθ. However this rotation- preload correlation requires linear behaviour of the joint ( ke ) - and this usually does not happen.
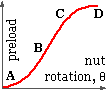 Instead, a characteristic along the lines of the sketch can be expected. At low loads A-B, non-linearities arise chiefly from warp straightening and embedment of contact surface peaks. In the middle range B-C, linear elastic behaviour predominates, as suggested by the foregoing theory. Finally at high loads, progressive yielding of the various components produces the non-linearities C-D. It is evident therefore that counting turns is also an unsatisfactory preload monitor, unless one knows the Fi-θ relationship - the measurement of which rather begs the question.
Instead, a characteristic along the lines of the sketch can be expected. At low loads A-B, non-linearities arise chiefly from warp straightening and embedment of contact surface peaks. In the middle range B-C, linear elastic behaviour predominates, as suggested by the foregoing theory. Finally at high loads, progressive yielding of the various components produces the non-linearities C-D. It is evident therefore that counting turns is also an unsatisfactory preload monitor, unless one knows the Fi-θ relationship - the measurement of which rather begs the question.
Measuring bolt stretch - step ( c) - would seem to be more direct than measuring torque or turns. Ultrasonic measurement of bolt length changes whilst tightening are routinely carried out - the reader is referred to Brown op cit. Heat exchanger joints are typical subjects for this, but they employ many bolts and it is impossible to apportion preload uniformly between the bolts. Thus one bolt might be tightened with the correct stretch and preload, but tightening subsequent bolts causes that preload to change. So complex tightening sequences have to be resorted to - and even then preload variation between individual bolts can be very large.
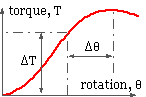
Industrial bolt tighteners may be computer controlled and often monitor both torque and turn. They first apply a specified torque ΔT to overcome initial warpage and embedment, thereby ensuring the bolt is taken into the elastic zone. The nut is then rotated through a specified rotation Δθ to ensure the bolt yields - this results in a preload which is relatively predictable, ie. insensitive to the vagaries of tightening. Although the bolt has yielded, eventual dissipation of torsional tightening stresses together with bolt ductility ensures that it is still capable of sustaining significant loads - though careful joint design is required. Computer controlled tightening using this technique can be programmed to automatically sense and warn of stripped or crossed threads, holes which are blind or inadequatedly tapped etc.
The most direct control of preload is of course to measure preload itself, Bickford step ( d). Special crush washers ( akin to wavy washers ) may be designed to flatten at the desired preload so that control is exercised by visual inspection. But these also have drawbacks - while they indicate when a certain preload has been attained, they cannot advise by how much it has been exceeded.
 Copyright 1999-2005 Douglas Wright,
doug@mech.uwa.edu.au
Copyright 1999-2005 Douglas Wright,
doug@mech.uwa.edu.au
last updated May 2005
 Instead, a characteristic along the lines of the sketch can be expected. At low loads A-B, non-linearities arise chiefly from warp straightening and embedment of contact surface peaks. In the middle range B-C, linear elastic behaviour predominates, as suggested by the foregoing theory. Finally at high loads, progressive yielding of the various components produces the non-linearities C-D. It is evident therefore that counting turns is also an unsatisfactory preload monitor, unless one knows the Fi-θ relationship - the measurement of which rather begs the question.
Instead, a characteristic along the lines of the sketch can be expected. At low loads A-B, non-linearities arise chiefly from warp straightening and embedment of contact surface peaks. In the middle range B-C, linear elastic behaviour predominates, as suggested by the foregoing theory. Finally at high loads, progressive yielding of the various components produces the non-linearities C-D. It is evident therefore that counting turns is also an unsatisfactory preload monitor, unless one knows the Fi-θ relationship - the measurement of which rather begs the question.
