DANotes: Welded joints: Unified analysis

Unified analysis

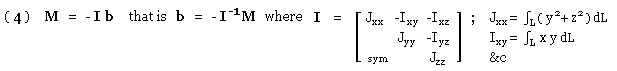
The theory will be developed in three dimensions, and later particularised to two.

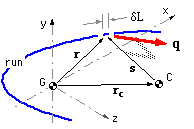
A general three-dimensional run of length L is illustrated, in which a typical element δL is located at r in a convenient centroidal Cartesian system, the centroid being such that :-
( iii) ∫_L r dL = 0 ; r = [ x y z ]' see ( i) above.

The centroidal loading F & M causes the loaded member to rotate with respect to the support about a fixed centre of rotation C located at r_c, so the radius s from C to the element is
( iv) s = r - r_c
As a result of this rotation, compatibility requires that the strain in the joint at the element is both orthogonal to and linear in s. Presuming elastic behaviour, the stress resultant at the element - ie. the intensity q - is also orthogonal to and linear in s. This may be expressed as :

( 2) q = [ q_x q_y q_z]' = b x s = b x r - c using ( iv)
where b = [ b_x b_y b_z]' is a vector constant commensurate with linearity,
the cross product ensures q, s orthogonality, and
c = b x r_c = [ c_x c_y c_z]' is another constant vector common to all elements.

Equation ( 2) establishes the form of the intensity variation with position r along the run. It remains to evaluate the two constants b and c to define completely the dependence of q upon r. This evaluation follows from equilibrium :-

For force equilibrium, using ( 2)
F = [ F_x F_y F_z]' = - ∫_L q dL = - ∫_L ( b x r - c ) dL
= - b x ( ∫_L r dL ) + c ∫_L dL ; the first integral vanishes as a result of ( iii), leaving

( 3 ) F = L c that is c = F / L - just the reversed primary intensity of the traditional method.

For moment equilibrium, again using ( 2)
M = [ M_x M_y M_z]' = - ∫_L r x ( q dL) = - ∫_L r x ( b x r - c ) dL
= - ∫_L r x ( b x r ) dL + ( ∫_L r dL ) x c ; in which the second integral vanishes, again via ( iii).
Expanding out the products in the first integral and integrating term by term (this is left as an exercise for the reader) :-

This matrix of second line-moments can be computed from known geometry.

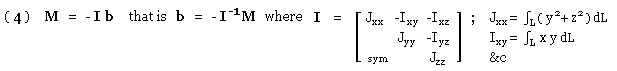
The constants b and c may thus be determined from known loading and run geometry, via ( 3) and ( 4), enabling q to be found at any point r from ( 2).

In the case of a two-dimensional joint lying wholly in the x-y plane (the only case examined at length here), z vanishes everywhere on the run, r degenerates to [ x y 0 ]', and ( 4) becomes :-
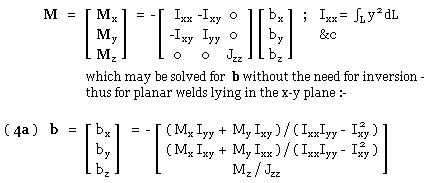
b vector
It may be shown that equations ( 2), ( 3) and ( 4a), with I_xy = 0, reduce to the equations cited previously in the traditional approach. However ( 4a) correctly recognises x-y coupling, as may be seen by comparing it with the equations used for the asymmetric bending of beams.

Resolution

The intensity q at a point in the joint run is related to the known load in global terms [ q_x q_y q_z ]', via ( 2). Safety at that point in turn depends, via ( 1), on q expressed in terms of local components [ q₁ q₂ q₃ ]' whose directions are dictated by the orientation of the fillet locally at the point. To avoid the need for visual inspection to carry out the global -to -local transformation - inspection which can be awkward as the above traditional example showed - we define the matrix operation :-

( 5 ) q_local = t q_global ie. [ q₁ q₂ q₃ ]' = t [ q_x q_y q_z ]'
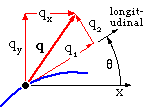
in which the 3x3 transformation matrix, t, is a pure geometric entity involving the direction cosines of the run tangent at the point in question, together with the roll angle of the fillet. We consider resolution only for the particular case of a run lying in the x-y support plane with the z- and 3-senses identical (as above). The fillet does not roll. If θ is the inclination of the longitudinal sense (tangent to the run) in the x-y system - θ being reckoned positive anti -clockwise from the x to the longitudinal sense - then :

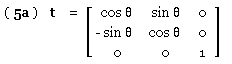
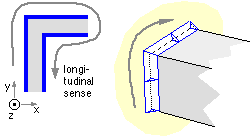
t matrix traverse sense
The longitudinal sense may be remembered by the requirement for the run to be traversed clockwise when the weld plane is viewed normally, as sketched:

Summary

The unified approach to analysing a fillet welded joint whose run consists of co-planar straight line segments involves the following steps :

erect a convenient X-Y system in the run plane and calculate the centroidal coordinates
erect a parallel centroidal x-y system as the basis for further work
- determine the centroidal second moments of run length
- define the joint loading at the centroid, probably using a free body
- calculate the constants b and c from ( 4a) and ( 3) respectively
for each straight line run segment :
- determine the positive longitudinal sense, the slope θ and the t-matrix from ( 5a) :
- for each of the two end points of the lines in turn :
  - determine the radius vector r from the centroid
  - compute q in global Cartesian terms from ( 2)
  - ascertain the local q components from ( 5) and
  - calculate the equivalent intensity using ( 1)
search over all end points for the maximum value of q_e (corresponding to minimum safety) then apply the design equation ( 1) to find either the safety factor n in the analysis situation or the necessary fillet size w in the design situation.

The foregoing example carried out inappropriately by the traditional technique is repeated here using the unified method, and highlights how neglect of asymmetry can lead to a dangerous situation. Thus if asymmetric bending had been incorrectly neglected here (eg. zero I_xy used in calculations) then a fillet size of 2.8 mm would have resulted, which, if used in the joint, would have yielded an actual safety factor of only 2.8^_*410 / 2^_*464 = 1.24 - a significant and dangerous reduction from the target of 1.73.

Conclusion

The foregoing analyses rest upon rather simplistic foundations despite the apparent mathematical niceties. Three significant and questionable assumptions are the following :

The connected members are assumed to be rigid, the weld metal itself being the only compliance in the connection - however the compliant lap joint modelled in the Appendix demonstrates that stress concentration must occur when all components in the connection undergo deformation, as would happen to some extent in any practical fillet welded joint.
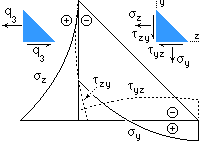Stresses in the throat plane are assumed to be uniform over that plane. It is possible to define a more realistic stress distribution which satisfies equilibrium, compatibility and linear elastic behaviour everywhere within the fillet. The variations of the stress components on the fillet legs predicted by one such model are sketched here for q₃ loading. Significant normal 'bending' stresses evidently occur in the horizontal leg, even although their force resultant is zero. The high stresses in way of the geometric singularity at the root are noteworthy. Similar stress concentration occurs with q1 loading, however such models (again) neglect compliance of the joined components - currently the effect of this can only be examined numerically, by finite elements for example.
It will be seen in the context of Fracture Mechanics that the stress concentration ahead of any crack tip is extreme due to the geometric singularity. A crack is inherent with filleted joints - the tip coinciding with the fillet root - so it is inevitable that at low loads the material will yield and behave non -linearly over a small region with some consequent stress redistribution.

These assumptions notwithstanding, the theory works in practice because it describes fairly well joints' tendencies to failure - so provided it is used with experimental safety constraints which also are characterised by the theory, then safety assessment is perfectly valid.

This chapter cannot conclude without reiterating forcefully that successful welded joint design relies as much if not more on common sense and practical experience than on mathematics - no matter how appealing this last might be.


The longitudinal sense may be remembered by the requirement for the run to be traversed clockwise when the weld plane is viewed normally, as sketched: