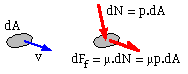 moving past at velocity v. Since sliding must occur the force resultant on dA comprises the elemental component dN = p.dA orthogonal to dA together with the elemental friction component dFf = μp.dA coplanar with dA and in the sense of v.
moving past at velocity v. Since sliding must occur the force resultant on dA comprises the elemental component dN = p.dA orthogonal to dA together with the elemental friction component dFf = μp.dA coplanar with dA and in the sense of v.
Before examining a practical twin-shoe brake we must understand the behaviour of a single shoe.
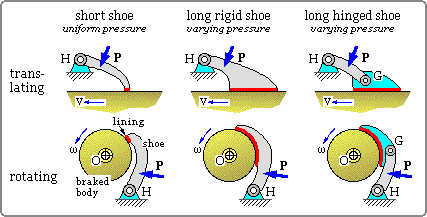 Various shoe configurations are illustrated. Each consists of a body whose motion is braked together with a shoe which can swing freely about a fixed hinge H. A lining is attached to the shoe and contacts the braked body. The actuation force P applied to the shoe gives rise to a normal pressure and corresponding braking friction distributed over the area A of contact between lining and braked body.
Various shoe configurations are illustrated. Each consists of a body whose motion is braked together with a shoe which can swing freely about a fixed hinge H. A lining is attached to the shoe and contacts the braked body. The actuation force P applied to the shoe gives rise to a normal pressure and corresponding braking friction distributed over the area A of contact between lining and braked body.
The illustration below explains this contact in more detail. An element dA of the lining is shown with the braked body
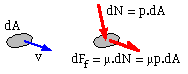 moving past at velocity v. Since sliding must occur the force resultant on dA comprises the elemental component dN = p.dA orthogonal to dA together with the elemental friction component dFf = μp.dA coplanar with dA and in the sense of v.
moving past at velocity v. Since sliding must occur the force resultant on dA comprises the elemental component dN = p.dA orthogonal to dA together with the elemental friction component dFf = μp.dA coplanar with dA and in the sense of v.
Shoes are classed as being either short or long. A short shoe is one whose lining dimension in the direction of motion is so small that contact pressure variation is negligible, ie. the pressure is everywhere uniform, at pm say. The contact resultant therefore consists of the normal reaction N = Σ dN = Σ p dA --> ∫ p dA = pm ∫dA = pm A together with the friction force Σ μdN = μ.pmA. Short shoes are statically determinate.
In a long shoe the variation of contact pressure in the direction of motion is not negligible and integrals of the above form ( ∫ pdA ) cannot be evaluated unless the p-variation is known. A long shoe is thus statically indeterminate and must be appraised by the three -pronged attack used for cylinders, welds, thick curved beams and so on - a plausible spatial distribution of lining deformation ( geometric compatibility ) is first assumed, then the lining constitutive law ( presumed elastic ) and finally equilibrium are applied to establish completely the pressure variation for a given actuation. Long shoes are more complex than short.
The pivot G of a hinged shoe introduces a second degree of freedom permitting the lining to adopt a position which tends to spread wear more uniformly over the lining and hence to increase lining life.
The braked body may translate or it may rotate about a fixed shaft axis O. External rotational shoes only are sketched above - the treatment of internal shoes is identical to that of external.
All these configurations behave qualitatively in identical fashion, and they are all analysed in a similar manner - it's only their differing geometries which introduce complications. We shall lead up to the analysis of practical rotational long shoes by first considering the following simpler cases
| - | translational shoes - although these are uncommon since mechanical power is usually transmitted rotationally, they are geometrically simpler than rotational shoes, and |
| - | short shoes - although these are generally impractical because of their small lining area ( recall the 'Linings' section above ), they are simpler than long shoes as contact pressure is uniform. |
A shoe behaves very differently depending upon whether it trails or leads. If the braked body drags the lining away from the hinge then the lining trails behind the hinge and the shoe as a whole is said 'to trail.' The shoes in the lower row of the above sketch all trail while the shoes in the upper row all lead for the motion senses drawn.
In each of the following shoe analyses, the shoe geometry is defined and the coefficient of friction μ between lining and braked body is known. In the first instance it is required to find the resultant of the lining/braked-body contact for a given actuation. Determination of the braking effect, shoe performance parameters, and hinge & shaft reactions is thereafter straightforward.
It is useful to realise that effect is always proportional to cause for constant geometry and friction coefficient - thus if a shoe's actuation is doubled then the braking effect, lining pressure, hinge reaction etc. all double.
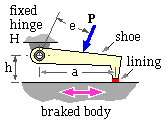
The geometry of a short translational shoe is sketched. The uniform pressure over the contact area A is pm . The braked body may move in either direction at a fixed distance, h, from the hinge axis.
Free bodies of the shoe are shown for the two possible directions - evidently the shoe in the left configuration trails while that in the right leads. The three contacts which each free body makes with its surrounds are
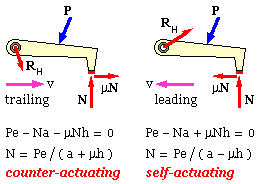
The normal reaction depends upon the moment Pe rather than on P itself. The product Pe is termed the actuation moment, M, so the two equilibrium equations may be written
( iii) N = pm A = M / ( a ± μh ) - the sign depending upon whether the shoe trails or leads
All terms on the RHS of this equation are geometric - apart from the actuation and the (presumably constant) friction coefficient - so the normal reaction and the frictional braking force are directly proportional to the actuation. The difference between the two behaviours is as follows
Once the normal and friction forces have been found via ( iii) for a given actuation, the hinge reaction, RH, may be ascertained easily from force equilibrium of the shoe free body. All forces are then known, allowing safe design to be carried out.
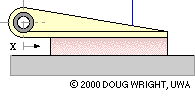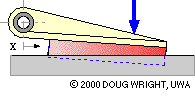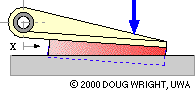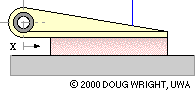
The lining thickness and compliance of this translational long shoe are grossly exaggerated to demonstrate how lining deflection varies in response to changing actuation. For a given actuation the deflection at any point along the lining is approximately proportional to the point's distance x from the hinge, with the maximum deflection occuring at the end of the lining furthest from the hinge. Assuming the lining to behave elastically, the compressive stress and the contact pressure p are also proportional to x. This proportionality is a reasonable postulate for practical linings which are not wholly elastic.
A long shoe is analysed by dividing it up conceptually into infinitessimal elements - each of whose contact with the translating body is identical to that of the short shoe above - then summing (integrating) the equilibrating effect of all the elements.
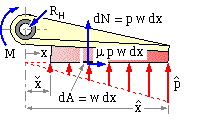
The free body of the long shoe is similar to that of the short in having three contacts, however the contact with the braked body is distributed. Consider such a trailing shoe whose lining, of constant width w normal to the sketch plane, extends from xmin to xmax as sketched { nomenclature explanation}. The lining pressure is p on the typical element of length dx located at x from the hinge, so the normal force on the element is dN = p.dA = p w dx, while the corresponding friction force will be μ p w dx.
Moment equilibrium of the assembly of elemental short shoes about the hinge (to eliminate the as yet unwanted hinge reaction) requires
M - Σ dN.x - Σ μdN.h = 0 or in the limit on substituting for dN : M = w ∫ p ( x + μh ) dx
Integration is possible only if the pressure distribution p(x) is known, so the above- noted proportionality between pressure p and distance x is formalised as p = pmax ( x / xmax ) - the severity of contact loading being characterised by the peak pressure pmax which depends upon the actuation. Inserting this into the equilibrium equation and integrating between the lining limits xmin and xmax leads to
( iv) pmax = ( M xmax / w ) / [ ( xmax3 - xmin3 )/3 + μh ( xmax2 - xmin2 )/2 ]
The relation ( iv) for a long shoe is similar to ( iii) for a short shoe as it expresses the essential proportionality between actuation and the resulting contact effects - if the actuation is doubled then the peak pressure pmax and the pressures at all points of the lining are also doubled. The total braking effect, hinge reaction etc. produced by a certain actuation follow from ( iv) - for example
total braking effect = Σ μpw dx = ∫ μ [ pmax( x/xmax )] w dx
= μ w pmax ( xmax2 - xmin2 ) / ( 2 xmax ) or substituting for pmax from ( iv)
= M / [ h + 2 ( xmax3 - xmin3 ) / ( 3 μ ( xmax2 - xmin2 ) ) ]
The details of this final result notwithstanding, it is clear that the braking effect is again proportional to actuation since only constant geometric and frictional terms occur.
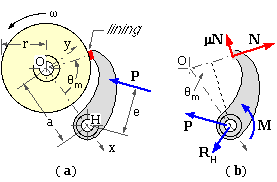
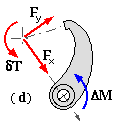
Turning now to drum brakes, we first consider the external, trailing short shoe sketched at ( a). The drum of radius r is centred at O which forms the origin of a Cartesian system whose x-axis passes through the shoe hinge H distant a from O. The y-axis is directed generally towards the short lining - whether this system is right- handed or not is irrelevant. The lining is located at angle θm from the x-axis.
The shoe free body is shown at ( b) with the actuation moment M = Pe and the effect of the braked body (drum) contact on the lining expressed by the normal reaction N and the friction force μN in the sense of braked body motion - just like the short translational shoe.
For rotational equilibrium about the hinge to eliminate the as yet unwanted hinge reaction
( v) N = pm A = M / ( a.sin θm - μ ( r - a.cos θm ) )
This is analogous to ( iii) in expressing the essential proportionality between the normal reaction and the actuation - other forces follow from force equilibrium.
This is really all there is to short shoe brake analysis - however it is useful to introduce two artifices to simplify later work
The double delta notation utilises
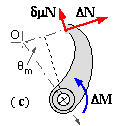
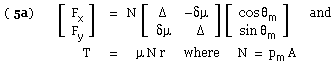
pmis the uniform pressure over the short lining whose contact area is A. The reaction to the torque T is the braking effect exerted by the shoe on the drum.
Taking moments about the hinge for the free body ( d) - [ ( c) serves equally well ] -
( vi) ΔM = a Fy - δT = N [ a ( δμ cosθm + Δ sinθm ) - δμ r ] - and solving for N
( 6a) N = M / [ a sin θm - δΔ μ ( r - a cos θm ) ] - a generalisation of ( v) applicable to all layouts
= M / [ μr ( m - δΔ n ) ] - in which m ≡ 1/μ a/r sin θm and n ≡ 1 - a/r cos θm
are constant dimensionless characteristics of the shoe.
Summarising the analysis steps for a short shoe of known geometry and friction coefficient :
The performance of a single shoe or a complete brake is described by either of two dimensionless figures of merit
The mechanical advantage (or "brake factor"), η
( vii) η = output/input = braking effect/corresponding actuation necessary
The sensitivity, S, reflects the proportional variation of braking torque with fixed actuation as the friction coefficient varies, thus
( viii) S = μ/T . [ ∂T/∂μ ]M = μ/η . dη/dμ
For a single shoe, use of ( 5a), ( 6a) leads to
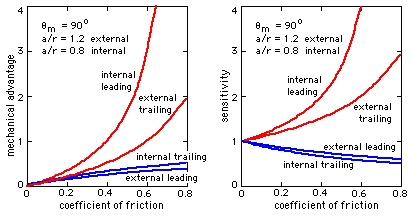
( 8) η = T/M = 1/( m - δΔ n ) and S = m η
These are plotted below for representative short shoes of typical proportions. The curves demonstrate that the same trends apply for both figures of merit, namely
This example analyses a brake with two separately- actuated short shoes, and considers braking torque, sensitivity and bearing loads.
It is now appropriate to examine long shoes - which are more practical than short - before proceeding to look at complete twin shoe brakes.