DANotes: Cylinders: Thin cylinders

CYLINDERS

Cylinders find many applications, two of the most common categories being :

-	fluid containers such as pipes and pressure vessels
-	interference-fitted bearing bushes, sleeves and the like.

Cylinders can act as beams or shafts eg. ( load building blocks which have already been examined ) but in the present context cylinders are loaded primarily by internal and external ( gauge ) pressures p_i and p_o due to adjacent fluids or to contacting cylindrical surfaces.

The following notes examine cylinder safety and derive appropriate design equations. Since the analysis presupposes an elastic material, superposition may be applied if other loading mechanisms such as bending or torsion occur. The treatment ignores end effects and the axial variation of pressures and stresses - so all cross- sections are loaded and stressed identically, and cylinder length is of no consequence. Secondary stresses arising from incompatibility between cylinder and end closure are examined in the context of pressure vessels. 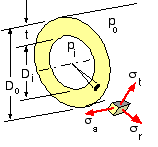cylinder stresses

The stress state in the wall is essentially triaxial and initial analysis gives the principal components without need for resolution :

axial stress, σ_a, sometimes called the longitudinal stress
tangential stress, σ_t, also referred to as the hoop or circumferential stress
radial stress, σ_r . . . . all of which are taken to be positive tensile.

Stresses are identical in cylinders which have geometrically similar cross-sections and which are loaded by the same pressures - absolute size is irrelevant insofar as stresses are concerned. Geometric similarity is expressed by a single ratio between two of the three dimensions - inside diameter (or 'bore') D_i, outside diameter D_o and wall thickness t. Cylinders are usually considered to be either thick - in which stress concentration due to relative curvature is significant - or thin in which stress concentration is negligible. Other differences are :

	Thin	Thick
Limiting proportions (approx)	D_i/t > 20	D_i/t < 25
Analytic treatment	simple approximation	accurate
Statically determinate	yes	no
Stress state	membrane - ie. biaxial	triaxial
Stress - radial, σ_r	zero	varies with radius
- tangential, σ_t	uniform	varies with radius
- axial, σ_a	uniform	uniform

The limiting proportions - the dividing line between thin and thick - is not hard and fast. Whether we choose to treat a particular cylinder as thin or as thick is a matter only of the accuracy we seek from the mathematical model together with the effort we're prepared to expend in solving the model. For example, if in a particular design the thin model results in a cylinder with D_i/t = 7 then we'd either

repeat the calculations using the thick model if an accurate solution was sought, or
accept the result of the thin model knowing that it was in significant error due to the neglect of curvature- induced stress concentration.

We shall address the error associated with the thin cylinders below. The Pressure Vessel Code adopts the latter approach as the Code incorporates large design factors to cater for other imponderables.

Physically, thin cylinders are not suitable when the external fluid pressure is much greater than the internal, unless the cylinder is supported or stiffened against local buckling. We shall not consider thin cylinders with net external pressures sufficient to cause buckling, unless the cylinders are obviously adequately supported as in figure (a) below.

Axial stress

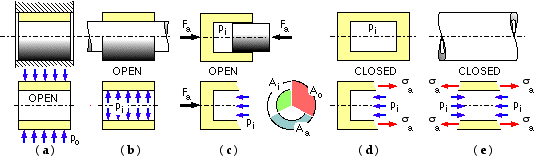
Cylinders are classed as being either :

open - in which there is no axial component of wall stress, or
closed - in which an axial stress must exist to equilibrate the fluid pressure.

Open cylinders are typified by interference-fitted bushes figures (a) and (b) below, in which there are no longitudinal pressures and so no axial stresses.

A fluid container sealed by a piston is open (c) - in this case an external axial force F_a is mandatory for equilibrium of the overall piston-and-cylinder assembly (a bicycle pump is a common example). If A_i is the internal circular area then a free body of either piston or cylinder end (c) must have F_a = p_iA_i and there is no need for axial wall stresses to equilibrate the fluid pressure.

If an axial stress does exist then it is uniform across the cylinder wall, no matter whether the cylinder is thin or thick. The stress may be found easily from equilibrium in the axial direction, aided by a free body viewed in side sectional elevation. Considering the free body of one end of an internally pressurised closed cylinder (d) the fluid pressure resultant p_iA_i is equilibrated by the wall stress resultant σ_aA_a - where the annular wall area is A_a = A_o - A_i in which A_o is the outside circular area.
In the more general case where an external fluid pressure also exists :

( i) σ_a = ( p_iA_i - p_oA_o ) / A_a

A free body (e) of part of a pipe which connects two vessels (not shown) might be thought open, since no ends are evident and the fluid pressure is self-equilibrating across the free body. However each connected vessel acts as a pipe closure, so the pipe is in fact closed and axial stresses must occur.

Thin cylinders

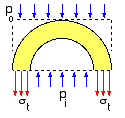The tangential stress is uniform across the wall; so, from equilibrium of the free body : σ_t = ( p_iD_i - p_oD_o ) / 2 t
Since D_i/ t > > 1, this equation with ( i), yields :

( 1) σ_t = Δ_p D_i/ 2 t where Δ_p = p_i - p_o
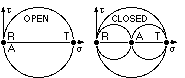
σ_a = Δ_p D_i/ 4 t (CLOSED) or σ_a = 0 (OPEN) Mohr's circles

The radial stress is zero, the tangential stress is always the principal of greatest magnitude, and the axial stress is either zero in the case of open thin cylinders or half the tangential stress in closed thin cylinders. The Mohr's circles thus appear as shown. Derivation of the design equations corresponding to the various failure theories is left as an exercise for the reader :-

( ii) n Δ_p D_i/ t = 2 S_y [ maximum shear stress; distortion energy (open) ]
= ( ⁴/_√3) S_y [ distortion energy (closed) ]
= 2 S_ut [ modified Mohr ]

So much for thin cylinder theory - let us now look at the more realistic but somewhat more elaborate thick cylinder theory . . . .

( ii)	n Δ_p D_i/ t	=	2 S_y	[ maximum shear stress; distortion energy (open) ]
		=	( ⁴/_√3) S_y	[ distortion energy (closed) ]
		=	2 S_ut	[ modified Mohr ]