Assembly Language Programming
PC-Relative Addressing
Register-indirect addressing is simple but suffers from one major problem. How can a 32-bit memory address be loaded into a register in the first place? At first glance, it might seem that a MOV instruction would resolve this issue. However, remember that all ARM instructions are 32 bits long. Some of those bits are needed to identify the instruction's opcode, others are used to indicate the destination register, leaving fewer than 32 bits left for a literal number. So how can this be done?
The ARM uses a special instruction, known as a pseudo-instruction, that does not actually exist. Instead the assembler translates this pseudo-instruction into one or more real instructions. The pseudo-instruction in question is ADR, which loads an address into a destination register.
| copycode | ADR | r1, SOURCEDATA | ; the value of r1 points to the SOURCEDATA location in memory |
| ADR | r2, DESTDATA | ; the value of r2 points to the DESTDATA location in memory | |
| LDR | r0, [r1] | ; load value at memory location pointed to by r1 into r0 (SOURCEDATA) | |
| STR | r0, [r2] | ; store value in r0 to memory location pointed to by r2 (DESTDATA) | |
| . | |||
| SOURCEDATA | . | ; source of data | |
| . | |||
| DESTDATA | . | ; destination for the data |
PC relative addressing in action
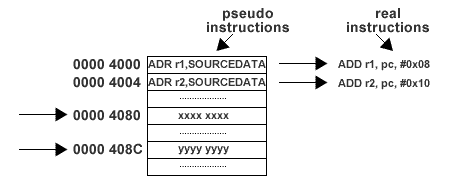
The trick with the ADR instruction relies on the fact that in most cases, the current value of the Program Counter (r15) will normally be "close" to the intended memory address location. Thus an ADR instruction is translated into one or more instructions that can add a constant value to or subtract a constant value from the current value of the Program Counter and place the result in the destination register specified by the original ADR instruction.
This addressing mode is called PC-relative addressing. The constant value is known as the PC-relative offset. It can be calculated by the formula below:
PC-relative offset = desired address - (Program Counter value + 8)
The +8 in the formula is a consequence of how the ARM processes instructions using "pipeline" techniques, but for the purposes of this course, we need merely note the presence of the +8.
